#執筆中/行列式の導出/ソース

行列式の導出

行列式の定義を見ると，どうしてこのような式を考え付いたのか想像しにくいですね．行列式を使わずに連立１次方程式を解いて，行列式の導出を試みましょう．

３元連立１次方程式

一般の場合は式が複雑で考えにくいので，まず

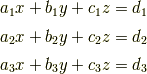
$a_1 x + b_1 y + c_1 z = d_1 \\a_2 x + b_2 y + c_2 z = d_2 \\a_3 x + b_3 y + c_3 z = d_3$

について考えましょう．|9dd4e461268c8034f5c8564e155c67a6|を求めるために

System Message: WARNING/2 (<stdin>, line 25); backlink

Inline substitution_reference start-string without end-string.

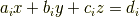
の辺々に 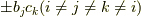$\pm b_j c_k (i \neq j \neq k \neq i)$ をかけた

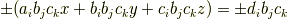
$\pm (a_i b_j c_k x + b_i b_j c_k y + c_i b_j c_k z) = \pm d_i b_j c_k$

に対して，例えば

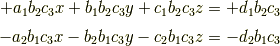
$+ a_1 b_2 c_3 x + b_1 b_2 c_3 y + c_1 b_2 c_3 z = + d_1 b_2 c_3 \\- a_2 b_1 c_3 x - b_2 b_1 c_3 y - c_2 b_1 c_3 z = - d_2 b_1 c_3$

を辺々加算すると|415290769594460e2e485922904f345d|の係数が

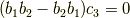
となります．また，

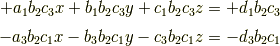
$+ a_1 b_2 c_3 x + b_1 b_2 c_3 y + c_1 b_2 c_3 z = + d_1 b_2 c_3 \\- a_3 b_2 c_1 x - b_3 b_2 c_1 y - c_3 b_2 c_1 z = - d_3 b_2 c_1$

System Message: WARNING/2 (<stdin>, line 75); backlink

Inline substitution_reference start-string without end-string.

System Message: WARNING/2 (<stdin>, line 75); backlink

Inline substitution_reference start-string without end-string.

System Message: WARNING/2 (<stdin>, line 75); backlink

Inline substitution_reference start-string without end-string.

System Message: WARNING/2 (<stdin>, line 75); backlink

Inline substitution_reference start-string without end-string.

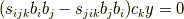
$(s_{ijk} b_i b_j - s_{jik} b_j b_i) c_k y = 0$

|7008774ba2a3c07021d61c54294cb0ef|ならば

System Message: WARNING/2 (<stdin>, line 86); backlink

Inline substitution_reference start-string without end-string.

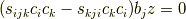
$(s_{ijk} c_i c_k - s_{kji} c_k c_i) b_j z = 0$

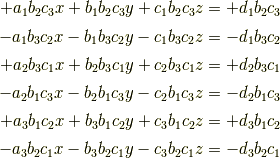
$+ a_1 b_2 c_3 x + b_1 b_2 c_3 y + c_1 b_2 c_3 z = + d_1 b_2 c_3 \\- a_1 b_3 c_2 x - b_1 b_3 c_2 y - c_1 b_3 c_2 z = - d_1 b_3 c_2 \\+ a_2 b_3 c_1 x + b_2 b_3 c_1 y + c_2 b_3 c_1 z = + d_2 b_3 c_1 \\- a_2 b_1 c_3 x - b_2 b_1 c_3 y - c_2 b_1 c_3 z = - d_2 b_1 c_3 \\+ a_3 b_1 c_2 x + b_3 b_1 c_2 y + c_3 b_1 c_2 z = + d_3 b_1 c_2 \\- a_3 b_2 c_1 x - b_3 b_2 c_1 y - c_3 b_2 c_1 z = - d_3 b_2 c_1$

が得られ，総和をとると|415290769594460e2e485922904f345d|，|fbade9e36a3f36d3d676c1b808451dd7|の係数がいずれも 0 になることが分かります．

System Message: WARNING/2 (<stdin>, line 107); backlink

Inline substitution_reference start-string without end-string.

置換による表現

System Message: WARNING/2 (<stdin>, line 115); backlink

Inline substitution_reference start-string without end-string.

System Message: WARNING/2 (<stdin>, line 115); backlink

Inline substitution_reference start-string without end-string.

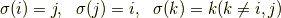
$\sigma(i) = j,~~ \sigma(j) = i,~~\sigma(k) = k (k \neq i, j)$

ですが，これを|5e33e4b364139e91328f66f0e78efc2c|とかきます．任意の置換は互換の繰り返し（合成写像）で表現できます．表現の仕方はいろいろありますが，置換を表現するのに必要な互換の数は偶数か奇数かは変わりません．互換の数が偶数の置換を偶置換，奇数の置換を奇置換といい，置換の符号を

Error : LaTeX command contains irregal 2bytes character(s).

System Message: WARNING/2 (<stdin>, line 140); backlink

Inline substitution_reference start-string without end-string.

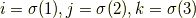
$i = \sigma(1), j = \sigma(2), k = \sigma(3)$

と表現でき，置換を用いると|7b8b965ad4bca0e41ab51de7b31363a1|元連立１次方程式への拡張が容易になります．

一般化準備として，まず

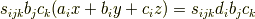
$s_{ijk} b_j c_k (a_i x + b_i y + c_i z) = s_{ijk} d_i b_j c_k$

を置換を用いて書き換えましょう．|80fed756c8358e6a19850beb8178f9bd|とし

System Message: WARNING/2 (<stdin>, line 162); backlink

Inline substitution_reference start-string without end-string.

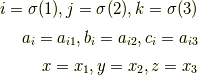
$i = \sigma(1), j = \sigma(2), k = \sigma(3) \\a_i = a_{i1}, b_i = a_{i2}, c_i = a_{i3} \\x = x_1, y = x_2, z = x_3$

を代入した

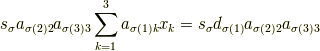
$s_\sigma a_{\sigma(2)2} a_{\sigma(3)3} \sum_{k=1}^3 a_{\sigma(1)k} x_k= s_\sigma d_{\sigma(1)} a_{\sigma(2)2} a_{\sigma(3)3}$

が|aa687da0086c1ea060a8838e24611319|を求める式であることに注意．|8732099f74d777a67257cb2f04ead3d8|を求めるときの式は

System Message: WARNING/2 (<stdin>, line 182); backlink

Inline substitution_reference start-string without end-string.

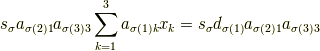
$s_\sigma a_{\sigma(2)1} a_{\sigma(3)3} \sum_{k=1}^3 a_{\sigma(1)k} x_k= s_\sigma d_{\sigma(1)} a_{\sigma(2)1} a_{\sigma(3)3}$

あるいは|a2ab7d71a0f07f388ff823293c147d21|を変更した

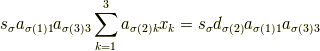
$s_\sigma a_{\sigma(1)1} a_{\sigma(3)3} \sum_{k=1}^3 a_{\sigma(2)k} x_k= s_\sigma d_{\sigma(2)} a_{\sigma(1)1} a_{\sigma(3)3}$

であり，|1f89889020cdc84d9e1c35237cb62f65|を求める式は

System Message: WARNING/2 (<stdin>, line 202); backlink

Inline substitution_reference start-string without end-string.

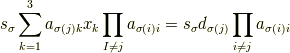
$s_\sigma \sum_{k=1}^3 a_{\sigma(j)k} x_k \prod_{I \neq j} a_{\sigma(i)i}= s_\sigma d_{\sigma(j)} \prod_{i \neq j} a_{\sigma(i)i}$

System Message: WARNING/2 (<stdin>, line 212); backlink

Inline substitution_reference start-string without end-string.

一般化

System Message: WARNING/2 (<stdin>, line 222); backlink

Inline substitution_reference start-string without end-string.

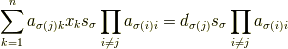
$\sum_{k=1}^n a_{\sigma(j)k} x_k s_\sigma \prod_{i \neq j} a_{\sigma(i) i}= d_{\sigma(j)} s_\sigma \prod_{i \neq j} a_{\sigma(i) i}$

の|a2ab7d71a0f07f388ff823293c147d21|についての総和をとると，|945315e9d656ad23442dd758248b758e|の係数は

System Message: WARNING/2 (<stdin>, line 233); backlink

Inline substitution_reference start-string without end-string.

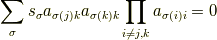
$\sum_\sigma s_\sigma a_{\sigma(j) k} a_{\sigma(k) k}\prod_{i \neq j, k} a_{\sigma(i) i} = 0$

System Message: WARNING/2 (<stdin>, line 243); backlink

Inline substitution_reference start-string without end-string.

System Message: WARNING/2 (<stdin>, line 243); backlink

Inline substitution_reference start-string without end-string.

System Message: WARNING/2 (<stdin>, line 243); backlink

Inline substitution_reference start-string without end-string.

System Message: WARNING/2 (<stdin>, line 243); backlink

Inline substitution_reference start-string without end-string.

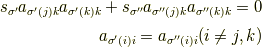
$s_{\sigma'} a_{\sigma'(j)k} a_{\sigma'(k)k} + s_{\sigma''} a_{\sigma''(j)k} a_{\sigma''(k)k} = 0 \\a_{\sigma'(i)i} = a_{\sigma''(i)i} (i \neq j, k)$

となることで証明できます．

補遺

発見的に考えるには対象を簡単化して見易い記号を使うこと．最初から

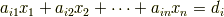
$a_{i1} x_1 + a_{i2} x_2 + \cdots + a_{in} x_n = d_i$

で考えようとすると無用な複雑さで思考が妨げられます．

(2)「３元連立１次方程式」では|6ad43a65711267334c0d010419163143| に 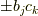$\pm b_j c_k$ を天下り的にかけましたが，

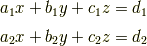
$a_1 x + b_1 y + c_1 z = d_1 \\a_2 x + b_2 y + c_2 z = d_2$

から|fbade9e36a3f36d3d676c1b808451dd7|を消去すると

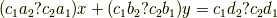
(c_1 a_2 ?c_2 a_1) x + (c_1 b_2 ? c_2 b_1) y = c_1 d_2 ? c_2 d_1

が得られ，同様に

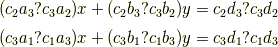
$(c_2 a_3 ?c_3 a_2) x + (c_2 b_3 ? c_3 b_2) y = c_2 d_3 ? c_3 d_2 \\(c_3 a_1 ?c_1 a_3) x + (c_3 b_1 ? c_1 b_3) y = c_3 d_1 ? c_1 d_3$

も成立するので，|415290769594460e2e485922904f345d|の係数に注目して

System Message: WARNING/2 (<stdin>, line 308); backlink

Inline substitution_reference start-string without end-string.

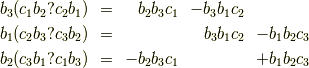
$\begin{array}{rrrrr}b_3 (c_1 b_2 ? c_2 b_1) & = & b_2 b_3 c_1 & - b_3 b_1 c_2 & \\b_1 (c_2 b_3 ? c_3 b_2) & = & & b_3 b_1 c_2 & - b_1 b_2 c_3 \\b_2 (c_3 b_1 ? c_1 b_3) & = & - b_2 b_3 c_1 & & + b_1 b_2 c_3 \\\end{array}$

から，加重加算によって|415290769594460e2e485922904f345d|の係数をにできることが分かります．行列式で表すと

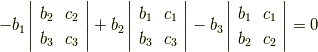
$- b_1 \left| \begin{array}{cc} b_2 & c_2 \\ b_3 & c_3 \end{array} \right| + b_2 \left| \begin{array}{cc} b_1 & c_1 \\ b_3 & c_3 \end{array} \right|- b_3 \left| \begin{array}{cc} b_1 & c_1 \\ b_2 & c_2 \end{array} \right|= 0$

です．

連立1次方程式

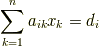
$\sum_{k=1}^n a_{ik} x_k = d_i$

の解|1f89889020cdc84d9e1c35237cb62f65|は

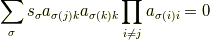
$> ! File ended while scanning use of \align*.$ $\sum_\sigma s_\sigma a_{\sigma(j)k} a_{\sigma(k)k} \prod_{i \neq j} a_{\sigma(i)i} = 0$ > ! Missing } inserted.

から|1f89889020cdc84d9e1c35237cb62f65|の係数が0でなければ一意に定まります．

System Message: WARNING/2 (<stdin>, line 368); backlink

Inline substitution_reference start-string without end-string.

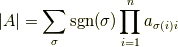
$|A| = \sum_\sigma {\rm sgn}(\sigma) \prod_{i=1}^n a_{\sigma(i) i}$

System Message: WARNING/2 (<stdin>, line 378); backlink

Inline substitution_reference start-string without end-string.

あとがき

Docutils System Messages

System Message: ERROR/3 (<stdin>, line 96); backlink

Undefined substitution referenced: "39ea6ef2598040e5f573f664f028a80b|を初期値として符号|f8d6856ce7090fa6159170fbc855477e|を|2acdabd94f93ff7d4c45f49f5bbea51e".

参考文献

[home] [初等代数] [ページの先頭]