包絡線について
包絡線について
リモコン さんの書込 (2008/12/07(Sun) 22:26)
初めまして現在高校二年生のHN:リモコンです 「物理のかぎしっぽ」は自分の好奇心をくすぐらせる記事ばかりでいつも利用させてもらっています. そこで,数学-雑多な豆知識-包絡線 の記事の中の「陰関数の包絡線」
という部分で
df/dc=0 は曲線群fに(包絡線が)接するということを表す
という部分がありますが,この式がなぜ曲線群fに(包絡線が)接するということを表すのか,自分力では方程式からイメージすることが出来ません.
説明頂けたらお願いします.
Re: 包絡線について
mNeji さんのレス (2008/12/08(Mon) 02:00)
リモコンさん,初めまして.
間違っているかも知れませんが,自分なりの考え方を示します.
今,点(x,y)を考えます.この点がCをパラメータとする曲線群;

に対する包絡線(エンヴェロープ)にも含まれているとしても,その関数,
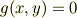
はパラメタCには依存しない筈です,言い換えれば,包絡線の中では,
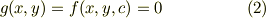
点  の近傍点 |7215ee9c7d9dc229d2921a40e899ec5f|(x+\delta x,y+\delta x)|7215ee9c7d9dc229d2921a40e899ec5f| はパラメータ,
の近傍点 |7215ee9c7d9dc229d2921a40e899ec5f|(x+\delta x,y+\delta x)|7215ee9c7d9dc229d2921a40e899ec5f| はパラメータ, 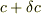 の曲線群に属し,かつほう包絡線上にあるとします.
の曲線群に属し,かつほう包絡線上にあるとします.
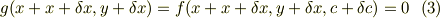
以上の式が同時に成立するので,「(3)-(1)」とから
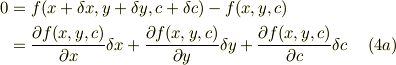
となります.同様に
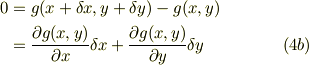
ここで,式(2)に注意して,式(4a,b)を辺々引くと
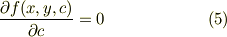
となる.
#この式(5)と式(1)よりパラメータCを消去したものが式(3)の左辺,包絡線の方程式になるのだと思います.
包絡線の傾きは,(5)より
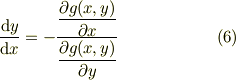
となります.
とゆう感じでしょうかね.なんか廻りくどすぎますが....やはり媒介変数を持って来る方が自然でしょうか?
Re: 包絡線について
DIO さんのレス (2008/12/08(Mon) 20:35)
過去ログに同様の質問がありました.とても参考になると思います.
ttp://hooktail.maxwell.jp/bbslog/17929.html
Re: 包絡線について
anon さんのレス (2008/12/09(Tue) 09:51)
上で紹介された過去ログにもコメントを書いていた者です. 此度のリモコンさんは高校二年生ということで, あの過去ログの説明だとわからない部分もあるんじゃないかと思います. 何かあればここで訊いてみて下さい.
話変わって,mNejiさんの(2)の式についてわからない点があったのですが, 「包絡線の中では,(2)」というのは, 「(x,y)が包絡線上の点であれば,任意のcに対して(2)が成り立つ」 という意図でしょうか?
Re: 包絡線について
mNeji さんのレス (2008/12/09(Tue) 10:44)
anonさん,ご意見をくださり感謝します.
最近,関数の全微分を考える事が多くて,つい調子に乗って書き込んだものの,自分でも「上手く説明できず」,気になっているところです.
ご指摘の;
>「包絡線の中では,(2)」というのは, >「(x,y)が包絡線上の点であれば,任意のcに対して(2)が成り立つ」
部分も上手く書けていないですね.
この式, 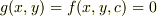 ,で言いたいのは,
,で言いたいのは,
『曲線群のうち,あるパラメータ「c」で与えられる曲線 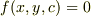 が包絡線
が包絡線 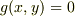 と交差したていれば,その座標
と交差したていれば,その座標 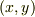 は連立方程式;
は連立方程式;
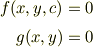
の解になる.』
なのですが,自分でも表現が不十分だと感じます.お恥ずかしい事に,陰関数の取り扱い方を理解出来ていない様です.
言葉で表現出来ないので,絵にしてみます.
- <pre>
- y
↑ | | | | | f(x,y,c+dc)=0 | *g(x,y)=0 | | * | | * Y+dY ・ ・ | * (2) 微小変位(dX,dY)を与えた点が | f(x,y,c)=0 *やはり交点ならば,dcが決まる. | * g(X+dX,Y+dY)=0 -> f(X+dX,Y+dY,c+dc)=0 || * | | *
Y・ ・
| (1) cを与えると,交点(X,Y)が決まる. | f(X,Y,c)=0 -> g(X,Y)=0 | +ーーーーーーーー・ーーーーーー・ーーーーーーー→x O X X+dX </pre>
Re: 包絡線について
mNeji さんのレス (2008/12/09(Tue) 16:44)
リモコンさん,
私の論議は,「包絡線の条件」を見いだす視点が欠けていると思い当たりました.現在検討中ですが,直ぐに理解出来るか不明です.
すでにanonさんのご説明があるようですので,そちらに沿って勉強されるのをお勧めします.
余計な話で混乱させて,ご免なさい.
Re: 包絡線について
anon さんのレス (2008/12/11(Thu) 20:32)
元質問者のリモコンさんからはまだ音沙汰がないようですが, それは置いておいて,mNejiさんのコメントについてです.
No.22445 のご説明で私が理解したつもりのものは,こういうことです.
「(x,y)を包絡線上の点とすると,曲線群の中に(x,y)を通る曲線があって, その曲線を表すパラメータをcとすれば, f(x,y,c)=0 および g(x,y)=0 がともに成り立っている」...(*)
ただ,この二つの等式が,
あくまでも包絡線上の点(x,y)と対応するcに対して成り立つ等式であることに
注意が必要になると思います.
この二つの等式をつなげて g(x,y)=f(x,y,c)=0 と書いてしまうと,
g(x,y)=f(x,y,c) が x と y についての関数としての等式のような気がしてしまいます.
そうして, 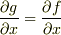 などが成り立つような気がしますけれども,
実はこうなる保証はないのですよね.
などが成り立つような気がしますけれども,
実はこうなる保証はないのですよね.
ですから,No.22436 の (4a) および (4b) は確かに成り立つと思いますが, それらを辺々引いても (5) が導かれないのだと思います.
とはいってもよく考えがまとまらないまま書いていますので, 考え違いがあるかもしれません. どなたでもフォローアップをよろしくお願いいたします.
Re: 包絡線について
mNeji さんのレス (2008/12/12(Fri) 00:39)
anonさん,ご検討有り難うございます.
この手の問題を,自分なりに解こうとしたのは初めてで,朦朧としています.
特に判らないのが,「包絡線」というのは,曲線群の内で,c=一定編面の見た時に「縁」となるような部分が連なったものだろうと思うのですが,それと 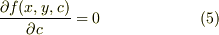 とがイメージ的に一致しないので困惑しています.
とがイメージ的に一致しないので困惑しています.
>あくまでも包絡線上の点(x,y)と対応するcに対して成り立つ等式であることに 注意が必要になると思います.
これは判る気がします.リダンダントに書けば,包絡線上の(x,y)は「cの関数」;
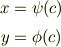
であり,これらは同時に,
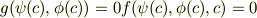
を満たすのですね.
「分るようで,分らない」という感じで,じれています(笑い).
幾何学的にスマートな解釈をご存知でしたら,お先にお願いします.
Re: 包絡線について
mNeji さんのレス (2008/12/12(Fri) 11:57)
これまでの書き込みは,細切れになっていて,結論も明白でないので,書き直しさせて戴きます.
さて,一般に,陰関数 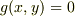 の接線の傾きは;
の接線の傾きは;
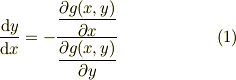
で与えられます.
そこで与えられた曲線群

の中で,パラメータ「c=一定」の曲線に付いての接線の傾きを考えれば,式(1)と同じ様に,
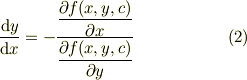
で与えられます.この関係は,この曲線群の包絡線の有無とは別にいつでも成立します.
ところが,式(2)の内で,包絡線となる座標(X,Y)とすると,当然,

を満たします.
次に包絡線の位置が微小変化した場合を考えます.座標(X,Y)から座標(X+dX,Y+dY)への変化を考えます.この時に,大切なのは,同時にパラメータ(c)も(c+dc)の変化をする必要があります.もしパラメータ(c)が一定ならば,式(2)と同じで,包絡線になり得ないからです.従って,式(3)と同時に;
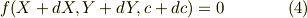
も満たす必要があります.
式(4)と式(3)との差分を取ると;
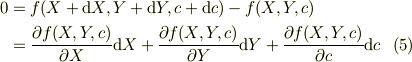
これを 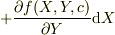 で割って整理すると,
で割って整理すると,
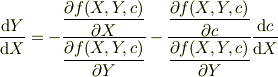
ここで,この傾きの式は,式(2)で,(x,y)を(X,Y)とした時の傾きとも一致する必要がある.この右辺の第2項は常時ゼロとなる必要がある.ところが 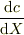 は,包絡線の意味から常時ゼロにならない.したがって,包絡線が接線となる為には,
は,包絡線の意味から常時ゼロにならない.したがって,包絡線が接線となる為には,
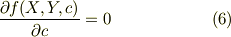
が必要になる.
逆に,式(2)の包絡線があれば,それは,式(2)と式(6)からパラメータcを消去して得る事ができる.
Re: 包絡線について
toorisugari no Hiro さんのレス (2008/12/12(Fri) 12:26)
提案なのですけど,包絡線は取り扱いが難しいので,包絡「点」で考えてみてはどうでしょう.
つまり,以下のような問題をどう説明するかです.
「
 を正の実数,
を正の実数,  を実数として,
を実数として,  の方程式
の方程式
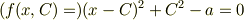
の解を考える. 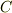 を任意に変化させたとき,方程式を満たす
を任意に変化させたとき,方程式を満たす  の最大値と最小値をもとめよ.
」
の最大値と最小値をもとめよ.
」
いろいろなやり方があると思います.
(1) 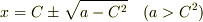 を満たす
を満たす  の最大値と最小値をもとめる.
(2)
の最大値と最小値をもとめる.
(2) 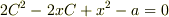 を満たす実数
を満たす実数 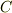 が存在するための
が存在するための  の条件.
(3)
の条件.
(3) 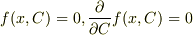 から
から 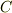 を消去する.
を消去する.
(3)をうまく説明できればいいのですよね.
# 追記11/18 : anonさんのご指摘により間違いを正しました.
Re: 包絡線について
リモコン さんのレス (2008/12/14(Sun) 22:42)
投稿した私がなかなか返信出来なくてすみませんでした.
高校での生活がとても忙しく掲示板に返信出来ませんでした.
みなさんのご回答を見てみて,何となく包絡線の方程式のイメージがつかめました.
その中で,「陰関数接線の微分係数dy/dx」がfのx,yについての偏微分で表されることを説明するため,「全微分」について,もう少し自分で学んでみなければならないことを自覚しました...
Re: 包絡線について
mNeji さんのレス (2008/12/15(Mon) 00:08)
リモコンさん,
>高校での生活がとても忙しく掲示板に返信出来ませんでした.
そのくらい忙しいくらいが善いかも知れませんね.
>「全微分」について,もう少し自分で学んでみなければならないことを自覚しました...
偏微分は普通の微分と記号が違うので驚きますが,大学では物理や数学で教えられるので,あまり気にしないでください.夏休みに気が向いたら勉強して,判らなければ,ここに質問すると優しい解説が頂けると思いますよ.
Re: 包絡線について
anon さんのレス (2008/12/18(Thu) 12:52)
まず,リモコン さんへ. No.22440 で DIO さんに紹介していただいた過去ログはご覧いただけたでしょうか. もしまだならちょっと読んでみてくださいね. mNeji さんが「幾何学的にスマートな解釈を...」と仰っていましたけれども, 私がスマートだと思う解釈が,その過去ログにありますので. (過去ログのほうですが,今読み直してみると一部の数式が飛んでしまっているようですが???)
ここからはみなさんへ. No.22456 で toorisugari no Hiro さんのお話にある「包絡点」の (3) の問題は, 上の過去ログでの話を一次元下げると説明できますよね. (Hiroさんには過去ログのときも声をかけていただいていましたね.お返事もせず失礼いたしました.) No.22456 の (1) の数式ですが,ルートの中身は引き算が逆のようですね.その後の不等式もですが. ところで,この Hiroさんの問題は, x-C 平面の中の傾いた楕円を想像しないと理解できなさそうですから, 高校生には少し難しいかもしれませんね.(と,ちょっとヒントを...)
No.22455 の mNeji さんのお話は,ちょっと把握し切れていません. 個々の数式がどういう状況で成立するのかがクリアに見えてこない感じです. 例えば,「常時ゼロとなる」の“常時”とは(X,Y,c)が包絡線上の点として 実現している限りのことなのか,そうでなくとも良いのか, といったあたりなどです. 私の理解が足りていないようです.
最後に,リモコン さんへ. mNeji さんも仰っていますが, 考えてみてわからなければ,またなんでも書き込んでみるとよいですよ. では,勉強がんばってください.
Re: 包絡線について
mNeji さんのレス (2008/12/18(Thu) 15:12)
anonさん,
>私がスマートだと思う解釈が,その過去ログにありますので. >(過去ログのほうですが,今読み直してみると一部の数式が飛んでしまっているようですが???)
ここで言及されているのは
「17929 包絡線 Wilhelm C. 2007/09/22(Sat) 17:33」
のなかのご発言でしょうか?もしそうだとすれば,DIO さんのご紹介があった時点で拝見しましたが,私には理解出来ませんでした.しかし,私は数学が苦手なので,当方の理解力が無い為と思っていました.
【追加説明2008-12-19 05:00頃】
もしも,ご説明中の数式が消失しているとするならば,是非とも数式を復元していただけませんか?それを見て,勉強させて頂きたいものです.
#過去の論議の中でも,重要な論議が全く見えなく成っている事が結構在ります.残念ですが,発言者側で修復するしか無いのだろうと思っています.
>個々の数式がどういう状況で成立するのかがクリアに見えてこない感じです. >例えば,「常時ゼロとなる」の“常時”とは(X,Y,c)が包絡線上の点として >実現している限りのことなのか,そうでなくとも良いのか, >といったあたりなどです.
自分のイメージとしては出来た感じですが,数学的な明瞭さを得ているとは思えません.是非とも,数学の不得意な私に,ナイーブな数学の言葉でイメージし易く,しかもクリアに表現戴けると幸いです.
Re: 包絡線について
toorisugari no Hiro さんのレス (2008/12/18(Thu) 15:50)
> No.22456 の (1) の数式ですが,ルートの中身は引き算が逆のようですね.その後の不等式もですが.
わっ.恥ずかしい.ご指摘ありがとうございます.
> この Hiroさんの問題は,x-C 平面の中の傾いた楕円を想像しないと理解できなさそうですから,高校生には少し難しいかもしれませんね.(と,ちょっとヒントを...)
うーむ,わかりやすい図形にすると解が自明になるんですよね...
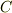 の境界の処理と複数の包絡点が存在することがいやですが,
「
の境界の処理と複数の包絡点が存在することがいやですが,
「
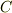 を負でない実数として任意に変化させたとき,式
を負でない実数として任意に変化させたとき,式
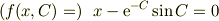
を満たす  の最大値と最小値をもとめよ.ただし,解には定数
の最大値と最小値をもとめよ.ただし,解には定数 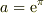 を用いて良い.
」
を用いて良い.
」
ならどうでしょう.
# このグラフは高校生には難しいかな?かといって 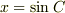 にすると自明だし.
にすると自明だし.
Re: 包絡線について
anon さんのレス (2008/12/19(Fri) 09:58)
mNeji さんへ
私の発言はもともとTeXによる数式を埋め込んではいないので,抜けているところはありません. 抜けてると思ったのは,その過去ログにある Hiro さんの解説のところで, 「delta c を微小量として(改行)をみたす交点 (x_c,y_c) をとびとびの」 「delta c の1次のテーラー展開(数式二本)から(改行)がえられますが,この条件(b)は」 という部分があるのですが, (改行)のところにはいずれも数式があったのではないかと思えたからでした. 取り急ぎ,この点だけで失礼いたします.
Hiro さんへ
> うーむ,わかりやすい図形にすると解が自明になるんですよね...
なじみのない事柄についての一般論を考えるのですから, 自明なものでいいのじゃないかとも思います. その次にいろいろな例で考えることにして.
# ところで,念のため. # 上で「(と,ちょっとヒントを...)」と書いたのは,リモコンさんに対して, # 「Hiro さんの式は楕円を表しているんですよ」というヒントを出したつもりで書いていました.
Re: 包絡線について
toorisugari no Hiro さんのレス (2008/12/19(Fri) 11:58)
> 抜けてると思ったのは,その過去ログにある Hiro さんの解説のところで,
たぶん,過去ログ化のエンコーディング段階で落ちたのでしょうね. その後にanonさんの解説が無傷であるので,復元は不要とほっておきましたが,話の筋上,復元した方がいいのかな?
記憶に頼って復元します,と思いましたが,書き直したくなったので,書き直したものを載せます.
「
包絡線は 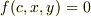 の
の  を少しづつずらした曲線を重ねたときの交点をつなげたものと考えられます.
を少しづつずらした曲線を重ねたときの交点をつなげたものと考えられます.
つまり 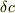 を微小量として
を微小量として
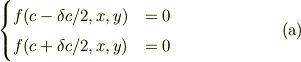
をみたす交点 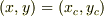 をとびとびの
をとびとびの 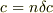 (
(  :整数)に対してつなげたものが近似包絡線です.
:整数)に対してつなげたものが近似包絡線です. 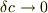 で近似包絡線は包絡線に一致します.
で近似包絡線は包絡線に一致します.
さて,微分の定義
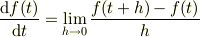
から十分小さい 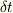 に関して
に関して
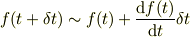
という近似式(1次のテーラー展開)が得られます.
これを使って条件(a)において  を変数と観て,
を変数と観て, 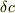 の1次で展開すると
の1次で展開すると
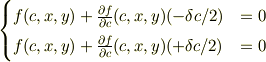
(  だけを変数と観るという意味で,偏微分
だけを変数と観るという意味で,偏微分 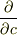 を使っています.)
が得られるので,これより,
を使っています.)
が得られるので,これより,
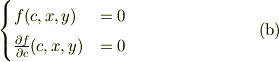
がえられます.
この条件(b)は条件(a)と 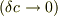 において等価です.
つまり,条件(b)を満たす
において等価です.
つまり,条件(b)を満たす 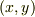 の集合が包絡線になります.
の集合が包絡線になります.
なお,(b)の第2式は  が変化しても動かない点という解釈もできます.
」
が変化しても動かない点という解釈もできます.
」
> # ところで,念のため. わはは.すっかり誤解してました.