包絡線

包絡線

Wilhelm C. さんの書込 (2007/09/22(Sat) 17:33)

はじめまして．包絡線の求め方について質問させていただきます． 本文には，

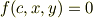
f(c,x,y)=0

の包絡線は，

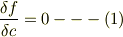
\frac{\delta f}{\delta c}=0 ---(1)

かつ

f=0 ---(2)

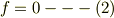
の解として求められることになっています．そしてその理由として(1)は接線の傾きが同じであることから，(2)は同じ点を通ることから当然であるという説明がなされていますが，その説明では関数fは直線と包絡線の差をあらわす関数ということになります．このあたりがよくわからないのでご説明よろしくお願いいたします．

Re: 包絡線

toorisugari no Hiro さんのレス (2007/09/25(Tue) 18:06)

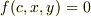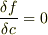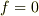> 本文には， > f(c,x,y)=0 > の包絡線は， > \frac{\delta f}{\delta c}=0 ---(1) > かつ > f=0 ---(2) > の解として求められることになっています．

この記事

についての質問ですね．

(1)(2)から包絡線が求まる理由ですが，手近な所で解説が見あたらないので，余り上手な説明ではありませんが，以下のように考えたらどうでしょう．

包絡線は 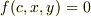f(c,x,y)=0 の c を少しづつずらした曲線を重ねたときの交点をつなげたものと考えられます．

つまり 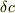\delta c を微小量として

をみたす交点 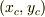(x_{c},y_{c}) をとびとびの 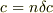c=n \delta c に対してつなげたものが(近似)包絡線です．

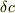\delta c の1次のテーラー展開

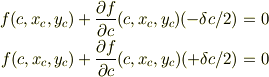
f(c,x_{c},y_{c})+\frac{\partial f}{\partial c}(c,x_{c},y_{c}) (-\delta c /2)&=0\\f(c,x_{c},y_{c})+\frac{\partial f}{\partial c}(c,x_{c},y_{c}) (+\delta c /2)&=0

から

がえられますが，この条件(b)は条件(a)と( 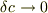\delta c \to 0 )において等価です． (b)の第2式は c が変化しても動かない点という解釈もできます．

Re: 包絡線

anon さんのレス (2007/09/26(Wed) 11:25)

Wilhelm C.さんのおっしゃる，「関数fは直線と包絡線の差をあらわす関数ということになる」というのがどういうことなのかよく分からないのですが，包絡線についてちょっと別の見方も紹介してみます．

c をパラメータとする x-y 平面内の曲線群を， x-y-c 空間内の曲面と見なすのも有効です．

この曲面の c 軸方向を潰す（x-y平面に押しつぶすようなイメージです．計算上は，方程式から変数 c を消去することに対応します．）と x-y 平面内のある領域となりますが，その領域の境界線が元の曲線群の包絡線になっているはずです．

この様子が了解できれば，この押しつぶしによって包絡線に移るはずの x-y-c 空間内の点が，元の曲面上で法線が水平方向を向いているような点であることも容易に想像できるでしょう．

そのような点は，曲面上の点（f=0）であって，法線ベクトルの c 方向成分が 0（f_c=0）というように特徴付けられます．この条件から得られるものは x-y-c 空間内の曲面に張り付いたある曲線になっていて，この曲線を x-y 平面に押しつぶす（つまり方程式から c を消去する）と包絡線が得られます．

Re: 包絡線

toorisugari no Hiro さんのレス (2007/09/26(Wed) 15:34)

anonさん，followありがとうございます．

なるほど，次元をあげて考えるのですね．明瞭な議論，参考になりました．

Re: 包絡線

Joh さんのレス (2007/09/26(Wed) 21:20)

toorisugari no Hiroさん，anonさん，色々な解説ありがとうございました． この記事はかなり昔に書いたものですが，今見ると，あまりよく分かっていない 部分もあります．暇をみて，改訂したいと思います． どうもありがとうございました．