ぼや さんの書込 (2008/07/12(Sat) 19:48)

問題1：平均の速さと瞬間的な速さの違いを，おのおの定義式を用いて，さらにそれぞれの幾何学的意味を説明せよ．

問題2：人が5秒の間に7m歩いた．この間の平均の速さを求めよ．また，この速さは時速に換算すると，時速何kmとなるか．

問題3：15[m/s]の速さで直線状を走っていた自動車がブレーキをかけ，その後一定の加速度で運動し3[s]後に止まった．次の設問に答えよ． (a)ブレーキをかけた後の加速度を求めよ． (b)ブレーキをかけてから自動車が止まるまで，自動車は何[m]進んだか．

問題4：等速度vでx軸上を運動する質点が，時刻tにおける座標がx=x0＋vtと表されるとき，これからΔx/Δt=vを導け．また，xがtの関数として x=1/2αt^2＋v0t＋x0 で与えられるとき(α,v0,x0は定数)，速度vを計算せよ．

問題5：一直線上を自動車が時速30[km]で運動しているとする．時刻0からt分後に自動車が進んだ距離をs[m]としたとき，tとsとの間にはどんな関係が成り立つか・次の?〜?のうちから，正しいものを1つ選べ． ?s=100t?s=200t?s=500t?s=800t

問題6：Aベクトル=(−1,2,−3)のとき，4Aベクトルを求めよ．

問題7：Aベクトル=(1,2,3,)，Bベクトル=(−4,3,1)のとき2Aベクトル＋3Bベクトルはどのように表されるか．

問題8：2つのベクトルに対し Ax=Bx，Ay=By,Az=Bz が成立するとき，ベクトルAベクトル=(Ax,Ay,Az)とBベクトル=(Bx,By,Bz)は互いに等しいといいAベクトル=Bベクトルであると定義する．以上の定義を使い，ベクトルAベクトルを平行移動してしたベクトルはもともとのAベクトルに等しいことを示せ．

問題9：ベクトルAベクトルがx,y,z軸となす角度の余弦をα,β,γとすれば α=Ax/A,β=Ay/A，γ=Az/A となる．α,β,γを方向余弦という．方向余弦に対しα^2＋β^2＋γ^2=1の関係が成り立つことを示せ．

問題10：3次元空間を運動する質点のx,y,z座標が x=αt,y=βt^2,z=γt^3(α,β,γ：定数) と表されるとする．質点の速度，加速度を求めよ．

上記の問題の解答を過程も含めて教えてくれないでしょうか？ 問題6は多分(−4,8,−12)だと思うのですが・・・

toorisugari no Hiro さんのレス (2008/07/12(Sat) 21:33)

No.20503( http://hooktail.maxwell.jp/bbslog/20503.html )と相変わらず同じパターンですね． 大量の問題の丸投げでは，好印象をもたれませんよ．

「よい質問のしかた」

• http://hooktail.maxwell.jp/yybbs/howToQuestion/index.html

を精読しましょう． あと，Pepperさんが最後に書かれたレスもよく読んでください．

非常に初歩的な問題から中級クラスの問題まであるのに，「上記の問題の解答を過程も含めて教えてくれないでしょうか？」は無理です．せめて，初歩的な6,7,8は自力で勉強してくれないと，後の解説ができません．

それか，他の問題を捨てて，6,7,8だけに集中するか(ただし，みなさん答えだけを教えるつもりはないと思いますよ)．

どちらかの選択をした方がよいとおもいますが．

mNeji さんのレス (2008/07/12(Sat) 22:55)

ぼやさん，初めまして．

前回の質問から，興味深く拝見しています．というのも，私は，大学ではほとんど授業にでず，独学と，少数の友人達との論議で過ごしました．ところが，専門外の単位では仕方なく出席することが多かったです．其のおかげで，音楽の講義でショパン論を詳しく聴いて，その作品も好きになったり，地震の講義で「予測出来た時にどのように市民に伝達するべきか？」といった熱いバトルをお聞きしたりと，意外と印象に残っていたりします．

私のときは，音楽で言えば「J.S.Bach論」を好きに書き，地震で言えば「確率予測では行政側の経済的補償のリスクが多すぎる論」を書かせて頂きました．すなわち，調べなくても良いようにしました．

逆に，ばやさんが意外と回答を真っ向から書こうとされている点が理解出来ないでいます．多くの方がご指摘のように，問題レベルは高校生〜大学生とバラバラです．いったい，どのような分野の大学で，どのような科目として講義されているのか，そもそも，一つの講義の問題なのかとか，とても理解出来ずにいます．

普通，他学科選択としての物理の講義なら「それなりに整理された問題」をだすように思えますね．ここら辺も含めて，解説ねがえれば幸いです．

ぼや さんのレス (2008/07/12(Sat) 23:17)

はい，私は放射線技術学科に所属しています． 物理学自体は高校のときに習っていなかった人たちに合わせたり，後少々先生が変人なのもあるので，問題のレベルがバラバラな時が結構あるのです． あ，それとこれは一つの講義で出されたものいです．

mNeji さんのレス (2008/07/13(Sun) 00:52)

とすると他学科選択というよりは必須科目ななのでしょうかね．本当に教え方が納得出来ないならば，学生同士話し合った上で，理解出来ない点を申し出た方がいいように思います．

一部，説明してみます．高校の微分積分の範囲のような気もしますが...．

＞問題1：平均の速さと瞬間的な速さの違いを，おのおの定義式を用いて，さらにそれぞれの幾何学的意味を説明せよ．

t=0の時に座標原点にいた物体が，時間に伴って進んだ距離をx(t)とする．

その物体がある時刻tにいる時の瞬間的な速度v(t)は，

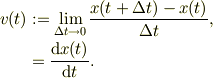
＃数学で，縦軸をx(t),横軸をtとして図示した時に，tの近くで接線を書いた時の傾きに相当します．

その物体が，t=0から時刻tまでに進む平均速度<v(t)>は，

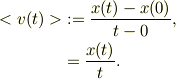
＃数学で，縦軸をx(t),横軸をtとして図示した時に，0〜tの間に進んだ距離x(t)を平均的に進んだとした速度になります．

これで，問い1,2,4は解けませんか？その応用問題として問い3,5は解けるように思います．自分でやって途中で止まった所まで書いて見て下さい．

mNeji さんのレス (2008/07/13(Sun) 11:20)

近くのスレッドの関連で調べた次のサイト，

力学のページ

• http://www14.plala.or.jp/phys/mechanics/index.html

は，ご質問の問いにかなり密接なご解説をされているように思います．一読をお勧めします．

ぼや さんのレス (2008/07/13(Sun) 16:54)

問題4は， Δｘ＝ｘ（ｔ１）−ｘ（ｔ０） Δｔ＝ｔ１−ｔ０ と出たんですが，こっからどうすればいいんでしょうか？ 速度vはどう計算すれば良いんでしょうか 問題3の(b)は15(m)でいいんでしょうか？

mNeji さんのレス (2008/07/13(Sun) 20:37)

先ほどプールから帰って空腹時に返答を書いたのですが，機嫌が悪く，キツい事を書いたので修正します．

この問題を見てみると，問題は２つになります．

＞問題4a：等速度vでx軸上を運動する質点が，時刻tにおける座標がx=x0＋vtと表されるとき，これからΔx/Δt=vを導け．

このとき，授業で「Δx/Δt」をどのように説明したのかに依ると思います．

（１）差分で計算する場合 （２）普通の微分で計算する場合

ところが， ＞Δｘ＝ｘ（ｔ１）−ｘ（ｔ０） ＞Δｔ＝ｔ１−ｔ０

とお書きになっているので，手間ですが（１）の方法で考えて見ます．

Δｘ＝ｘ（ｔ１）−ｘ（ｔ０） ＝{x0＋v*t1}-{x0＋v*t0} ＝v(t1-t0} ＝vΔｔ

よって， Δｘ／Δｔ＝v

＞問題4bまた，xがtの関数として ＞x=1/2αt^2＋v0t＋x0 ＞で与えられるとき(α,v0,x0は定数)，速度vを計算せよ．

同様に計算しますが，時間をt0→t，t1→t+Δｔ，とします．

Δｘ＝ｘ（ｔ１）−ｘ（ｔ０） ＝ｘ（t+Δｔ）−ｘ（t） ＝{1/2α(t+Δｔ)^2＋v0(tΔｔ)＋x0}-{1/2α(t)^2＋v0(t)＋x0} ＝{1/2α(t^2+2tΔｔ+Δｔ^2)＋v0(t+Δｔ)＋x0}-{1/2α(t)^2＋v0(t)＋x0} ＝{1/2α(2tΔｔ+Δｔ^2)+v0Δｔ} ＝{αt+1/2αΔｔ+v0}Δｔ よって， 速度V(t)＝Δｘ／Δt ＝{αt+1/2αΔｔ+v0}←Δｔの項は，微少量なので無視出来て 〜αt+v0

同様に加速度A(t)は， A(t) =ΔV/Δｔ

ΔV=V(t+Δｔ)-V(t) で定義されます．先に求めたV(t)を用いて，ご自分で解いて下さい．

＞問題3の(b)は15(m)でいいんでしょうか？

式を立てて説明して下さい．

もし，授業で使われている教科書が，近くの図書館等で私にも見える様でしたら教えて下さい．

mNeji さんのレス (2008/07/14(Mon) 09:00)

昨日，問題4の回答を書いた後で気づいた事があります；この問題集は，教官の方が，授業中の説明を補佐する為に，わざわざ製作されて次の授業までの宿題にされていられるのではないでしょうか．

放射線技術学科といえば，X線像の撮影，CTとかMRIの測定と画像解析などをされる訳ですね．これらの装置の動作原理を知ることが大切でしょうね．また，自分が骨折で入院した経験でいえば，怪我をした人の測定では，安全であることはもちろん，痛みの少ないような配慮も大切です．それには，人体の力学的理解も望まれましょう．

その意味でも，基礎的な物理，数学を身につけて貰いたい，というのが教官の方の願いだろうと思います．しかし，ご質問を拝見していると，先ずは，高校の数学と物理の教科書をもう一度見直すべきだと思います；

●数学 微分 ベクトル ●物理 運動

ついては，その教官の方に，どのような点を注意して勉強すればいいか，ご質問されたら良いとおもいますが，如何でしょうか．

toorisugari no Hiro さんのレス (2008/07/14(Mon) 12:56)

mNejiさんもおっしゃっていますが，おなじ事を繰り返します．

ぼやさんは以前「物理はいらない」とおっしゃってましたが，それは間違いです．

医療関係者なら「物理を知らないとプロにはなれない」．これは介護やリハビリをやっている友人の言葉です．まして，放射線技師なら電磁気，原子・分子，放射線，等の高度な知識を必要とする講義が待ち受けています．必要ないわけありません．

もちろん，物理学科相当の知識や能力までは必要でなく，理工系大学に入学できる程度の力があればいいので，余り声を大にして言われないのでしょう．それで，新入生のぼやさんは勘違いされていると思います．でも，今のぼやさんの力では専門の講義についていけないのではないかと危惧します．

最低でも，高校の物理・数学の初歩はマスターしておかないと厳しいと思いますが，それが，この課題のレベルです．