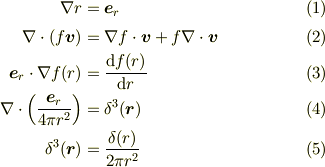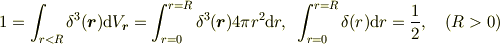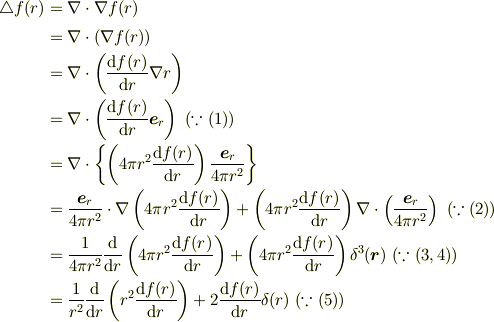無限空間でのヘルムホルツ方程式のグリーン関数

無限空間でのヘルムホルツ方程式のグリーン関数

チャパ さんの書込 (2007/10/05(Fri) 11:15)

極座標で表したラプラシアンをつかってヘルムホルツ方程式のグリーン関数の両辺を体積積分すると，右辺のδ関数のほうは解が−1になるのにたいし，反対の左辺は僕が計算すると0になってしまします(汗)，何でこんなことになるのでしょうか？

携帯なのであまり数式は打てませんが

｛(1/ｒ^２)・ｄ／ｄｒ(ｒ^２・ｄ／ｄｒ)＋ｋ^２｝・ｅ^(ｉｋｒ)／４πｒ ＝−δ(Ｘ−Ｙ)

なんです．これを座標Ｙを中心とする半径εの球領域を体積素ｄτ＝４πｒ^２ｄｒで積分するんです．

ｅはネイピア数 ｉは虚数単位 ｒ＝｜Ｘ−Ｙ｜ ｋも変数です．

どうしても分からないのでお願いします．

Re: 無限空間でのヘルムホルツ方程式のグリーン関数

チャパ さんのレス (2007/10/05(Fri) 11:28)

この本ではこの後 ｒｅ^(ｉｋｒ)＝−ｉ(ｄ／ｄｋ)ｅ^(ｉｋｒ) という関係式を使っています．

Re: 無限空間でのヘルムホルツ方程式のグリーン関数

チャパ さんのレス (2007/10/05(Fri) 15:25)

HIROさんありがとうございます[if9cf]今からバイトなんで，バイトおわってからネットカフェでみてみます[if9cf]ありがとうございます[if9cf]

Re: 無限空間でのヘルムホルツ方程式のグリーン関数

toorisugari no Hiro さんのレス (2007/10/06(Sat) 00:50)

この手の計算をするときには電磁気学でおなじみの

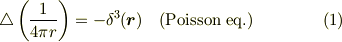
\triangle \left( \frac{1}{4\pi r}\right) &= - \delta^3(\bm{r}) \quad\text{(Poisson eq.)}\tag{1}

もしくは

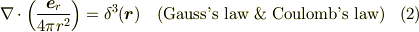
\nabla \cdot \left( \frac{\bm{e}_r}{4\pi r^2}\right) &= \delta^3(\bm{r})\quad\text{(Gauss's law \& Coulomb's law)}\tag{2}

(ただし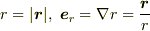， r=|\bm{r}|,~\bm{e}_r = \nabla r = \frac{\bm{r}}{r} です．)をa prioriな公式として使った方が便利です．(「導出」したい場合は先の過去log参照)

あるいは今回のように原点に特異性を持つ関数の r 積分を行うのなら

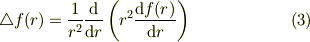
\triangle f(r) &= \frac{1}{r^2} \frac{\mathrm{d}}{\mathrm{d}r}\left(r^2 \frac{\mathrm{d}f(r)}{\mathrm{d}r} \right) \tag{3}

でなく，付加項をつけた

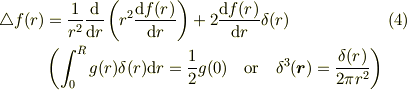
\triangle f(r) &= \frac{1}{r^2} \frac{\mathrm{d}}{\mathrm{d}r}\left(r^2 \frac{\mathrm{d}f(r)}{\mathrm{d}r} \right) + 2 \frac{\mathrm{d}f(r)}{\mathrm{d}r}\delta(r)\tag{4} \\&\left(\int_0^R g(r)\delta(r)\mathrm{d}r = \frac{1}{2}g(0)\quad \text{or} \quad \delta^3(\bm{r})= \frac{\delta(r)}{2\pi r^2}\right)

で計算した方がよいでしょう．(原点で微分可能な関数なら付加項は利きません．)

# (4)式は(2)式と 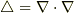\triangle = \nabla\cdot\nabla から導かれます．

Re: 無限空間でのヘルムホルツ方程式のグリーン関数

チャパ さんのレス (2007/10/06(Sat) 11:05)

ヒロさん本当にありがとうございます．

昨日はネットカフェにいけなかったのですが今日いって3時間くらいかけてみてみます． (携帯なので文字化けしちゃうので見れないんですスミマセン，汗)

Re: 無限空間でのヘルムホルツ方程式のグリーン関数

チャパ さんのレス (2007/10/07(Sun) 15:32)

すみません通りすがりのヒロさん． 追加項を付けても矛盾しないことや，積分で『−1』になることも確かめられましたが，(2)から(4)が導けません(汗)

なにかヒントくださいませんか．答えでもいいですが(笑)

Re: 無限空間でのヘルムホルツ方程式のグリーン関数

toorisugari no Hiro さんのレス (2007/10/09(Tue) 11:07)

\nabla r &= \bm{e}_r \tag{1}\\\nabla\cdot(f\bm{v})&=\nabla f \cdot \bm{v} + f \nabla\cdot\bm{v} \tag{2}\\\bm{e}_r \cdot \nabla f(r)&= \frac{\mathrm{d}f(r)}{\mathrm{d}r} \tag{3}\\\nabla \cdot \left( \frac{\bm{e}_r}{4\pi r^2}\right) &= \delta^3(\bm{r}) \tag{4}\\\delta^3(\bm{r}) &= \frac{\delta(r)}{2\pi r^2} \tag{5}

を使います．(式(5)は

1 = \int_{r<R} \delta^3(\bm{r}) \mathrm{d}V_{\bm{r}} = \int_{r=0}^{r=R} \delta^3(\bm{r}) 4\pi r^2 \mathrm{d}r ,~\int_{r=0}^{r=R} \delta(r) \mathrm{d}r &= \frac{1}{2},~ &(R > 0)

から出てきます．)

これより，

\triangle f(r) &= \nabla\cdot\nabla f(r)\\&= \nabla\cdot(\nabla f(r))\\&= \nabla\cdot\left(\frac{\mathrm{d}f(r)}{\mathrm{d}r} \nabla r\right)\\&= \nabla\cdot\left(\frac{\mathrm{d}f(r)}{\mathrm{d}r}\bm{e}_r\right) ~(\because (1))\\&= \nabla\cdot\left\{\left(4\pi r^2 \frac{\mathrm{d}f(r)}{\mathrm{d}r}\right) \frac{\bm{e}_r}{4\pi r^2} \right\}\\&= \frac{\bm{e}_r}{4\pi r^2} \cdot \nabla\left(4\pi r^2 \frac{\mathrm{d}f(r)}{\mathrm{d}r}\right) + \left(4\pi r^2 \frac{\mathrm{d}f(r)}{\mathrm{d}r}\right) \nabla\cdot\left(\frac{\bm{e}_r}{4\pi r^2} \right)~(\because (2))\\&= \frac{1}{4\pi r^2}\frac{\mathrm{d}}{\mathrm{d}r}\left(4\pi r^2 \frac{\mathrm{d}f(r)}{\mathrm{d}r}\right) + \left(4\pi r^2 \frac{\mathrm{d}f(r)}{\mathrm{d}r}\right) \delta^3(\bm{r})~(\because (3,4))\\&= \frac{1}{r^2}\frac{\mathrm{d}}{\mathrm{d}r}\left(r^2 \frac{\mathrm{d}f(r)}{\mathrm{d}r}\right) + 2 \frac{\mathrm{d}f(r)}{\mathrm{d}r} \delta(r)~(\because (5))

となります．

Re: 無限空間でのヘルムホルツ方程式のグリーン関数

チャパ さんのレス (2007/10/09(Tue) 11:15)

本当にありがとうございます． 無知な僕のために時間をさいていただき感謝してます．

今からネットカフェにいってみてきます．ありがとうございます．

Re: 無限空間でのヘルムホルツ方程式のグリーン関数

チャパ さんのレス (2007/10/09(Tue) 12:08)

toorisugari no Hiro さんありがとうございます． いま見てみましかが抵抗なく読めました． 疑問が解けてすっきりしました（笑）