電荷密度を積分する場合
電荷密度を積分する場合
けん(大学1年) さんの書込 (2007/01/18(Thu) 16:59)
静電ポテンシャル
φ(r)=(Ae^(-kr))/r
に対し,ポアソンの方程式から,電荷の体積密度が
ρ(r)=-(εA(k^2)e^(-kr))/r
と,分かりました. このとき,
∫(0から無限大まで)(ρ(r)4πr^2)dr
は,原点にある点電荷の電荷は含まないんですか?原点は積分範囲に入っているので,原点の点電荷も含まれると思ったのですが,違うのでしょうか?
Re: 電荷密度を積分する場合
ミュフ猫 さんのレス (2007/01/18(Thu) 19:58)
けんさんへ
>∫(0から無限大まで)(ρ(r)4πr^2)dr > >この積分式においては,原点の点電荷は考慮されていません. >なぜなら,この式の被積分関数がr=0のとき, >ρ(r)4πr^2=-(εA(k^2)e^(-kr))*(4πr)=0 >となってしまっているからです.点電荷は体積が0で,電荷密度が無限大です. >よって,体積積分の時に,その積分範囲に含まれることがわかれば, >その点電荷の位置の被積分関数が0になるように積分式を立てて解き, >重ね合わせの原理を用いて,点電荷の電荷量だけ後から加算すればよい >と思います.
(このレスは,大間違いです.読み飛ばしてください.すみません.)
Re: 電荷密度を積分する場合
けん(大学1年) さんのレス (2007/01/20(Sat) 18:41)
レスありがとうございます.
>点電荷は体積が0で,電荷密度が無限大です.
ρ(r)4πr^2=-(εA(k^2)e^(-kr))*(4πr)=0
0X∞がここでは0だから,原点での点電荷は含まれないということを表しているのですか?
Re: 電荷密度を積分する場合
サボテン さんのレス (2007/01/20(Sat) 19:31)
ミュフ猫さんの仰るとおりです. 但し,点電荷の体積密度はデルタ関数に比例します. ここでは質問文を拝見する限り,連続的に分布している電荷密度を扱っているのではないでしょうか? 点電荷とは異なります.
ですので,私としては「原点にある点電荷」と言うより, 「原点の電荷密度が無限大」と言う表現の方が適切であると思います.
原点の電荷密度は無限大ですが,その発散の程度はO(1/r)であり, 原点を中心とした微小球殻4πΔr^2に含まれる電荷量は0になります. よって積分範囲に含めても良いです.
さらに数学的に厳密には広義積分を用いる必要がありますが,物理では そこまで考える必要はないでしょう.
Re: 電荷密度を積分する場合
けん(大学1年) さんのレス (2007/01/20(Sat) 19:40)
ありがとうございます. 広義積分というのは,ここでは,積分範囲を(εから∞)にして,積分後にε→0とすればいいのでしょうか?
Re: 電荷密度を積分する場合
サボテン さんのレス (2007/01/20(Sat) 19:54)
はい,その通りです.でも物理はそこら辺の扱いが結構いい加減なので, ∫(0〜∞)で良いと思いますよ. 実際,私が電磁気を習った頃はあまり気にせず積分してました(^^) 積分できてしまえば,あとはあまり深く考えてませんでした・・・.
後々,物理では場の量子論を習うようになりますが,くりこみの話 なんて∞に∞を相殺させて有限の値にするとか, 経路積分は無限回積分するとか結構無茶をするものです.
物理にとっては直感力の方が重要だと思いますので,もしけんさんが 物理の方面に進む場合は,そちらを磨いた方が有益だと思います.
以上年寄りの独り言でした.
Re: 電荷密度を積分する場合
なんとなく さんのレス (2007/01/21(Sun) 10:14)
よこから,失礼します.
ミュフ猫さんやサボテンさんの言われる通りなのですが,どこがネックなのか,1回生では少し分かり辛いかも知れません.おそらくポアソンの式, ∇^2φ=-ρ/ε0 から球対称ポテンシャルφを直接微分してρ(r)を求めていることでしょう.しかし,こうして得られる解はr≠0のときの解のみです.r→0のときの解は ∇^2(1/r)=-4πδ(r)に注意すれば,電荷によるポテンシャルはψ=q/4πε0rであるから,結局, ρ(r)=qδ(r)-(ε0A(k^2)e^(-kr))/r となるのではないでしょうか. 「湯川型」ポテンシャルは点電荷(のみ)からは導けないんでしょうね.
Re: 電荷密度を積分する場合
りんご さんのレス (2007/01/21(Sun) 12:06)
けんさん,
難しい積分の話だろうと思って見てなかったのですが,コメントさせてください.
>静電ポテンシャルφ(r)=(Ae^(-kr))/rに対し,ポアソンの方程式から,電荷の体積密度がρ(r)=-(εA(k^2)e^(-kr))/rと,分かりました.
と在りますが,この場合,3次元極座標で考える訳ですよね.すると,球対称の静電ポテンシャル関数に対するポアソンの方程式は,
![\rho(r) &= -\varepsilon \nabla^2 \phi(r) \\&= -\varepsilon [r^{-2}\partial_{r}(r^2\phi(r))]](http://hooktail.maxwell.jp/bbslog/3c35b86a73f9c8edebbd1434ce216dce.png)
だと思います.もしそうなら,上記の式の微分を実行すると違う結果になる様ですが,如何でしょうか?
と書きましたが,自分はチョンボをしてました.訂正します.
![\rho(r) &= -\varepsilon \nabla^2 \phi(r) \\&= -\varepsilon [r^{-2}\partial_{r}(r^2\partial_{r}(\phi(r)))]\\&= -\varepsilon k^2 \frac{\mathrm e^{-kr}}{r}](http://hooktail.maxwell.jp/bbslog/7a95b74fe86c9bfb7bac1b1e0407bab7.png)
上記の最後の符号は間違っていました.(訂正2007-01-25 03:48)
推測ですが,2次元(平面)の極座標を使われていませんでしょうか? ←取り下げ.
すると,逆問題,電場についてのガウスの発散公式での電荷の体積分について論議されているのだと思いますが,上記の電荷分布に点電荷を含むと考える必要はないように思えます.むしろ,単純なクーロン的な力が指数関数的に遮蔽された場合の振る舞いを考察していますが,この場合には,遮蔽の要因と点電荷は不可分と見るべきと思います.これは原理的な要点とおもいます.
他方,球対称関数の体積分の微小体積要素は 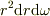 ですから,原点での発散の心配は無いと思います.これは積分の技法の要点ででしょう.その数学的な論議は存じません....
ですから,原点での発散の心配は無いと思います.これは積分の技法の要点ででしょう.その数学的な論議は存じません....
以上,間違った発言をお許しください.
==== オッチョコチョイの素人には,判りやすい公式集が欲しいところです.
Re: 電荷密度を積分する場合
MXK さんのレス (2007/01/23(Tue) 14:15)
原点の点電荷も含めると
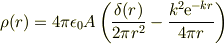
となると思われます. 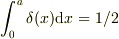
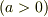 などに注意して積分すると所望の結果が得られると思います.(係数が違っているような気がするので,とりあえず訂正しておきます.)
などに注意して積分すると所望の結果が得られると思います.(係数が違っているような気がするので,とりあえず訂正しておきます.)
Re: 電荷密度を積分する場合
toorisugari no Hiro さんのレス (2007/01/24(Wed) 17:03)
もう問題は解決しているのですが,口出しさせてください.
ご質問の意味がわからなかったのですが,
「
(1) 極座標表示のポアッソン方程式に湯川型静電ポテンシャル 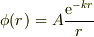 を与えて,電荷分布
を与えて,電荷分布 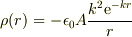 が得られた.
(2) 広義積分
が得られた.
(2) 広義積分 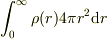 により,総電荷量を計算すると非零の値が得られる.
(3) しかし,(ポテンシャルから導いた電束密度ベクトル
により,総電荷量を計算すると非零の値が得られる.
(3) しかし,(ポテンシャルから導いた電束密度ベクトル 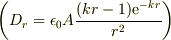 に十分遠方の球面上でガウスの定理(法則)を適用することで得られる,総電荷量は0に収束するので,)(2)は矛盾.
(4) この矛盾は広義積分のやり方に問題があるためなのか?
」
ということですね.
に十分遠方の球面上でガウスの定理(法則)を適用することで得られる,総電荷量は0に収束するので,)(2)は矛盾.
(4) この矛盾は広義積分のやり方に問題があるためなのか?
」
ということですね.
なんとなくさん,りんごさん,MXKさんがおしゃっているように,電荷分布の式が間違っている(遮蔽となる電荷分布だけしか得られず,原点にあるはずの点電荷が含まれていない)ためですね.
極座標系のラプラシアンは 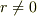 でしか定義されていないので,
原点に
でしか定義されていないので,
原点に  関数型の電荷があっても出てきません.(ですから
関数型の電荷があっても出てきません.(ですから 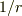 を極座標表示のポアッソン方程式に代入しても
を極座標表示のポアッソン方程式に代入しても 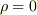 となり点電荷が出てきません.)
となり点電荷が出てきません.)
それを解決するにはいくつか方法があって
(1) なんとなくさんがおしゃるように,
原点に  関数型の点電荷(電荷量未定)を付け加えて,無限遠方における電束密度ベクトルに対するガウスの定理(法則)から電荷量を決定する.
(2) 場が回転対称なら,最初から,半径
関数型の点電荷(電荷量未定)を付け加えて,無限遠方における電束密度ベクトルに対するガウスの定理(法則)から電荷量を決定する.
(2) 場が回転対称なら,最初から,半径  の球殻上でガウスの定理を電束密度ベクトルに適応し,半径
の球殻上でガウスの定理を電束密度ベクトルに適応し,半径  の球に含まれる電荷から,電荷分布を決定する.(「
の球に含まれる電荷から,電荷分布を決定する.(「 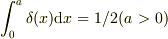 などに注意」)
(3) 原点の特異性を避けるためにポテンシャルの中の
などに注意」)
(3) 原点の特異性を避けるためにポテンシャルの中の 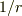 を
を 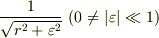 と「粗視化」し,極座標系のラプラシアンに代入し,計算の後極限(
と「粗視化」し,極座標系のラプラシアンに代入し,計算の後極限( 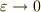 )をとる.ただし,このとき
)をとる.ただし,このとき  関数に(弱)収束する関数
関数に(弱)収束する関数 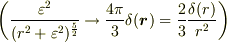 に注意する.(用心しないとナイーヴな極限操作で消してしまう.)
に注意する.(用心しないとナイーヴな極限操作で消してしまう.)
(3)の方法については
「数理科学SGCライブラリ-39 マクスウェル方程式」北野 正雄・著,サイエンス社,2005.
の「デルタ関数と超関数」という章に詳しいです.(  関数の粗視化)
関数の粗視化)
# 計算していないので,わからないのですが,原点に双極子がある場合のポテンシャルを,極座標系のラプラシアンに(何も考えず)代入すると,ちゃんと双極子が現れるのかな?
Re: 電荷密度を積分する場合
MXK さんのレス (2007/01/25(Thu) 00:19)
解決(2)に近いですが, 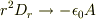
 から原点の電荷を決める手もありますね.
># 計算していないので,わからないのですが,原点に双極子がある場合のポテンシャルを,極座標系のラプラシアンに(何も考えず)代入すると,ちゃんと双極子が現れるのかな?
双極子の場合はゼロになってしまって,そのままでは特異性は検知できないのかも知れません.
(式訂正しました.)
から原点の電荷を決める手もありますね.
># 計算していないので,わからないのですが,原点に双極子がある場合のポテンシャルを,極座標系のラプラシアンに(何も考えず)代入すると,ちゃんと双極子が現れるのかな?
双極子の場合はゼロになってしまって,そのままでは特異性は検知できないのかも知れません.
(式訂正しました.)
Re: 電荷密度を積分する場合
toorisugari no Hiro さんのレス (2007/01/25(Thu) 01:12)
> 解決(2)に近いですが, 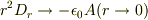 から原点の電荷を決める手もありますね.
から原点の電荷を決める手もありますね.
なるほど,特異性(クローン電場成分)だけをとりだすのですね. 方法(4)としましょう.
>> # 計算していないので,わからないのですが,原点に双極子がある場合のポテンシャルを,極座標系のラプラシアンに(何も考えず)代入すると,ちゃんと双極子が現れるのかな? > 双極子の場合はゼロになってしまって,そのままでは特異性は検知できないのかも知れません.
まだ,自分で計算してないですが...
もしそうなら,回転対称でないポテンシャルの場合は(1)の方法において  関数だけでなく,その微分(多重極子)も加えないとダメと言うことですか...無限個(双極子,4重極子,...)のパラメータが出てきて解けそうにないですね.
(2)の方法(ガウスの法則)だと双極子は検知できません.ダメ.
関数だけでなく,その微分(多重極子)も加えないとダメと言うことですか...無限個(双極子,4重極子,...)のパラメータが出てきて解けそうにないですね.
(2)の方法(ガウスの法則)だと双極子は検知できません.ダメ.
(3)の方法及び(4)の方法がこの場合も有効かな? ((3)の方法は粗視化の方法を変えないと高次の多重極子は検知しないとすでに紹介した文献にありました.)
Re: 電荷密度を積分する場合
りんご さんのレス (2007/01/25(Thu) 04:20)
このところ,流体力学の計算と入り交じって,計算ミスを多発しているのでコメントを控えていました.
話を単純にできないかと思い,半径rの球面に含まれる電荷量Q(r)を出してみる事にしました.
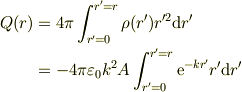
積分で部分積分をすると(あまり自信は無いのでチェック願いたいですが),
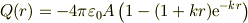
となっています.まさか定数項が出てくるとは思わなかったので驚いています.
面白い事に, 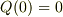 で,
で, 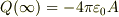 となりますね.まるで;
・原点近傍では電荷がなく(遮蔽)され,
・遠方では,逆に,有限電荷を持つ,
ように見えるかのようです.
となりますね.まるで;
・原点近傍では電荷がなく(遮蔽)され,
・遠方では,逆に,有限電荷を持つ,
ように見えるかのようです.
問題は静電ポテンシャルの勾配と矛盾する事ですね.形式的には原点に 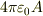 の点電荷を持ってくれくれば,電場は思い通りになりますが....やはり点電荷のばあいの特殊事情を考慮することが出来るようにも思えます.
の点電荷を持ってくれくれば,電場は思い通りになりますが....やはり点電荷のばあいの特殊事情を考慮することが出来るようにも思えます.
けんさんの質問に戻ってしまったように思いますが,これはいったいどういうことか,いまだ解釈できません.
Re: 電荷密度を積分する場合
ミュフ猫 さんのレス (2007/01/25(Thu) 08:36)
りんごさんへ
>問題は静電ポテンシャルの勾配と矛盾する事ですね.
リンゴさんが求められた半径rの球面に含まれる電荷量Q(r)は,原点の点電荷を 無視した電荷密度分布を用いて計算されているのだと思います. つまり,原点の点電荷は正電荷,原点以外の場所の電荷密度分布は負電荷 ということだと思います. ちなみに点電荷が存在するときは, 1,その点での静電ポテンシャルが無限大に発散する. 2,その点への電場の大きさの極限値が無限大に発散する. 3,その点での電荷密度が無限大に発散する. と言えると思います. ところが,点電荷が存在しないときは, 1,その点での静電ポテンシャルがある有限値を取る. 2,その点への電場の大きさの極限値が有限値を取る. (近づける方向によって,その有限値が異なる可能性がある.) 3,その点での電荷密度は「有限値または,無限大」となる. と言えると思います. つまり,電荷密度が無限大に発散しても,点電荷が存在するとは限りません. また,電荷密度が無限大に発散し,かつ点電荷が存在しないときは, 1,その点での静電ポテンシャルの空間微分(勾配の定義)が不可能である. 2,その点への電場の大きさの極限値が有限値を取る. (近づける方向によって,その有限値が異なる可能性がある.) と言えて,電荷密度が有限値を取るときは, 1,その点での静電ポテンシャルの空間微分(勾配の定義)が可能である. 2,その点での電場があるベクトル値を取る. と言えると思います.
Re: 電荷密度を積分する場合
りんご さんのレス (2007/01/25(Thu) 11:02)
ミュフ猫さん,はじめまして.
正に,私の判らない点をお書きくださいました:
ーーーー引用はじめ 半径rの球面に含まれる電荷量Q(r)は,原点の点電荷を 無視した電荷密度分布を用いて計算されているのだと思います. つまり,原点の点電荷は正電荷,原点以外の場所の電荷密度分布は負電荷 ということだと思います. ーーーー引用終わり
他方,私は,この問題は全て,けんさんの冒頭の発言に於いてあるように;
ーーーー引用はじめ 静電ポテンシャルφ(r)=(Ae^(-kr))/rに対し,ポアソンの方程式から, 電荷の体積密度がρ(r)=-(εA(k^2)e^(-kr))/rと,分かりました. ーーーー引用終わり
だけであると考えます.
この問題では,静電ポテンシャルが与えられているだけで,点電荷の存在が先験的に与えられているとは思えません.問題のなかに,他の荷電体の存在が入っていれば,それはそれで別の問題だと感じますが.
私は,数学的な厳密な定義や考え方を知りませんが,上記のご解説の見地からすると,静電ポテンシャルφ(r)=(Ae^(-kr))/rが与えられると,自然な計算の元に,「点電荷を含んだ電荷Q(r)」を求める事ができるのかを,お教えいただけますか?
Re: 電荷密度を積分する場合
ミュフ猫 さんのレス (2007/01/25(Thu) 12:08)
りんごさんへ
やり方はいろいろあると思います. まず,原点の点電荷量の一般的な導出方法は, ガウスの法則を利用します. Q(r) = ε*∫(-gradφ(r)・n↑)dS より, Q(0) =lim[r→0]{ε*∫(-gradφ(r)・n↑)dS} となり,原点の点電荷量Q(0)が得られます.
もう1つは,ポアソンの方程式より,原点以外の電荷密度分布ρ(r)を求め, それを体積積分し,原点を中心とした半径rの球面内で,原点を除いた領域 に内在する電荷量Q'(r)を求めます. Q'(r) =∫[r'=0〜r]ρ(r')dv そして,ガウスの法則で求めたQ(r)から,Q'(r)を差し引いて, Q(0) =Q(r)-Q'(r) となり,原点の点電荷量Q(0)が得られます. つまり,Q'(r)の定数項が原点の点電荷量ということですね.w
Re: 電荷密度を積分する場合
yama さんのレス (2007/01/25(Thu) 13:32)
>静電ポテンシャル φ(r)=(Ae^(-kr))/r に対し,ポアソンの方程式から,電荷の体積密度が ρ(r)=-(εA(k^2)e^(-kr))/r と,分かりました.
これは正確ではないと思います.正確には
静電ポテンシャル φ(r)=(Ae^(-kr))/r に対し,ポアソンの方程式から,r≠0 のところの電荷の体積密度が ρ(r)=-(εA(k^2)e^(-kr))/r と,分かりました.
とすべきだと思います. r≠0 の電荷密度の式をどのようににひねくりまわしても,r=0 の点電荷は出てきません.たとえば r→0 の極限をとっても r=0 の電荷密度にはなりません. r=0 の電荷を導き出すには,r=0 を含む領域にも適用できるような方法が必要になります. 具体的には,既に多くの方々が書かれているように,ガウスの法則とか,δ関数を含む公式などを用いる方法です.
同様のことは,ポテンシャル φ=k/r のときの電荷分布を求める場合にも起こります. ポアソンの方程式から r≠0 の電荷密度が ρ(r)=0 になることが分かりますが,ρ(r)=0 をどうひねくりまわしても原点の電荷は出てきません.
Re: 電荷密度を積分する場合
りんご さんのレス (2007/01/25(Thu) 14:00)
みなさんのご論議から,数式のハンドリングの問題というより,この問題には,なんらかの物理的境界条件,例えば,「遠方で電場がゼロになる」といった物理的な要請が欠けているように思います.この立場で,検討をしてみます.
Re: 電荷密度を積分する場合
yama さんのレス (2007/01/25(Thu) 16:57)
微分方程式から電荷分布を求めるのだったら境界条件が必要だと思いますが,与えられたポテンシャルから電荷分布を求める場合は境界条件は必要ないように思います.
Re: 電荷密度を積分する場合
toorisugari no Hiro さんのレス (2007/01/25(Thu) 18:37)
(追記:以下の 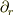 はすべて
はすべて 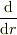 に読み替えてください.ああ,初歩的ミス..)
に読み替えてください.ああ,初歩的ミス..)
静電ポテンシャル 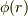 が与えられると,
が与えられると,
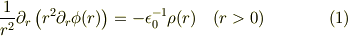
の式から電荷密度 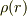 が計算できますが,ここで得られる関数は
が計算できますが,ここで得られる関数は 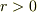 でしか有効でありません.
でしか有効でありません.
たとえば

という静電ポテンシャルから電荷密度を計算すると 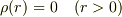 になります.これには原点に点電荷
になります.これには原点に点電荷 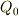 があることは考慮されていませんが,間違いではありません.
があることは考慮されていませんが,間違いではありません.
> 自然な計算の元に,「点電荷を含んだ電荷Q(r)」を求める事ができるのかを,お教えいただけますか?
いろいろ方法がありますが,汎用的な鉄則として 「困ったときは密度量でなく積分したスカラー量で考える.」 が有効だと思います.
密度量には電荷密度,質量密度だけでなく,δ関数,rot,grad,div等も含まれています.これらの量は積分を通して定義されているはずで,この積分式に対して,様々な計算,スケール変換,座標変換を行う方が,密度量に対して同様な事を行うよりわかりやすいし,困難が出にくいです.
では具体的にどうするのかというと原点近傍の電荷分布に関しては,(1)よりも,回転対称な場合のガウスの法則
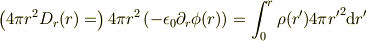
で考える方がよいということです.右辺は半径  の球の「電荷」をあらわしています.この式を微分すると(1)式になるのはすぐわかると思います.
の球の「電荷」をあらわしています.この式を微分すると(1)式になるのはすぐわかると思います.
この式の左辺に(2)式を代入すると
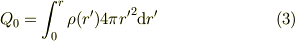
となります.この式の左辺は  によらず一定ですから,原点に電荷
によらず一定ですから,原点に電荷 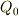 があること(そして
があること(そして 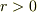 では
では 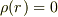 であること)が導けます.
であること)が導けます.
なお,答えを,今のように,電荷と電荷密度の折衷でなく,電荷密度だけで表現したいのなら,(3)式からδ関数を使って 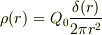 と表すしかないですね.
と表すしかないですね.
Re: 電荷密度を積分する場合
りんご さんのレス (2007/01/25(Thu) 19:44)
toorisugari no Hiroさん,
いささか意見が分かれるようなのですが,今週はあまり時間がないので,簡単にコメントします.
極座標で「r>0」を強く書かれていらっしゃいますが,この由来はなにですか?もし原点における点電荷の為に,形式的に入れるとするならば,それなりに理解できますが,原理的には「r=0」を排除する理由はないと思います.
他方,点電荷を表すのに,デルタ関数を使うのは,表記をシンプルにする為の便法であると,私は考えています.事実,ハドロンも有限体積をもちますし,レプトンである電子だって,荷電もスピンも持ちますから,私としては必ず有限体積をもつと信じています(希望:笑).
従って,私は点電荷のデルタ関数を見ると,有限な微小体積に「+/-e」の電荷が分布すると思ってきました.その方が相対論的なイメージにもあうし,「ひも・膜」などのイメージにも近いと思います.以上は「ヨタ話」ですが.
他の話は,自分でも整理してから,再度質問いたします.ただ,多重極展開の話だけは,強く反対いたします,キッパリ.
Re: 電荷密度を積分する場合
toorisugari no Hiro さんのレス (2007/01/25(Thu) 20:04)
何故に不機嫌になられたのか,わかりかねますが...
> 原理的には「r=0」を排除する理由はないと思います.
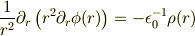
は 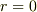 で意味を持っていますか?左辺の最初を見てください.
それだけのことです.
で意味を持っていますか?左辺の最初を見てください.
それだけのことです.
Re: 電荷密度を積分する場合
MXK さんのレス (2007/01/25(Thu) 20:06)
符号やら係数やらを間違えていたので, 訂正をかねてまとめておきます. (数式処理ソフトが出動したので, 今度は大丈夫だと思うのですが...)
式を簡単にするため 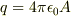 とおく.
与えられたポテンシャル:
とおく.
与えられたポテンシャル:
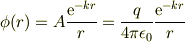
電束密度:
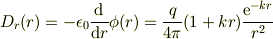
電荷密度(原点以外):
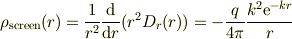
とくに, 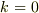 の場合は
の場合は 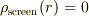 .
.
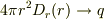
 なので, ガウスの法則から, 原点に電荷
なので, ガウスの法則から, 原点に電荷  があるにちがいない:
があるにちがいない:
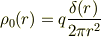
全体の電荷密度:
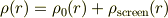
半径  の球内の電荷:
の球内の電荷:
![Q(r)=\int_0^r 4\pi r'^2 \rho(r'){\rm d}r'=qH(r) - q[1-(1+kr){\rm e}^{-kr}]](http://hooktail.maxwell.jp/bbslog/2e4b8c17b5ed86c257f56b00ba42ae08.png)
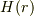 は階段関数で
は階段関数で 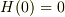 ,
, 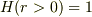 .
. 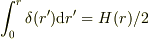 であることに注意.
であることに注意.
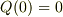 ,
, 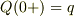 ,
, 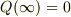 が成り立つ.
が成り立つ.
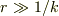 なら, 事実上
なら, 事実上 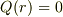 と思ってよい.
と思ってよい.
Re: 電荷密度を積分する場合
りんご さんのレス (2007/01/25(Thu) 20:20)
toorisugari no Hiroさん,
>何故に不機嫌になられたのか,わかりかねますが...
他意はありません.急用ができて,式を書いている時間がないので,気になるところを書いたまでです.つい,気楽に書いてしまい,ご免なさい.論議だけは,チラチラと拝見していますよ.
Re: 電荷密度を積分する場合
りんご さんのレス (2007/01/25(Thu) 22:55)
toorisugari no Hiroさん,
>r=0で意味を持っていますか?左辺の最初を見てください. >それだけのことです.
判りました.深い意味が在るように感じました.というのは,例えば,点電荷の電場で,わざわざ「r>0」と注記しないと思うからです.
残りも,MXKさんの式を見てて理解しました.自分の計算したQ(r)が遮蔽電荷の積分を与えていたのが判り,納得です.
ただし,皆さんはポテンシャルの勾配から,電束密度を出し,その原点近傍のふるまいから点電荷を定めたと思いますが,私は,素直に電場をだして計算しました(笑).
#演習嫌いのツケを漸く払い終えた感じです. #お若い皆さんは,このような馬鹿にならないようにしてくださいね.
私の質問は完了しました.皆さんの,ご説明に感謝します.
Re: 電荷密度を積分する場合
MXK さんのレス (2007/01/25(Thu) 23:57)
toorisugari no Hiro さん
計算していないので,分かりませんが,この問題の場合, ポテンシャルを
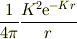
で粗視化してから,微分するといいかも知れませんね.うまく行けば格好いいです.
もちろん,最後に 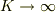 とします.
とします.
Re: 電荷密度を積分する場合
toorisugari no Hiro さんのレス (2007/01/26(Fri) 00:02)
MXKさん 力作ありがとうございます.
一つ重箱の隅をつついていいですか?
> 原点に点電荷  がある
は?です.
がある
は?です.
「原点に電荷  の点電荷 q がある」
「原点に電荷
の点電荷 q がある」
「原点に電荷  がある」
のどちらかにすべきでは?
(私の記事では...見ないことにしてください.)
がある」
のどちらかにすべきでは?
(私の記事では...見ないことにしてください.)
Re: 電荷密度を積分する場合
toorisugari no Hiro さんのレス (2007/01/26(Fri) 00:17)
> 計算していないので,分かりませんが,この問題の場合, ポテンシャルを
> 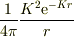 > で粗視化してから,微分するといいかも知れませんね.うまく行けば格好いいです.
> もちろん,最後に
> で粗視化してから,微分するといいかも知れませんね.うまく行けば格好いいです.
> もちろん,最後に 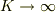 とします.
とします.
えっと,いまざっと計算したところでは
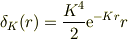
のようですね. 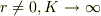 で0,
で0, 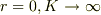 で0.....
で0.....  がじゃまだー.
がじゃまだー.
あと, 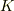 の指数は4でなく2となるべきですね.
の指数は4でなく2となるべきですね.
(追記)
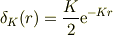
として,逆にポテンシャルを導こうとしましたが, 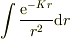 が計算できないので沈没....
が計算できないので沈没....
Re: 電荷密度を積分する場合
MXK さんのレス (2007/01/26(Fri) 00:47)
toorisugari no Hiro さん
点電荷  は修正しました.
は修正しました.
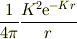
と
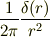
を比較すると,1次元のデルタ関数としては
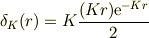
3次元的には
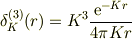
でしょうか.
いずれにせよ,たたみこみは3次元で実施するので,多分結構面倒です.
Re: 電荷密度を積分する場合
りんご さんのレス (2007/01/26(Fri) 12:14)
【この問題を間違った心理状況の説明】ーーー特に回答者の皆様へーーー
回答を正しく受け止められなかった私として,どのような順番で間違いを起こしていったかを順に検討してみました.
[a] 遮蔽電場の静電ポテンシャルの式?
何度も引用して恐縮ですが,けんさんの冒頭の質問で; ーーーー引用はじめ 静電ポテンシャルφ(r)=(Ae^(-kr))/rに対し,ポアソンの方程式から, 電荷の体積密度がρ(r)=-(εA(k^2)e^(-kr))/rと,分かりました. ーーーー引用終わり
を拝見した時点で,上記の式の中に点電荷の成分は無いはずだと思い込みました.
従って,上の電荷密度の体積分をしても点電荷の項が出てこない,言い換えれば,遮蔽成分の電荷密度しかでない,と思っていました.だから,いくら積分を注意しても,点電荷項はでないのだから,問題のなかで; ・点電荷を与える ・遠方境界を与える 必要があると,強く思い込みました.
[b] 極座標を円筒座標でミス計算
No.13843で,[a]の観点から意見をだそうとしましたが,最近計算している,流体の円筒座標での微分と混同して,話が滅茶苦茶になりました.再度,お詫びします.
[c] 遮蔽成分の電荷密度
上の反省で,「遮蔽成分の電荷密度」を出すとなにか判るかなとおもい,半径rにふくまれる「ρ(r)=-(εA(k^2)e^(-kr))/r」の体積分,Q(r)を計算してみました.
計算の前の予想では,Q(r)∝e^(-kr)と思っていました.そして電荷のガウスの発散法則の積分表現から,遮蔽成分の電場が計算されると考えていたのですが,定数項が存在することでした.
慌てて,静電ポテンシャルの勾配から電場を求めてみると,そんな定数項はそんざいしません.
従って,上記の食い違いを検討すれば,点電荷の疑問が判るのだろうと思いました.
#丁度,中心の種の部分がくり抜かれたリンゴをイメージしていたのに, #思いがけないところに種が出てきて驚いた,といった感じでした.
[d] toorisugari no Hiroさんの 解説,No.13879
そのさなか,数学的な観点からのご解説がありました.いくつも判らないところや,計算のあわないところがあったの,直接にご質問したかったのですが,時間がなく,[c]で得た自己矛盾を No.13882に書きました.
自分の感触では,数学的な問題よりは,数式をどう考えるかが重要とおもったので,デルタ関数とか多重極展開の論議はすこし,別問題と思ったからです.
[e] MXKさんの解説,No.13882
目から鱗が落ちました.
自分は,No.13882に書いたように,半径rの内部にある電荷遮蔽電電荷;
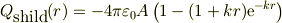
にガウスの法則の積分形を適用すると,異様な遮蔽電場;
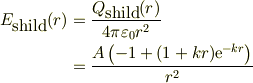
が得られてしまう.
他方,ポテンシャルの勾配から直接電場を計算すると,如何にも遮蔽電場らしい,
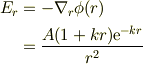
が得られる事です.思い込みが激しかったので,この式に原点での電荷が作る成分があると考えられませんでした. 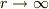 は検討しても,
は検討しても, 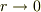 を考えませんでした.それこそ,発散を無意識で嫌ったのかもしれません.
を考えませんでした.それこそ,発散を無意識で嫌ったのかもしれません.
その意味では,原点に近づくと,遮蔽が減少して「原点周辺にある微小体積にある電荷」によるクーロン電場が姿を現していることを理解できました.
なんと言う遠回りをした事か.漸く,皆さんがご指摘になられた解説を,自分の頭でも理解できるようになったと思います.
以上,とても素晴らしい体験をする事が出来たと思います.最初のほうに なんとなくさんの書かれた; >『「湯川型」ポテンシャルは点電荷(のみ)からは導けないんでしょうね.』 は,含蓄のあるように感じます.この歳で判っても,恥ずかしい限りですが,知らないより,断然いいと思いました.
追伸
自分が読んだ本もデルタ関数主体でした.しかしほとんどがデカルト座標でしか使っていなかったと推定します(手元にその本が無いからですが).今回,極座標でのデルタ関数が頻繁に論議されていますが,最近の大学初年度の電磁気学では,そんなにデルタ関数が使われているのでしょうか?
私は,学生の頃は一時,デルタ関数は点電荷を表現するのに,コンパクトで間違えがないと思っていました.でも,そのうちに,点電荷や質点は,計算上の利便性だけで,本来は「微小な体積に詰まっている電荷や質量の分布」と考える方が素直に感じるようになりました.
どうやら,toorisugari no Hiroさんの仰る「粗視化」が,上記のイメージに対応するようですが,それを大学1年生の電磁気に適用できるものなのでしょうか?
そういう意味では,「電場のr依存性の原点周辺の振る舞いを考察する」ような考え方の工夫も大切だと感じました.
また,今回感じたのは,言葉による説明は「あるレベルを超えると,とても有用」だと思いますが,初心者さん達や今回の私のようにご認識をしている者には,数式が添付されるとイメージがとりやすい事を実感しました.
Re: 電荷密度を積分する場合
りんご さんのレス (2007/01/26(Fri) 14:19)
ひょっとして,
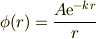
に対して,krを小さくして行きますと原点近傍にある電荷からのクーロン場が出てきますが,これからその電荷を見積もっても良いのではなかろうかと思い至りましたが,どうでしょうか? 丁寧に書けば;
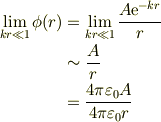
だから,原点近傍にある点電荷ライクな『微小領域に適当に球対称分布する電荷」を考えれば,その微小な半径 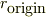 の外では;
の外では;
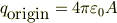
と考える事ができる.
従って,半径rのなかに存在する全電荷は,上記の電荷と遮蔽電荷の重畳で与えられるから;
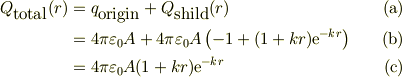
ここで, 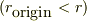 .
.
と考えていいのならば,計算が単純なので理解しやすく,計算違いも少ないでしょうし....
こういう事をいうと,ディラックさんやヘビサイトさんらが天国でクシャミをされているかもしれませんね.
追記
上記の式(a),(b),(c)の流れを見ると,ちょっと常識と違う事に驚かされます.式(a)はいかにもそんな感じですが,式(b)では,原点近傍の電荷を,遮蔽電場を構成する電荷分布の中で,直接的にキャンセルして,再度,指数部がついた項が発生する事です.
従って,両者を合わせた式(c)では原点近傍の電荷はなくなっていて如何にも遮蔽電場の電荷とおもえる「優雅な関数形」を示すように見えます.ところが,なんといっても,その内訳は式(b)の示すような正負点電荷による相互キャンセルといったメカニズムが働いていることですね.
時間が取れたら,中間子の理論を一度眺めさせて戴きたくなりました.
Re: 電荷密度を積分する場合
ミュフ猫 さんのレス (2007/01/26(Fri) 15:21)
りんごさんへ
>従って,半径rのなかに存在する全電荷は,上記の電荷と遮蔽電荷の重畳で >与えられるから; > (与式) >と考えていいのならば,計算が単純なので理解しやすく,計算違いも少ない >でしょうし....
それでいいと思います.つーか,私のレス読んでくれてますか?w そっくりそのまま,記述していますが?w
Re: 電荷密度を積分する場合
りんご さんのレス (2007/01/26(Fri) 15:59)
ミュフ猫さん,
おさっしのように,「重畳」という言葉は,ミュフ猫さんが類似のコメントをされたのを意識して使いました.
私は,「点電荷による電場成分が静電ポテンシャルに含まれないという観点」をとったので,ある半径内での(遮蔽電場の)電荷分布を計算しました.それをどのように考えるかが鍵で,それを模索していただけです.
他方,「点電荷を別途与えるべきだと言う点」については,ミュフ猫さんと同様に,私もそう思いましたが,それを決める論理が判らなかった訳です.遮蔽電場の電荷分布の遠方挙動から推定は付くが,その根拠が付かないし,と思いました.
自分でも,ポテンシャルの勾配から決めた電場と違いからどのように考えるかを模索していた訳です.それで逆質問したところ, No.13885でとても複雑な提案をされたので,自分で計算してから論議の予定でした.
ところが, toorisugari no HiroさんとMXKさんの怒濤の計算論議から,電場ないしはポテンシャルから直接的に点電荷ライクな電荷を推定できるらしいということから見直しをしたレポートとして書いてみました.
自分の誤りは,先に述べたように「点電荷による電場成分が静電ポテンシャルに含まれないという観点」ですが,逆にいえば,遮蔽電場,すなわちポアッソン方程式の解に,点電荷の電場,すなわちラプラース方程式の解が重畳できるのは,ヴェクタ解析の基礎であって,そこまで引用する必要はないと判断しました.もし間違えていたら,ご指摘くださいますか?
やはり数式掲示板での質問では,なかなか思う解が得られなかったり,式の解釈ができなかったりします.できれば式は積極的に開示して,むしろ背景にある物理的な解釈を丁寧にしてくださるとありがたく思います.
Re: 電荷密度を積分する場合
ミュフ猫 さんのレス (2007/01/26(Fri) 16:37)
りんごさんへ
>ところが, toorisugari no HiroさんとMXKさんの怒濤の計算論議から, >電場ないしはポテンシャルから直接的に点電荷ライクな電荷を推定でき >るらしいということから
彼らの導出方法は,ガウスの法則そのものな訳ですよね? 私は,そのことも記述しました.以下の通り.
>ガウスの法則を利用します. >Q(r) = ε*∫(-gradφ(r)・n↑)dS >より, >Q(0) =lim[r→0]{ε*∫(-gradφ(r)・n↑)dS} >となり,原点の点電荷量Q(0)が得られます.
-gradφ(r)は電場です.n↑は面積分における単位法線ベクトルです. つまり,私の書き方が悪すぎたということですね.すみません. 余計に混乱させてしまいました.返信レスありがとうございました.m(_ _)m
Re: 電荷密度を積分する場合
toorisugari no Hiro さんのレス (2007/01/26(Fri) 17:34)
> 私は,学生の頃は一時,デルタ関数は点電荷を表現するのに,コンパクトで間違えがないと思っていました.でも,そのうちに,点電荷や質点は,計算上の利便性だけで,本来は「微小な体積に詰まっている電荷や質量の分布」と考える方が素直に感じるようになりました.
点電荷や質点についてのお考えには疑問がありますが,δ関数については「微小な体積に分布している量」を表すものですから,正しいです.と言うより,δ関数は「一点で無限大ほかは0」という関数ではありません.
# なお,広がりを持つ粒子の理論は湯川さんがすでに考えておられますが,相対論と矛盾するので,うまくいかなかったと聞いています.
> どうやら,toorisugari no Hiroさんの仰る「粗視化」が,上記のイメージに対応するようですが,
「粗視化」のイメージはそのとおりです.δ関数は「一点で無限大ほかは0」という関数ではなく,積分結果が正しい値に十分近いような関数
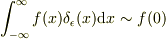 なので,それを明示的に用いているだけです.
なので,それを明示的に用いているだけです.
> それを大学1年生の電磁気に適用できるものなのでしょうか?
そもそも大学1年にラプラシアン,しかも,極座標はないでしょう.だから,ご心配は杞憂です. (追記:と書いてスレ主さんの名前を見たら一年生....こりゃ,問題だしたやつが無茶だ...)
Re: 電荷密度を積分する場合
MXK さんのレス (2007/01/26(Fri) 17:38)
デルタ関数はそもそも変な奴ということで,積分以外の操作が行われるケースは少ないです.特にクーロンの法則を学習中の学生にデルタ関数の極座標表示を持ち出すことは無理でしょう.
しかし,一通り学んだ人や教える立場にある人が全体を整理する段階では,とても有用だと思います.デルタ関数の微分もそうです.この辺りの操作は微妙な部分が多くて,確認のために粗視化の手続きが必要になります.これによってデルタ関数が通常の関数になるので,従来の公式が自由に使えるようになります.(ただし,たたみこみ積分という,不慣れな道具だてが必要で,かなり重くなってしまいます.)
toorisugari no Hiroさんとの怒涛の議論の中心はそこにあるわけで,まだ宿題は残っています(よ).ガウスの定理を陽に使わないで,解析的計算だけで点電荷を出そうというわけです.
(No.13895はとりあえず標準的な答えを確認しておきたかっただけです.)
> (追記:と書いてスレ主さんの名前を見たら一年生....こりゃ,問題だしたやつが無茶だ...)
じゃあ,一年生の解答例を考えましょうか;)
Re: 電荷密度を積分する場合
りんご さんのレス (2007/01/26(Fri) 17:41)
>彼らの導出方法は,ガウスの法則そのものな訳ですよね? >私は,そのことも記述しました.以下の通り.
彼等の論議に付いて,私がコメントするのはおかしいと思うので,もう一度お読みくださいませんか?必ずしもガウスの発散法則の積分形だけで論議していません.
私のろんぎでは,ポテンシャルの勾配から求めた電場,ないしはポテンシャル自身に体する rk<<1の挙動から原点近傍にある電荷の推定をしてみました.そういう意味では,色々な方法が在ります.
またガウスの発散積分をお書きになっていますが,勘が悪くて,理解できませんでした.特に「n↑は面積分における単位法線ベクトル」はあとで質問しようとしました.できれば,この論議は,一番最初の記事に書いていただきたかったです.きっと現役の学生さんなら判るのだろうと思います.
その意味では,ミュフ猫さんの最初のご論議,No.13779で, ーーーー引用開始ーーーーーーーーーーーー ∫(0から無限大まで)(ρ(r)4πr^2)dr
この積分式においては,原点の点電荷は考慮されていません. なぜなら,この式の被積分関数がr=0のとき, ρ(r)4πr^2=-(εA(k^2)e^(-kr))*(4πr)=0 となってしまっているからです.点電荷は体積が0で,電荷密度が無限大です. よって,体積積分の時に,その積分範囲に含まれることがわかれば, その点電荷の位置の被積分関数が0になるように積分式を立てて解き, 重ね合わせの原理を用いて,点電荷の電荷量だけ後から加算すればよい と思います. ーーーー引用終了ーーーーーーーーーーーー
>この積分式においては,原点の点電荷は考慮されていません.
という部分がありますが,ではこの積分が悪くて点電荷が入っていないようにも見えます.この積分は,遮蔽電場を作る電荷の積分であるという説明を明示的にしないと,質問側は自分のミスが在るかと誤解しかねません.
点電荷の解釈は各論があるようですが,特異性をあまりに全面に持ち出すのは誤解の元であるようにおもいます.むしろポテンシャル自体とか,電場自体の振る舞いから,素直に原点近傍の電荷を見いだすのが良いと思うようになりました.
いずれにしろ,質問者は,どこが悪いかも含めて質問している事を念頭においてくださると嬉しいです.また,質問する事自体,勇気のいる行為だと思いますよ.質問者さんには出来るだけ優しくしてくださいね.(今回は自分が質問者なので,調子がいいかもしれませんが....)
Re: 電荷密度を積分する場合
りんご さんのレス (2007/01/26(Fri) 18:00)
toorisugari no Hiroさん,
>そもそも大学1年にラプラシアン,しかも,極座標はないでしょう.だから,ご心配は杞憂です. ほっとしました.
皆さんの論議を拝見していて,デルタ関数には,もう少し工夫があるといいですね.
#質点等の論議は,いずれ余裕が在るときまでフリーズさせてください.
MXKさん,
素人から見ていると「MXKさんの解説は短すぎて判らない」と思っていましたが,今回のご解説には脱帽です.
>toorisugari no Hiroさんとの怒涛の議論の中心はそこにあるわけで,まだ宿題は残っています(よ).ガウスの定理を陽に使わないで,解析的計算だけで点電荷を出そうというわけです.
これはとても面白いアイデアだと思います.是非とも,解明されてパブリッシュされたら,ここで解説を付けていただけると幸いです.
>確認のために粗視化の手続きが必要になります.これによってデルタ関数が通常の関数になるので,従来の公式が自由に使えるようになります.(ただし,たたみこみ積分という,不慣れな道具だてが必要で,かなり重くなってしまいます.)
これもモンスタが他のモンスタに化けるだけなら困りますが,操作が人間の思考形態に自然な応答をするなら素敵でしょうね.
むしろ,フーリエ解析だ,ラプラス変換だで突っつかれたものの,あまりこれといった恩恵に浴せなかった凡人には,良い経験かもしれません.
Re: 電荷密度を積分する場合
toorisugari no Hiro さんのレス (2007/01/26(Fri) 18:01)
> toorisugari no Hiroさんとの怒涛の議論の中心はそこにあるわけで,まだ宿題は残っています(よ).ガウスの定理を陽に使わないで,解析的計算だけで点電荷を出そうというわけです.
「(よ)」って,私に対してなのですよね....(sigh)
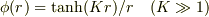 で計算したら,条件は満たすのですが,δ関数の形が汚いです.
で計算したら,条件は満たすのですが,δ関数の形が汚いです.
やっぱり,素直に
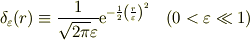
で三次元畳み込み 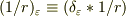 を計算しなきゃいけないような................
を計算しなきゃいけないような................
Re: 電荷密度を積分する場合
MXK さんのレス (2007/01/26(Fri) 18:17)
> 素人から見ていると「MXKさんの解説は短すぎて判らない」... 失礼しました.もうすこし舌をのばす努力をします.
>「(よ)」って,私に... 気づいていただいてありがとうございます.
3次元の2つの球対称関数のたたみこみ公式をまず作りたいですね. 教えていただいた文献の付録が参考になりそうです.
Re: 電荷密度を積分する場合
ミュフ猫 さんのレス (2007/01/26(Fri) 19:16)
>>この積分式においては,原点の点電荷は考慮されていません.
>という部分がありますが,ではこの積分が悪くて点電荷が入っていないように >も見えます.この積分は,遮蔽電場を作る電荷の積分であるという説明を >明示的にしないと,質問側は自分のミスが在るかと誤解しかねません.
仰るとおりです.すみません.電荷の符号を考えても,正の点電荷が含まれて いないことは,すぐに察しがつきました.しかし,電荷密度の式で定義されて いない点(つまり,原点)での被積分関数が0以外の値をとるような積分計算 のやり方は,直感でよくないような気がしたのです. つまり,原点に向かってマイナス無限大に発散する電荷密度の式では,積分の 取り方によっては,得られる結果の値がが変わるかもしれないと思いました. そこら辺を誤魔化しました.質問者に対して無責任でした. けんさん,ごめんなさい. 訂正したいですが,注意書きだけ加えて,自分への戒めのために残します.
なんか,どんどん恥の上塗りをしてる気がしてきました.(^_^;) ぜひ,何か間違いがあれば,どんどん言ってほしいです.m(_ _)m
ふと,思ったんですが,私のような低レベルのものはROMに徹した方が よいのでしょうか?高レベルの方で私にレスをつけてくださる方は, ごく僅かですし,デルタ関数の議論はちんぷんかんぷんで,点電荷の 導出方法に関することなのかも,理解できません.(ToT)
Re: 電荷密度を積分する場合
りんご さんのレス (2007/01/26(Fri) 20:18)
ミュフ猫さん,
>電荷密度の式で定義されていない点(つまり,原点)での被積分関数が0以外の値をとるような積分計算のやり方は,直感でよくないような気がしたのです.
私は,デルタ関数をつかった点電荷はある種の便宜上のものであると考えています.このスレッドの中にも書きましたが,電子は直径がゼロの質点とは思えません.
むしろ,極端に言えば,半径 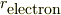 の粒子と考えた方が良いと思います.そうすれば,原点のでの特異性も,径がゼロの為に,r=0を特別視する必要も無いのではと思います.
の粒子と考えた方が良いと思います.そうすれば,原点のでの特異性も,径がゼロの為に,r=0を特別視する必要も無いのではと思います.
#この論議は良く他の方ともするのですが,もし原点での発散が本当に起るならば,荷電粒子はその巨大なクーロン電場で,自己放電をおこして崩壊してしまいませんか? #もしくは,水素原子で,s0の電子は,陽子の内側に侵入すると,その強力なクーロン力で二度と娑婆に出られなくなりませんか?
でも,これは普段には説明するのが面倒なので,よほどの事が無い限り,申し上げません.でも,今回は,すこし状況が特殊と考えてコメントしました.
ここら辺は,toorisugari no HiroさんやMXKさんの論議を拝見して行きたいと思っています.
>私のような低レベルのものはROMに徹した方がよいのでしょうか?
という意味では,このスレッド中でも,私は何度も計算ミスをしたり,極座標と円筒座標とを混同したり,原点近傍の電荷からの静電ポテンシャルへの寄与を誤解釈しました.
低レベルだからと言われると,私も出る番が無くなります.この掲示板のユニークなのは,色々な視点から,色々な論議が出て,段々と正解に近づくことです.面白いのは,その問題を知らない回答者が,これまでに知られていないような回答をだしたり,今回のように原点周辺の電荷を引き出す各種の方法が出てきたりしている事です.
従って,ミスを恐れて黙っているより,新しい解釈が生まれる事を期待して,自分の意見をぶつけた方が良いですよね.
>デルタ関数の議論はちんぷんかんぷんで,点電荷の導出方法に関することなのかも,理解できません.
と書いて置けば,どなたかがきっとコメントくださると思いますが....
Re: 電荷密度を積分する場合
ミュフ猫 さんのレス (2007/01/26(Fri) 20:35)
りんごさんへ
レスありがとうございます.間違いを指摘してもらえるのは幸せです. 私が恐ろしいのは,
「プッ.こいつまた,訳のわからん御託こいてやがる.めんどくせ.無視無視.」
こう思われるのがつらい.(だったら,書き込まなきゃいいのですが.w) 質問者は,無学でも許されますが,無学な回答者は「スレ荒し」を通り越して, 「笑われ芸人」となってしまいます. その意味で,私は質問者より,回答者の方が勇気がいると思います.
Re: 電荷密度を積分する場合
toorisugari no Hiro さんのレス (2007/01/26(Fri) 22:08)
> 私は,デルタ関数をつかった点電荷はある種の便宜上のものであると考えています.
誤解されているかもしれませんが,点電荷を,拡がりを持つ電荷におきかえても,理論からδ関数が消えることはありません.「微分」を使う限り. 「微分」を捨てるのなら,δ関数は消えますが,でも,「微分」を使わずに理論をどうやって記述すればいいのでしょう.
> #もしくは,水素原子で,s0の電子は,陽子の内側に侵入すると,その強力なクーロン力で二度と娑婆に出られなくなりませんか?
浅学にして,電子軌道S0の確率分布がクーロン力中心に特異点を持つ(電子が原点に束縛される)という計算結果は聞いたことがありません.
古典でも同様です.地球を「固定された立方体の頂点を構成する8個の点の組」(8個の質点が固定されている)だと考えてください.衛星軌道から質点を「地球」に向けてなげたら束縛されることがあるとお考えですか?(しばらく滞在することはありますが.)(点に衝突する場合は考えない方が簡単です.)
Re: 電荷密度を積分する場合
りんご さんのレス (2007/01/27(Sat) 00:49)
>誤解されているかもしれませんが,点電荷を,拡がりを持つ電荷におきかえても,理論からδ関数が消えることはありません.「微分」を使う限り. >「微分」を捨てるのなら,δ関数は消えますが,でも,「微分」を使わずに理論をどうやって記述すればいいのでしょう.
色々と考えてみましたが,どうやら素人思考では追跡不可能な領域と感じるようになりました.
現在のところ,自分の実際に興味のある分野では,デルタ関数を使う事が無いので,これ以上のコメントは差し控えたいと思います.MXKさんとの論議を拝見して,勉強させていただきたいと思います.
今回も,有益なご教示ありがとうございました.
Re: 電荷密度を積分する場合
りんご さんのレス (2007/01/27(Sat) 01:09)
ミュフ猫さん,
No.13779の修正を拝見しました.
私は,No.13909で,自分の考えをお伝えしましたが,
>>この積分式においては,原点の点電荷は考慮されていません. > >という部分がありますが,ではこの積分が悪くて点電荷が入っていないようにも見えます.この積分は,遮蔽電場を作る電荷の積分であるという説明を明示的にしないと,質問側は自分のミスが在るかと誤解しかねません.
と可能性をご指摘しただけで,ミュフ猫さんのご回答の全体が間違えであると思っていません.ただ誤解を受けやすいから,丁寧に説明されるといいなあ,と思ったのです.
それにしても,けんさんは大学1年生なのにとても鋭い質問をされて,我々も本当に勉強になりましたね.最後にけんさんの感想がお聞きしたいところです.
ミュフ猫さん,我々も,自分で判る範囲をリラックスして回答して行きませんか.
Re: 電荷密度を積分する場合
toorisugari no Hiro さんのレス (2007/01/27(Sat) 17:17)
MXKさん
該当するスレッドにつけようかとも思いましたが,ここで書きます.
> 不適切かどうかは講義など全体の文脈で判断するべきですから,質問者からの情報だけでは何ともいえません
そうですね.不用意な発言でした.(反省)
> じゃあ,一年生の解答例を考えましょうか;)
と言うより,あれが,本当に一年生向けに出されたものなら,たぶん,「(回転対称な系における)ガウスの法則と静電ポテンシャル・電場の関係式,および,電場・電束密度の関係式を使って,与えられた静電ポテンシャルから電荷分布( 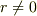 )および中心の電荷を求めなさい.」が本当の問題だったと私は思います.
)および中心の電荷を求めなさい.」が本当の問題だったと私は思います.
(正直,大学一年生(院じゃないですよね?)にくだんの問題を解かせるために,どのような講義体系を構成するのか,わたしには想像できません.ま,自分の昔の経験でいってるだけで,今の電磁気学の教育システムがよくわからないので何とも言えないのはたしかですが.)
もしそうだとしても,スレ主さんがその問題をポアッソン方程式で解こうとされたのが,誤解からなのか,自発的な発展学習なのか,スレ主さんがいらっしゃらないので,判断できませんけど.
(もちろん,質問の通りの出題の可能性もあります.そのときは,背景に興味がありますね.)
この問題は 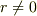 における,つまり多重連結領域におけるラプラス(ポアッソン)方程式の求解という,(学部学生にとっての)難問の一つですよね.
における,つまり多重連結領域におけるラプラス(ポアッソン)方程式の求解という,(学部学生にとっての)難問の一つですよね.
領域の外に特異点があってそれを考慮することで内部の解を得るという,電磁気学の鏡像法の考え方と同じですが,この問題の場合外部(境界?)が 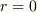 という点状であることが悩ましいところです.
という点状であることが悩ましいところです.
先に双極子だったら,という問いかけをしたのは,双極子は 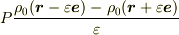 と点電荷が
と点電荷が 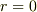 からはずれていると解釈できなくもないので,うまく解けるかなと思ったわけです.
からはずれていると解釈できなくもないので,うまく解けるかなと思ったわけです.
# よくかんがえれば,δ関数がでないのにその微分が出るわけないですね.
ええっと,宿題の方はゆっくり考えさせてください.何しろ,特殊関数が嫌い(わからない)ので,演算子法などに走った人間ですので.(今,そのツケの総額を計算しているところです.)
Re: 電荷密度を積分する場合
MXK さんのレス (2007/01/28(Sun) 14:44)
幾何学的には簡単に解けるのに,解析的に解こうとすると,特異性が うまく処理できず,行きづまるということですね.
積分型のマクスウェル方程式が重宝がられる理由の1つでしょう.
デルタ関数(+粗視化)を正しく用いれば,解析的手法だけで特異点や境界の 処理ができます.が,初等的とはいい難いところが問題です. うまく解けない問題があるのを理由に,微分型のマクスウェル方程式は 不完全という方もいますが,それは当たっていないと思います.
物理的には,金属やプラズマの中に点電荷  をおいた状況になっています.
遮蔽性能
をおいた状況になっています.
遮蔽性能 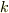 は媒質の導電率を反映するパラメータです.
遮蔽電荷の総量
は媒質の導電率を反映するパラメータです.
遮蔽電荷の総量  はもとの点電荷を取り除けば,
同時に消滅してしまいます.ですから定数項を含むのは当然です.
はもとの点電荷を取り除けば,
同時に消滅してしまいます.ですから定数項を含むのは当然です.
最後に求まる点電荷がむしろ発端なのです.
Re: 電荷密度を積分する場合
toorisugari no Hiro さんのレス (2007/01/29(Mon) 16:19)
MXKさん
> 積分型のマクスウェル方程式が重宝がられる理由の1つでしょう.
そうですね.初学者のときは,マクスウェル方程式の積分形が冗長で,微分形がシンプルに(わかりやすいではないです)見えて,「積分形なんて過去の遺物」だと思っていましたが,いろいろ学ぶにつれてそうではないことがわかってきました. でも,
> 微分型のマクスウェル方程式は不完全という方もいますが,
さすがに,それは思いません.場(各「点」にある量が記述される)と言う形式は近代物理学の基本であり,積分形は領域に対して定義されるという形式上,それとそぐわないですね.
場と言う概念が不明瞭になるがスカラー量で自然に定義できる積分形.「密度量」を導入することで「各点での量の記述」という場の概念が表現できる微分形....
後者は密度量と言う概念を入れたせいで,密度量の基底の一つであるδ関数を必然的に導入せざるを得ないと言う面があり,それが今回の議論につながっているわけですね.
Re: 電荷密度を積分する場合
yama さんのレス (2007/01/30(Tue) 17:05)
本題については一区切りついているようですが
># 計算していないので,わからないのですが,原点に双極子がある場合のポテンシャルを,極座標系のラプラシアンに(何も考えず)代入すると,ちゃんと双極子が現れるのかな?
というのが気になったので,偏微分方程式の本を参考に調べてみたところ,確かに双極子の電荷密度が得られることが分かりました.
まず,双極子 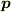 によるポテンシャルは次の通りです.
によるポテンシャルは次の通りです.
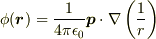 両辺のラプラシアンをとると次のようになります.
両辺のラプラシアンをとると次のようになります.
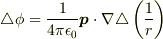 ここで
ここで 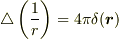 なので
なので
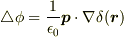 となります.
ポアッソン方程式
となります.
ポアッソン方程式 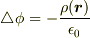 と比較すると電荷密度が
と比較すると電荷密度が
 となることが分かります.
これが確かに双極子の電荷密度であることは,次のように示せます.
原点に電荷 -q があり,点
となることが分かります.
これが確かに双極子の電荷密度であることは,次のように示せます.
原点に電荷 -q があり,点 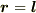 に電荷 +q があるときの電荷密度は
に電荷 +q があるときの電荷密度は 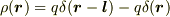 と表されますが,
と表されますが, 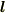 が微小であるとして
が微小であるとして 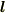 について展開して1次の項までを取ると
について展開して1次の項までを取ると 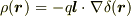 となります.
ここで
となります.
ここで 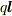 は双極子モーメントなので,
は双極子モーメントなので, 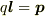 と置くと(1)式になります.
と置くと(1)式になります.
一般に超関数は何回でも微分可能なので,δ関数のさらに高次の導関数を用いることによって多重極の電荷密度を表すこともできると思います.
Re: 電荷密度を積分する場合
ミュフ猫 さんのレス (2007/01/30(Tue) 17:32)
静電場の電磁気学がこんなに難しいとは・・・.(ToT)
Re: 電荷密度を積分する場合
toorisugari no Hiro さんのレス (2007/01/30(Tue) 19:21)
yamaさん ありがとうございます.
ただ,問題は 「極座標系のラプラシアンに(何も考えず)代入すると」 なんですね.
> まず,双極子 |6ad36850d634705000b52803c62f2536| によるポテンシャルは次の通りです. >
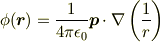
簡単のため 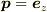 としましょう.
そうすると
としましょう.
そうすると
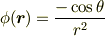
になります.(係数は無視しました)
これをラプラシアン
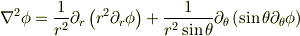
に代入すると,
0になってしまうんですね......
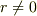 でしか意味がないから,当たり前と言えば当たり前なんですが...(でも,いけるのでは,と期待した理由は,前にも書きました.)
でしか意味がないから,当たり前と言えば当たり前なんですが...(でも,いけるのでは,と期待した理由は,前にも書きました.)
たぶん,極座標表示のラプラシアンでも何も考えずに,単極子・双極子が出るようにするためには  に現れる
に現れる 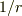 を普通の関数でなく超関数として扱わなければいけないのかもしれません.(これは粗視化することと同じ事です.)
を普通の関数でなく超関数として扱わなければいけないのかもしれません.(これは粗視化することと同じ事です.)
Re: 電荷密度を積分する場合
yama さんのレス (2007/01/30(Tue) 23:38)
極座標ののラプラシアンの式は r≠0 でしか成り立たないので,普通に計算したのでは双極子は出てこないでしょうね.普通の計算で 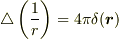 が出てこないのと同様でしょう.
普通の関数からδ函数を導くには,たとえば粗視化のように何らかの関数列の極限をとるとか,階段関数の微分のような形に持っていくとかが考えられますが,いずれにしても普通にラプラシアンの式で計算しただけではδ関数は出てこないと思います.
が出てこないのと同様でしょう.
普通の関数からδ函数を導くには,たとえば粗視化のように何らかの関数列の極限をとるとか,階段関数の微分のような形に持っていくとかが考えられますが,いずれにしても普通にラプラシアンの式で計算しただけではδ関数は出てこないと思います.
Re: 電荷密度を積分する場合
けん(大学1年) さんのレス (2007/01/31(Wed) 19:07)
レスしなくてすみません.途中からは知らないことばかりが出てきて,全く理解できなかったので,自分の疑問が解決されて,お礼を言った後,掲示板をあまり見ていませんでした.疑問は解決しました.ありがとうございました.
Re: 電荷密度を積分する場合
MXK さんのレス (2007/02/01(Thu) 23:39)
toorisugari no Hiro さん,yama さん,
粗視化は不可避のようですね. 円筒座標だと比較的簡単に階段関数が埋まっていることが分かります.
ダイポールのポテンシャルを円筒座標で表すと
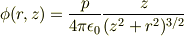
z軸上のポテンシャル 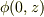 は原点で発散する.
しかし, z軸の近傍の半径
は原点で発散する.
しかし, z軸の近傍の半径  の円盤に関して
平均をとると有限にとどまる
の円盤に関して
平均をとると有限にとどまる
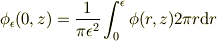
具体的に計算すると,  の正負に応じて
の正負に応じて
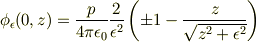
となり, 原点に跳躍が見えます.
Re: 電荷密度を積分する場合
toorisugari no Hiro さんのレス (2007/02/03(Sat) 18:16)
> 階段関数の微分のような形に持っていくとかが考えられますが,
わたしもそう思ってますが,確かめてなかったので単極子の場合をここで計算させてもらいます.
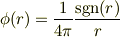
とおきます.ただし,  を正の微少量として,
を正の微少量として,
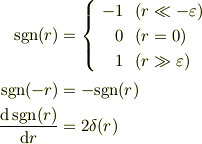
です.(ですから 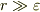 では従来の単極子の式と同じです.)
では従来の単極子の式と同じです.)
これを回転対称な場合のラプラシアンに代入すると,
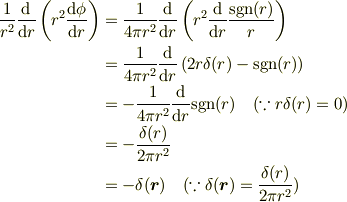
と確かに計算できますね. (ただ,この手の計算には落とし穴がありそうなので,ちゃんと計算するには粗視化が必要ですが.)
# あるいは出発点の式を
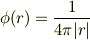
(ただし,絶対値は超関数として考える.
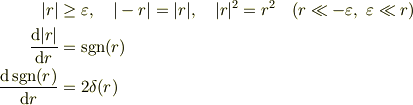
)と置く方がよいかな?
(これだと 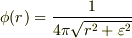 と粗視化する根拠も自明だし.)
と粗視化する根拠も自明だし.)
双極子は...追々考えます.
Re: 電荷密度を積分する場合
MXK さんのレス (2007/02/07(Wed) 13:40)
toorisugari no Hiro さん,
 が負の領域というのも気持ちが悪いので,
が負の領域というのも気持ちが悪いので,
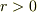 に限った方法の例を示します(半径
に限った方法の例を示します(半径 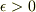 の球殻による粗視化に対応します).
の球殻による粗視化に対応します).
![\phi_{\epsilon}(r)=\left\{\begin{array}{ll}\displaystyle\frac{1}{4\pi \epsilon}& (0<r<\epsilon)\\[0.5em]\displaystyle\frac{1}{4\pi r} &(\epsilon\leq r)\end{array}\right.](http://hooktail.maxwell.jp/bbslog/0d65aaa9ffef1808a72d868e8fb49285.png)
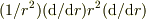 を作用させると,
を作用させると,
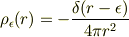
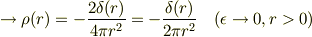
因子2は 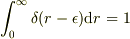 ,
,
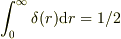 であることを
考慮したものです.
であることを
考慮したものです.
Re: 電荷密度を積分する場合
toorisugari no Hiro さんのレス (2007/02/07(Wed) 16:30)
MXKさん
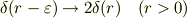
が若干気持ち悪いですね.
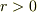 を考慮して自然に(積分を明示的に使わず)出ないかな?と考えたのですが,うまくいきませんでした.
を考慮して自然に(積分を明示的に使わず)出ないかな?と考えたのですが,うまくいきませんでした.
Re: 電荷密度を積分する場合
MXK さんのレス (2007/02/07(Wed) 21:41)
torisugari no Hiro さん,
説明のしかたはともかく, 球殻のもう一方の面(負の側)が重なってくる様子を想像すれば, 物理的にはきわめて自然だと思います.
Re: 電荷密度を積分する場合
yama さんのレス (2007/02/09(Fri) 17:21)
δ(r)を考えるとき,r>0 に限定すると取扱いが面倒になるので,r のとり方を変えて,r<0 も含めて考えてみました.もちろん,内容的には toorisugari no HiroさんやMXKさんの方法と実質的に同じことになります.
普通の極座標では 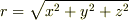 ですが,少し変更して
ですが,少し変更して 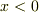 の場合には
の場合には 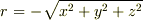 とします.
とします.
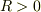 のとき,点
のとき,点 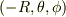 は,原点に対して点
は,原点に対して点 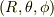 と対称な点を表すものとします.普通の表し方ではこの点の座標は
と対称な点を表すものとします.普通の表し方ではこの点の座標は 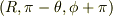 となりますが,2通りの表し方ができないように
となりますが,2通りの表し方ができないように 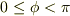 と制限しておきます.
普通の極座標では,
と制限しておきます.
普通の極座標では, 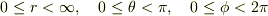 として全空間がカバーされますが,ここで考えた新しい極座標では,
として全空間がカバーされますが,ここで考えた新しい極座標では, 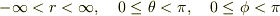 として全空間がカバーされます.
として全空間がカバーされます.
これに対応して 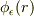 の定義も変更します.すなわち,MXKさんの定義式の右辺の
の定義も変更します.すなわち,MXKさんの定義式の右辺の  を
を 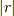 に変えます.
そうすると,
に変えます.
そうすると, 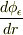 は
は 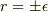 で不連続になります.そのため
で不連続になります.そのため 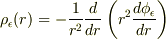 を計算すると次のようになります.
を計算すると次のようになります.
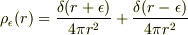 右辺第1項がMXKさんのおっしゃる「球殻の負の側」の電荷密度で,第2項が「球殻の正の側」の電荷密度です.
右辺第1項がMXKさんのおっしゃる「球殻の負の側」の電荷密度で,第2項が「球殻の正の側」の電荷密度です.
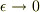 とすると
とすると
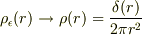 となります.MXKさんのおっしゃるとおり球殻の両側の面が重なるわけです.
となります.MXKさんのおっしゃるとおり球殻の両側の面が重なるわけです.
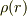 を全空間で積分する場合は,半球殻の体積
を全空間で積分する場合は,半球殻の体積 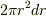 を掛けて
を掛けて 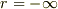 から
から 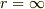 まで積分するので
まで積分するので 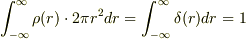 となります.
一方,普通の極座標系で
となります.
一方,普通の極座標系で 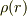 を全空間で積分する場合は,球殻の体積
を全空間で積分する場合は,球殻の体積 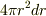 を掛けて
を掛けて 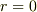 から
から 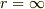 まで積分するので
まで積分するので 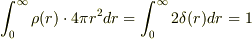 となり,上記の値と一致します.
従って,普通の極座標で考える場合も,電荷密度は
となり,上記の値と一致します.
従って,普通の極座標で考える場合も,電荷密度は 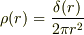 としてよいことになります.
としてよいことになります.
Re: 電荷密度を積分する場合
toorisugari no Hiro さんのレス (2007/02/15(Thu) 17:46)
以下の議論には問題があるので,withdrawします.
もういっかい考えなおさなきゃ....(sigh)
# 一次元のデルタ関数をベースに 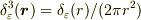 を使って考えてましたが,これでは特異点を除去(粗視化)したことにはなりませんね.
を使って考えてましたが,これでは特異点を除去(粗視化)したことにはなりませんね.
MXKさん > 「(よ)」って,私に対してなのですよね....(sigh) の宿題がやっとできました.
問題は以下の通りです. 「 δ関数は
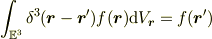
の性質を満たすが,δ関数に(弱)収束する回転対称な粗視化δ関数 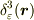
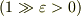 を用いて
を用いて
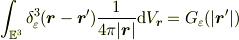
と与えられる 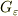 はどんな形になるか? 粗視化関数の具体的な形によらない議論をせよ.(なお,この
はどんな形になるか? 粗視化関数の具体的な形によらない議論をせよ.(なお,この 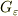 は
は 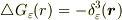 を満たすと予想される.)
」
を満たすと予想される.)
」
証明は非常に汚いので整理中ですが,結果は予想通り
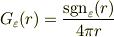
でした.ただし, 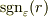 は滑らかな階段関数で
は滑らかな階段関数で
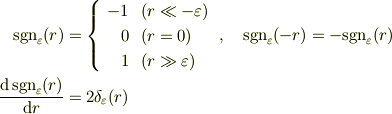
を満たすものです.正確には

であり,  として具体的には
として具体的には
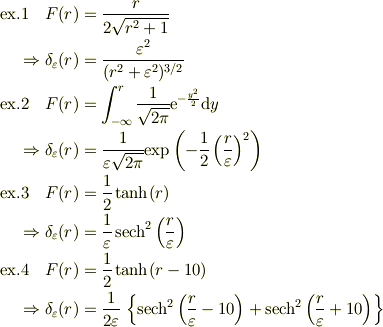
などです.
( 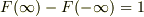 を満たし,かつ,滑らかな非減少関数(も少し制限を緩めてもいいかも)なら何でも良いです.また,微分したらδ関数の2倍になることさえわかっていれば,具体的な関数形は計算に必要ないです.)
を満たし,かつ,滑らかな非減少関数(も少し制限を緩めてもいいかも)なら何でも良いです.また,微分したらδ関数の2倍になることさえわかっていれば,具体的な関数形は計算に必要ないです.)
これを使って
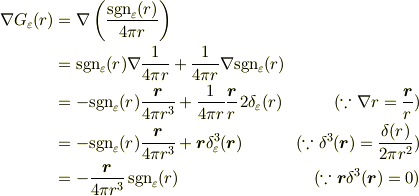
が得られ,さらに
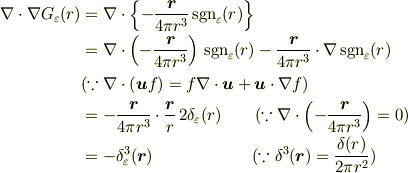
となり,
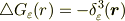
が得られます.
以前,極座標表示におけるラプラシアンの式に 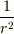 が含まれているので
が含まれているので 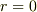 で式は意味をなさないから,中心の電荷が出ないと書きましたが,そうではなく,ポテンシャルの表式が
で式は意味をなさないから,中心の電荷が出ないと書きましたが,そうではなく,ポテンシャルの表式が 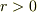 でしか定義されていないのが問題でした.しかし,上述のように階段関数を入れることで「形式的」に
でしか定義されていないのが問題でした.しかし,上述のように階段関数を入れることで「形式的」に 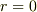 で意味をもつポテンシャル(グリーン関数)が得られ,議論ができます.
で意味をもつポテンシャル(グリーン関数)が得られ,議論ができます.
なお,
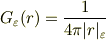
は双極子でうまく計算ができないので不採用です.(こちらの形の方が直感的には理解しやすいのだが...)