無題

home > 掲示板 >

このページのPDF版

サイトマップ

無題

けん（大学1年）さんの書込 (2007/01/04(Thu) 19:03)

質問させて下さい．

?保存力と中心力というのは，定義は全然違いますが，保存力だけど中心力でなかったり，保存力だけど中心力でないものは存在するんですか？

?正方形の各頂点に同じ大きさの点電荷q(>0)を置きます．4点A(a,0),B(0,a),C(-a,0),D(0.-a)に置いたとします． Aから出る電気力線の中に，原点向きのものがあると思います．これはx>0では，真っ直ぐ原点に向かって進みます．ですが，原点では，力のつりあいから，電場が0になると思われます．では，今考えていた電気力線は原点付近まで真っ直ぐ引かれたあと，どうなっているのでしょうか？

?電気力線の密度に関してです．閉曲面の微笑部分を考える．この微笑部分は平面と，電場Eは一定と考えてよい．微小な面Sの法線をnとする．微小な面Sの面積をS，Sを貫く電気力線の数をNとする．Eとnとのなす角をθとする．

このとき，微小面Sでの電気力線の密度はN/Scosθ と書いてあります．

Sを貫く電気力線はN本ですから，Sに垂直な成分はNcosθになるとも思いました．すると，電気力線の密度はNcosθ/S になってしまいました．この考え方はどこがおかしいのでしょうか．

?P点を通る等ポテンシャル面をとる．P点で等ポテンシャル面に法線を引き，その上にP'をとる(PP'=s)．P点から法線にそってsだけ離れた点，すなわちP'の電位をφP(s)とすると，

Ep=-lim(s→0)(φp'-φp)/s =-dφp(s)/ds 電場の向きは等ポテンシャル面に垂直で，ポテンシャルの減少する方向である．

と書いてあります．「電場の向きは等ポテンシャル面に垂直」は分かるんですが，「ポテンシャルの減少する方向である」が分かりません．どうして増加する方向ではなく減少する方向というのがこの式から分かるのか，教えて下さい．

?q∫(P→O)(E・t)ds は，pからOに戻る時に電荷が外に対してする仕事である．と書いてありますが，「電場E」がする仕事と言ったらいけないのでしょうか．

以上，多くて申し訳ありませんが，よろしくお願いします．

Re: 無題

りんごさんのレス (2007/01/04(Thu) 21:23)

初めまして．沢山質問があるので，説明できる所だけを書いてみます．なお，丸に数字の文字は，文字化けしやすいので(n)の表記にします．

地表の重力場は，近似的ではありますが，保存力でありながら中心力ではないと考えられますね．電場駆動型のCRTでの電子は，事実上保存力系ですが，中心力ではありませんね．逆にバネ系は保存力で，中心力でもありますが，摩擦力がはいってしまうので保存力にはなりにくいでしょう．もちろん理想化したバネなら良いでしょう．
お説の様に，対称性から中央に電場は存在しませんから，電気力線も到着できないと考えると思います．むしろ，2電荷の系を考えて，同一符号の2電荷の場合と，逆符号の2電荷の場合とから考え直すことをお勧めします．

(3)私は，ある点を通る電気力線を考える事はできますが，その本数をどうやって定義し，その面数密度をどうやって定義するのか存じません．電荷に関するガウスの法則，その積分法則などでは，電場の面積分を計算しますが，それと電気力線の数と直接的に関係する先験的な理由はないと思っています．これについては，異論が多数あるとおもうので，そちらを詳しくご検討ください．

式の表記法が良くわかりませんので，回答できません．
上に同じ．もし，どこかのサイトに表記の説明があれば，ご紹介ください．

Re: 無題

yama さんのレス (2007/01/04(Thu) 23:26)

りんごさんがあまり書かれなかった部分について簡単に書いておきます．

? 電気力線の密度は，Ncosθ/S が正しいと思います．

? Ep の式の右辺にマイナスの符号がついているためです．これがプラスだったらポテンシャルが増加する向きになります．

? 「電場E」がする仕事というのが正しいと思います．電荷が外に対してする仕事に等しくなることもありますが，常にそうなるわけではありません．

Re: 無題

ろむさんのレス (2007/01/05(Fri) 00:47)

電気力線の密度は N/Scosθ が正しいと思います．ひとまず自分が高校の時に [引用] 電界の強さがＥ[N/c]のトコロでは，電界に垂直な断面を通る電気力線を1m^2あたりＥ本の割合でひくものとする（理論上のことで，実際に描くときは適当でよい [物理のエッセンス(新課程対応改訂版)電磁気・熱・原子p11] と習ったことを記します．物理のエッセンスというのは私が大学入試の時に使っていた参考書です．入試の物理を扱う一般的なものの一つだと認識しています．また，ガウス平面の極小面積を次の様に考えます．その面積はけんさんに従い・極小面積は平面である・極小の面積をSとする・極小面積を通る電界vector(Ｅ)は一定である・極小面積に垂直なベクトルvector(n)を考える・vector(E)とvector(n)のなす角をθとする・極小面積を通過する電気力線の総数をNとするとしますが，さらに極小面積が正方形だと考えてみてください．以上を考慮に入れて?を自分なりに考えてみました．

まず三次元のデカルト座標(？直交座標)を考えます． vector(E)を原点から始まりZ軸に向くとします． vector(E)とvector(n)は角度θをなすので，極小面積とxy平面も角度θをなします．（この時，正方形に定めた極小面積の一辺をｙ軸またはz軸に平行になるように極小面積を配置すると考えが楽です）この時，極小面積を通過する電気力線は，極小面積をxy平面に射影した部分の面積も通ります．極小面積をxy平面に射影した部分の面積はScosθですその面積にN本の電気力線が通っているので，電気力線の密度は N/Scosθ だと思います． Ncosθ/Sだと，先ず本数のNをコサインに掛けるということが不思議に思いました．

横槍すみませんでした．俺が答えることでりんごさんyamaさんの意向を乱すようでしたらそれについても侘びさせていただきます．

Re: 無題

りんごさんのレス (2007/01/05(Fri) 02:59)

ろむさん，

>俺が答えることでりんごさんyamaさんの意向を乱すようでしたらそれについても侘びさせていただきます．

少なくとも，私は問題ないですよ．むしろ私は，「電気力線の数を出す意味がないという」主張をしている少数派ですから．

一応，私の意見を補強しておきます．いまから40年ほど前には，私も電気力線に興味があり，いろいろ調べました．その結果，電気力線の数密度を出せるとすれば，『金属導体の形状が確定して，それらに一定の静電荷が与えられて，その境界問題が解かれてはじめて電気力線が与えられる』という結論です．

問題が解かれているのに，一々，電気力線の数密度をだしても無意味であるというのが私の結論でした．その代わりに，次のイメージを持つようにしました．

・単独電荷Qからは，クーロンの法則によって電場が発生して，無限大遠方にまで続きます．当然，電気力線は無限まで直線的に，かつ距離の逆自乗法則に従う訳です．座標原点に電荷を与えた場合，

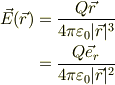
$\vec E(\vec r) &= \frac{Q\vec r}{4\pi \varepsilon_{0} |\vec r|^3}\\&=\frac{Q\vec e_{r}}{4\pi \varepsilon_{0} |\vec r|^2}$

・これを半径Rの導体球に電荷Qを与えて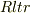， R lt r となる球殻について，ガウスの発散積分を適応すれば，

$\int_{r \mbox{Sphere} S=4\pi r^2} \vec E(\vec r)\cdot \vec e_{r} \mathrm{d}S = \frac{Q}{\varepsilon_{0}}$

この式で着目するべきなのは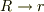， $R \to r$ としても同じ値を示します．言い換えると，導体球Rの外側にできる電場は，仮想的にその半径rの導体球の電荷から派生する電荷面密度 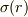$\sigma (r)$ により与えられる：

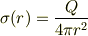
$\sigma (r)= \frac{Q}{4\pi r^2}$

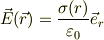
$\vec E(\vec r) = \frac{\sigma(r)}{\varepsilon_{0}} \vec e_{r}$

逆に言えば，ある強度の電場が存在して，ある金属(法線ヴェクタ 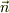$\vec n$ に入り込む場合には，当然電場は垂直に入射するので，金属には少なくとも

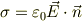
$\sigma = \varepsilon_{0} \vec E \cdot \vec n$

の表面電荷が発生している．

こう考えると，難しい「電気力線の数密度」を詳細に論議する必要がないと思えるのです．

取り急ぎ，書いてみたので，おかしな点があると思いますが，感じはこんな所です．

また，マクスウェルの方程式群を熟知されている方からみれば，何の事はない，静電場のガウスの法則そのものではないかと仰ると思いますが，まさにそうです．でもわざと，クローロンの法則とガウスの発散積分とから出しているので，初心者の方のイメージ作りに好適かと思います．

Re: 無題

yama さんのレス (2007/01/06(Sat) 09:00)

ろむさん，りんごさん，御意見ありがとうございます．お二人が書かれたことを参考にして考え直してみたところ，電気力線の密度を Ncosθ/S としたのは，間違いだったようです．電気力線の密度は単位面積当たりの本数ですが，面積S当たりN本なので，密度は単純に考えて N/S になると思います．もちろん電気力線に垂直な面について考えると，密度は N/Scosθ になりますが，これはあくまでも電気力線に垂直な面における密度であって，面Sにおける密度ではありません．また，電気力線に垂直な面における密度が電場の強さに対応していると考えると，面Ｓにおける密度はＳに垂直な電場の成分に対応すると考えることができそうです．この考え方では，電気力線の方向の大きさ N/Scosθ のベクトルを面Sの法線方向に射影したものが Sにおける密度になると思いますが，これも (N/Scosθ)×cosθ=N/S になり，上記の値に一致します．

電気力線の本数というのは，数学的に曖昧な点ははありますが，ガウスの法則を直観的に理解するための補助的便宜的なものとしては役に立つと思います．

Re: 無題

ろむさんのレス (2007/01/06(Sat) 11:47)

>>電気力線に垂直な面における密度であって，面Sにおける密度ではありません．失念していました．以後精進します．

Re: 無題

yama さんのレス (2007/01/06(Sat) 12:10)

私も初めは，電気力線に垂直な面における密度が N/S であると誤って考えていたので，ろむさんの御指摘がなければ誤りに気づかないままだったでしょう．気づいたことは遠慮なく書き込んでいただければいいと思います．どうもありがとうございました．

Re: 無題

りんごさんのレス (2007/01/06(Sat) 13:49)

yamaさん，

>電気力線の本数というのは，数学的に曖昧な点ははありますが，ガウスの法則を直観的に理解するための補助的便宜的なものとしては役に立つと思います．

任意に電気力線の数Nを決められて，その上どのようなイメージが増やせるのか，理解できません．また，そんなに有効な手法ならば，問い(2)を電気力線の数の観点からご解説いただけませんでしょうか？

さらに，もしよろしければ，電気力線を用いて「ガウスの法則を直観的に理解するための補助的便宜的」に解説している図書をご存知でしたらお教えくださいませんか？

Re: 無題

yama さんのレス (2007/01/06(Sat) 17:07)

>任意に電気力線の数Nを決められて，その上どのようなイメージが増やせるのか，理解できません．また，そんなに有効な手法ならば，問い(2)を電気力線の数の観点からご解説いただけませんでしょうか？

電気力線が正電荷から出て負電荷に入るとか，正電荷から出て無限遠に向かって広がっていくなどいろいろなイメージを思い描くことができると思います．たとえば次の問題もこのようなイメージで考えることができると思います．

http://hooktail.maxwell.jp/cgi-bin/yybbs/yybbs.cgi?room=room1&mode=res&no=13445&mode2=preview_pc

問い(2)についてですが，これは特定の電気力線のふるまいに関するものなので，電気力線の数には関係ありません．従って，残念ながら電気力線の数の観点から説明することはできません．

>さらに，もしよろしければ，電気力線を用いて「ガウスの法則を直観的に理解するための補助的便宜的」に解説している図書をご存知でしたらお教えくださいませんか？

高校物理の教科書や参考書では，電気力線を用いてガウスの法則を説明しています．この場合は電気力線は補助的というよりもむしろ主体的な役割をするわけですが，大学できちんとした数学的定式化で学ぶ場合に，高校物理で学んだイメージが補助的なものとして役立つと思います．

Re: 無題

りんごさんのレス (2007/01/06(Sat) 18:02)

>電気力線が正電荷から出て負電荷に入るとか，正電荷から出て無限遠に向かって広がっていくなどいろいろなイメージを思い描くことができると思います．たとえば次の問題もこのようなイメージで考えることができると思います．

http://hooktail.maxwell.jp/cgi-bin/yybbs/yybbs.cgi?room=room1&mode

=res&no=13445&mode2=preview_pc

これを拝見しても，電気力線をイメージして理解できますが，その電気力線の数の密度分布から云々しているとは思えません．

何度も言わせて戴きますが；

・電気力線をイメージできても，・電気力線の数密度をイメージするのは極端に難しい．・そんな難しい事を考えるなら，電場の強度を考えた方が解りやすい．

>高校物理の教科書や参考書では，電気力線を用いてガウスの法則を説明しています．

なんで，そんな無駄な教育をするのでしょうか？「クーロンの法則」と「静電場のガウスの発散積分の公式」だけで割り切れば，抽象的な「電気力線の数密度」は完全に不要とおもいます．

逆に，中途半端な，ベクタでもスケイラでもなさそうな「電気力線の数密度」が頭にあると，通常のベクタ解析をマスタして，いざ「静電場のガウスの微分の法則」を勉強しようとする学生さんは高校から習った「電気力線の数密度」と折り合いを付けるのに不毛な労力が掛かるのではありませんか？

本当に電気力線がなけれ電場が理解できないのならば，磁石が作り出す磁場の理解はどうなるのでしょう．「磁力線の数密度」なる量を考えて行くのでしょうか？

Re: 無題

kei さんのレス (2007/01/06(Sat) 21:17)

はじめまして

ふらふら〜っと，ページを眺めていたのですが大学で電気工学を専攻している手前気になったので書き込みさせていただきます．

りんごさん，高等な数式もご存知のようなので，かなりこの方面にお強いのだと存じます．

さて

> ・電気力線をイメージできても，・電気力線の数密度をイメージするのは極端に難しい．・そんな難しい事を考えるなら，電場の強度を考えた方が解りやすい．

とありますが，電気力線について訂正させていただきます．

電気力線も電界強度もダイレクトに測定できません．高校の教育過程でいうなら計れるのは，簡単な計器で距離，面積，電気量ぐらいでしょう．ここで，電界強度を定式する際にこの３つでもって式を構築しなくてはなりません．

計算式としては僕の知る限りでは電気力線"自体"を式で定義しているものは見たことがありません．代わりにこの電気力線の本数を定義します．

ある面素の面積(ベクトル)をdSとおく．この面素をとった空間には電界(ベクトル)Eが存在しているものとする．このときdSを貫く電気力線(以下，力線)の本数dNを次式で定義する．

dN = E・dS (1)

静電場におけるガウスの法則は，ご自身が書かれている通りでこれが正しいものとして話を進めます．(1)式の両辺を積分して全力線本数Nを求めましょう．

N=∫dN = ∫E・dS = Q/ε0 (2)

この左三つが(1)を積分した結果で右二つが，ガウスの法則です．この積分は電荷を囲むような閉曲面の存在があって初めて実行可能ですがこれを満たした上で(2)式をじっくり眺めて見ましょう．まず最右辺と最左辺から力線本数と電気量が比例関係にあることが分かります．測定できる電気量でもって力線数を定量化することに成功したことを意味します．また，全力線本数はガウスの法則とイコールでつながれていることも重要です．

続いて力線数密度について考えて見ます．実はこの言葉を聞いたのは初めてで定義がいまひとつ分からないので皆さんが使っている

(力線数密度) = (力線本数)/(力線が貫く面積)

を利用させて頂きます．(1)式を定義したときの文字を利用してやれば

(力線数密度) = dN/|dS| = E・dS/|dS| = Ecosθ(3) [ただしθはEとdSのなす角とする]

と計算できます．なので力線数密度は電界の面素dSに直行する成分であることが示されます．式の上では力線数密度と電界が等価なので考える上でもこの２つがリンクしていないとマズイことになります．

ある変形することの無い面素をイメージしてください．そこに2,3本しか電気力線が通っていない場合(A)と，同じ面に数百本通っている場合(B)を考えましょう．面素は変形せず面積は一定なので，Aが力線数密度が小さい場合，Bが力線数密度の大きい場合であることは理解いただけると思います．(3)式から電界と力線数密度は数値上で比例しているのだから

A→力線数密度小→電界小(力線がスカスカだと電界が小) B→力線数密度大→電界大(力線が詰まっていたら電界は大)

と対応付ければ合理的である，という答えでいかがでしょうか?

>磁石が作り出す磁場の理解はどうなるのでしょう．「磁力線の数密度」なる量を考えて行くのでしょうか？

磁界の考え方は発展させるとそうは言えませんが，おおよそ電界とおなじ定式法をしていきます．なので磁力線本数をMと空間内の磁界(ベクトル)をHと置けば

静電界：N=∫dN = ∫E・dS = Q/ε0 (2) 磁界：M=∫dM = ∫H・dS = 0 (4)

とかけます．電磁気では(2)と(4)をあわせてガウスの法則と呼びます．微分形はQ=∫ρ dvと書いてベクトルの公式を適用して

静電界：div E = ρ/ε0 (2)' 磁界：div H = 0 (4)'

で書き表せます．

Re: 無題

ミュフ猫さんのレス (2007/01/06(Sat) 22:24)

keiさんはじめまして

>力線数密度は電界の面素dSに直交する成分であることが示されます．

ということは，力線数密度の大小でわかることは，電場のある方向成分の大小に限られる訳ですよね？その情報だけで，スカスカとか想像しにくい気がするのですが．ただ，電場の強弱を作図で考えるとき，無意識に「→」の数を増やして書き込むことをよく行いますので，電束や磁束の概念はある意味，有益ではないかと思います．

Re: 無題

りんごさんのレス (2007/01/06(Sat) 22:28)

keiさん，初めまして．

>電気力線も電界強度もダイレクトに測定できません．高校の教育過程でいうなら計れるのは，簡単な計器で距離，面積，電気量ぐらいでしょう．ここで，電界強度を定式する際にこの３つでもって式を構築しなくてはなりません．

自分でやった事はありませんが，高校の理科室にあるような高電圧発生器の電極に細かな糸でも接着しておけば，電場の方向は測定できますし，電圧計をつけられれば原理的には電場も決められます．

また，近くのスレッドにホール電位の話がありますが，磁場と電子銃，電子の位置検出器を組み合わせた系を考えれば，原理的には電場を決定できます．物理の問題として考えるときに，原理的可能性だけが問題であり，もし原理的に測定できないのならば，物理の対象になり得ないとおもいます．

さらに言えば，クーロンの法則の直接測定では，一定電位にチャージした電極間にかかる力を測定していますよね．

>高校の教育過程でいうなら計れるのは，簡単な計器で距離，面積，電気量ぐらいでしょう．ここで，電界強度を定式する際にこの３つでもって式を構築しなくてはなりません．

したがって，高校生だからこのような物理量に限定すると，逆にクーロンの法則が困ってしまいませんか？

Re: 無題

MXK さんのレス (2007/01/07(Sun) 00:05)

電気力線の数は本質的な概念なので追い出す訳にゆきません．例えば，点電荷のつくる電場が遠方で弱くなるのは，電気力線の数が疎になるからです．実際上は教科書の扱いにかなり混乱があって，奇妙なものように思われがちですが，ファラデー以来の概念を易々と放棄することはできないでしょう．注意すべきポイントは <pre> * 電場ではなく，電束や電束密度に関する概念である． * 数を数えるためには単位を指定する必要がある． * 整数とは限らない． </pre> これに関しては，以前この掲示板で議論がありました．

http://hooktail.maxwell.jp/bbslog/11611.html

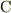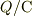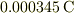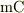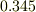そこでも述べたように，「電荷から,クーロン $\mathrm{C}$ を単位として, $Q/\mathrm{C}$ 本の電束管が出ている．」「 $0.000345\,\mathrm{C}$ の電荷からは， $\mathrm{mC}$ を単位として, 0.345 本の電束管が出ている．」などが正確な表現です．電気力線の数に関しては，ほとんどどの教科書でも触れられています．あえて例を挙げるなら，太田：電磁気学I p.47，今井: 電磁気学を考える p.8．

Re: 無題

yama さんのレス (2007/01/07(Sun) 00:08)

>これを拝見しても，電気力線をイメージして理解できますが，その電気力線の数の密度分布から云々しているとは思えません．

「円柱面上に電荷が分布している場合は，電気力線は円柱面に垂直に２次元的に広がるので，電気力線の密度は円柱の中心からの距離に反比例することになります．」と書いてある通り，電気力線の密度について述べているのですが・・・．

確かに「電場の強さがEのところで単位面積当たりE本の電気力線」といってもイメージが湧きにくいですね．その意味では電気力線の密度を用いないでガウスの法則をを学ばせようという考え方にも一理あると思います．しかし，高校物理ではそれは難しいと思います．というのは，そのためには微積分の理解が前提になると思いますが，微積分を含む数学の科目は必修ではないし，履修するとしても物理の履修の前に微積分の履修が終わっているとは限りません．従って，教科書も微積分の理解を前提としないで書かれているわけです．電気力線の密度というものが中途半端なものであることは高校生も分かっていると思います．単位面積当たりE本の電気力線というのは，あくまでも便宜上考えた仮想的なものであって，実在するものだとは考えないと思います．もしそのように誤解したとすれば，教え方が悪いというべきでしょう．問題は大学での教育です．大学では数学的にきちんとした形で理解させるのは当然ですが，高校物理の内容を無視していきなりベクトル解析などで説明したのでは，学生は高校の学習内容との関連が分からずに混乱すると思います．高校物理との関連を十分考えて，電気力線の密度も補助的に用いるなどしながら数学的にきちんとしたものに定式化してゆけば，折り合いを付けるための不毛な労力も不要になると思います．

また，前に書いたように電気力線は電場の様子を直観的に理解するのに役立ちます．たとえば電気力線の図を見れば電場の向きは容易に分かるし，電気力線が密集しているところは電場が強いということから，電場の強さもある程度分かります．電気力線の密度を文字通りの意味に考えないで，keiさんが述べられているような抽象的な意味に考えれば積分形式のガウスの法則との対応もより明確になると思います．従って大学においても電気力線を考えるのは有益だと思います．

Re: 無題

なんとなくさんのレス (2007/01/07(Sun) 00:23)

みなさん，こんばんは．

いろいろ意見が出ているようなのですが，私にはyamaさんの考えが至極全うであると思えます．電気力線は磁力線が磁場の向きと強さを「視覚的に」分かり易くするための「デザイン」であると同様な意味で，（場所による）電場の強さを視覚的に表す「デザイン」以外の何物でもないと思います．勿論，本当は連続的に変化する「場」は無限階の彩色で表現すればさらに良いでしょうが，面倒過ぎます．何より，議論中にも混乱が見られますが，電気力線は物理量ではなく，補助単位でもありません．直接・間接測定の議論も定義が曖昧ですが，電気力線の功罪が問われるなら，それは偏にデザインの善し悪し，つまり「電場の理解を却って誤らせる」類のデザインかどうか，と言う点のみです．一応本数の引き方に約束はありますが，では１Ｃの単極電荷で何本引かなければならないか！・・・意味の無いことです．あくまで線の混み具合の比較により「一枚の図」の中では同じルールに従う，ことに意味があるのみでしょう．その意味でyamaさんは数学的に曖昧と表現されているのでしょう．磁力線，磁束はよく砂鉄で磁石の周りの磁場を視覚化する小学生向けの実験がありますが，ちょっと複雑な電場の電気力線など，この応用問題に過ぎませんし，イメージ化として決して悪いものとは思えません．電気力線の密度など，上記のことを考えれば，おのずと立場は明らかです．電場におけるガウスの法則の説明は任意の閉曲面で証明されますが，この表面は別に導体でもなんでもなく，仮想的な２次元曲面です．電荷分布とか，垂直に入るなどとは別問題です．その本質は電場の強さが内部空間のソース（湧き出し，吸い込み）に比例することを言っているのだと思います．蛇足ですが，ついでに言えば，原理的に観測できない波動関数は物理量ではありませんが，物理学の対象ではあります．しかし，この場合でも間接的に存在（確率密度）が観測可能量であるわけです．ただし，その実在性については物理学以外に形而上学的問題を含むため，一概には結論できませんが．

Re: 無題

yama さんのレス (2007/01/07(Sun) 00:53)

なんとなくさんのおっしゃるように電気力線はデザインであるとも言えますが，「接線が電場の向きであるような曲線」と定義されているので，数学的にも物理的にもきちんとした意味をもっていますし，方程式で表すこともできます．すなわち，接線方向の単位ベクトルと電場の方向の単位ベクトルが等しいことから 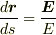$\frac{d\bm{r}}{ds}=\frac{\bm{E}}{E}$ と表されます．この定義によると，電場が0でない任意の点を通る電気力線を考えることができるので，電気力線は無限にあることになります．しかし，電気力線の本数という場合は，MXKさんが述べられているように電束管に関連させて考えるのが妥当だと思います．

Re: 無題

りんごさんのレス (2007/01/07(Sun) 01:59)

MXKさん，

「電磁気学を考える」は，逆の目的から入手したものの読んでいません．

でも，p８には；

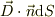ある法線ベクトル $\vec n$ の面積要素 $\mathrm{d}S$ を貫く電気力線の数は， $\vec D\cdot \vec n \mathrm{d}S$ ，である．ここでベクトル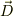， $\vec D$ は，電束密度である．

と明記されています．

基本的に，上記の解釈ならば，私も異議を唱えません．特に初学者が「真空に付いての電磁気学を学び始め」は電場と電束密度は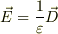， $\vec E = \frac{1}{\varepsilon}\vec D$ です．

他方，最近の大学での教育では，電磁気学を学んだ後に流体力学を教えるようです．むしろ，「Back to Faraday」は，ある種の専門的な電磁気，たとえば，電磁流体力学を徹底的に研究するとかの特殊分野になるように思います．

むしろ，高校生さんたちに解りやすく電磁気を教える観点から，どうすれば良いのでしょうか？

例えば； <pre> ・点電荷のクーロンの法則・球殻に広げた電荷の +遠方での振る舞い， +球殻内部でのゼロ電場・二重球殻での振る舞い +球面の微小面から出る電場は，微小面の法線ベクトルを向き，そこの電荷面密度に比例する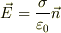； $\vec E = \frac{\sigma}{\varepsilon_{0}}\vec n$ ・二重球殻→二重平面→二重同芯筒

</pre>

といった展開を用意すれば，普通の電磁気学でもマクスウェル方程式なしで，静電場は説明できるようにも感じます．

＝＝＝＝＝＝

yamaさん，

>「円柱面上に電荷が分布している場合は，電気力線は円柱面に垂直に２次元的に広がるので，電気力線の密度は円柱の中心からの距離に反比例することになります．」と書いてある通り，電気力線の密度について述べているのですが・・・．

何度か拝見しているので，私は理解できます．でも，球→平面→円柱との関連つけをするには，空間把握，とくに対称性の観点から解りやすい説明をしないと，初学者には，解らないのではないかと思います．

私は，yamaさんは数学ができない生徒の存在が理解できないのではないかと思っています．その点，私は，正真正銘の「数学おちこぼれ」なので，自由度の違いと電気力線の関係をすぐに理解できなかったので...．

「電束管」に拘られていますが，ある微小領域の面の一周の線上から電気力線をチューブ状につなげたと考えても良いですよね．日頃親しんでいる，電場をわざわざスポイルする根拠が判りません．

Re: 無題

りんごさんのレス (2007/01/07(Sun) 02:27)

keiさん，

電場の測定法の一つですが，上でMXKさんが言及された図書；

「電磁気学を考える」，今井功・著，サイエンス社，ISBN4-7819-0572-2

のp15, 図6に対抗コンデンサがバネ(導体)で繋がれています．そのバネの変位測定で電場強度を計る提案がありましたよ．

この方法では，絶対値しか判りませんが．

Re: 無題

yama さんのレス (2007/01/07(Sun) 10:07)

>何度か拝見しているので，私は理解できます．でも，球→平面→円柱との関連つけをするには，空間把握，とくに対称性の観点から解りやすい説明をしないと，初学者には，解らないのではないかと思います．

私はできるだけ質問者自身に考えてもらおうと思っています．そのため，きちんとした模範解答を与えるのではなく，質問者が考えるのを助けるような回答をするようにしています．だから，回答はあまり詳しく書かないで，場合によってはヒントだけを与えるようにしています．回答として書かれていることの行間を読みとったり，回答をもとに自分自身で考えることによって考える力がつくと思うからです．もちろん，回答をもとに考えても分からない場合もあるでしょう．その場合はどのように考えてどこが分からないかを書いて再質問してもらえば，それに対してまた回答することになります．

この質問の場合は，簡単な回答で理解していただいたようなので，詳しい説明はしなかったのですが，もし再質問があれば，対称性の観点からの説明もしたでしょう．

>「電束管」に拘られていますが，ある微小領域の面の一周の線上から電気力線をチューブ状につなげたと考えても良いですよね．日頃親しんでいる，電場をわざわざスポイルする根拠が判りません．

もちろん，基本となるのは電場だと思います．電束とか電束管は電気力線の密度というものを意味づけるための補助的概念だと考えています．

Re: 無題

MXK さんのレス (2007/01/07(Sun) 10:20)

電場には，E, D に代表される下記のような二面性があります．

<pre> 機能量単位ルール幾何的表現力を与える EN/C = V/m curl E =0 等電位面ソースとの関連 DC/m^2 div D = rho 電束管 </pre>

流体でいえば，前者は流速場，後者は流量場に相当します．これらは相補的なもので，どちらが主，どちらが従というものではありません．

幾何学的には等電位面と電束管がつくる3次元的なメッシュが電場の総体を表しているといえます．2次元静電場の場合は等角写像を表すメッシュ(u=一定，v=一定)が幾何学的表現になります．

電場は矢印で描けばいいのではと仰っていますが，矢印は局所的なもので，法則の制約なしに自由に描けてしまいます．実測結果や計算結果の図示にはいいかも知れませんが，電場のルールを知る上ではあまり役に立ちません．

Re: 無題

なんとなくさんのレス (2007/01/07(Sun) 11:24)

少し誤解を招きやすい表現だったかもしれません．勿論，電気力線，電束，電束管は物理（数学）的に定義され，電場，電荷，電位などの「物理量」と同じく物理的概念です．しかし，また語弊の問題は否めませんが，後者が実在する物質のあるいは空間（言い換えれば客観的存在）の属性であるのに対し，前者はそれを説明する人為的概念ではないでしょうか．その意味で「デザイン」と称したわけです．私が言いたかったのは繰り返しになりますが，議論の中心点はこの概念を使うことの妥当性，または不当性に絞らないと，議論自体の意味が無いのではないかと言うことです．議論を読み返しても元の問題?の解答にヒントになっているのか不明ですが(^^;)，ひとつだけ言うと，上記の私の立場から見れば，あたかも電気力線が初めに存在し，その原点に向かうものが途中消失するので，どこへいったのか？と問うているように思えます．しかし，電場があってそれを表現するのが電気力線ですから，原点に向かうような線は「あるはず」ではなく，「描かない」が作法に近いと考えます．なぜなら，力線の書き方として，途中で交わらない，切れない，という約束事に反するからです．

Re: 無題

ミュフ猫さんのレス (2007/01/07(Sun) 11:33)

MXKさんはじめまして

>電場は矢印で描けばいいのではと仰っていますが，矢印は局所的な >もので，法則の制約なしに自由に描けてしまいます．実測結果や計算結果の >図示にはいいかも知れませんが，電場のルールを知る上ではあまり役に >立ちません．

しかし，実際に電磁気学の専門書や入試問題等で「→」がよく用いられており，電気力線と同じぐらいの有益性はあるのではないのでしょうか？また，このスレの議論は，電場や磁場を概念的に捕らえる手法についてなので，矢印でも電気力線でも，それほど拘る必要は無いと思いますが．(^_^;)

Re: 無題

MXK さんのレス (2007/01/07(Sun) 11:37)

質問者を放っておいてはいけませんね．

(1) 2つ以上の点電荷のつくる場は保存場ですが，中心力場にはなりません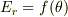． $E_r= f(\theta)$ は中心力場ですが，一般的に保存場にはなりません．

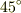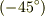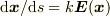(2) 原点に向かう電気力線は原点付近でモタモタした挙句，微小なズレが拡大されて結局は $45^\circ$ 方向か $(-45^\circ)$ 方向に沿って無限遠に向かうことになります．(45度ずれていました．訂正しました．) 電気力線は積分曲線として定義されているので，実際に微分方程式 ${\rm d}\bm{x}/{\rm d}s = k \bm{E}(\bm{x})$ を(数値的にでも)積分してみれば様子がよく分かるでしょう．前野先生のページに電気力線を描く話題が出ていました．

http://homepage3.nifty.com/iromono/diary/200608B.html

厳密には「電荷と電場が外に対してした仕事」なのでしょうね．

済みません，（２）を間違えました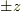． $\pm z$ 軸方向に逃げてゆくのでした．

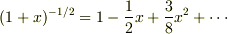$(1+x)^{-1/2}=1-\frac{1}{2}x+\frac{3}{8}x^2+\cdots$ を用いて原点付近のポテンシャルと電場はそれぞれ

$\phi=\frac{q}{4\pi\epsilon_0 a^3}[4a^2+x^2+y^2-2z^2]$

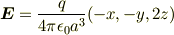
$\bm{E}=\frac{q}{4\pi\epsilon_0 a^3}(-x, -y, 2z)$

Re: 無題

yama さんのレス (2007/01/07(Sun) 12:15)

(2) きちんと計算はしていませんが，(a,0)から原点付近にに向かう電気力線がちょうどｘ軸上ではなく，ｙ軸の正の向きにわずかにずれている場合は，原点付近で向きを変えて，ほぼ直線 x=y に沿って無限遠に向かうと思います．（訂正：これは間違っていたようです．下記のミュフ猫さんが正しいと思います．）ちょうどｘ軸上を原点に向かう場合は，原点で途切れると考えても，向きを変えて直線 x=y または x=-y に沿って無限遠に向かうと考えてもいいと思います．

(2) 電場と電荷だけしか存在しない場合は，外に対して仕事はせず，電場が電荷に対して仕事をして，電荷の運動エネルギーが変化することになります．従って，一般には「電場がする仕事」というのが適切だと思います．

Re: 無題

ミュフ猫さんのレス (2007/01/07(Sun) 13:03)

yamaさんへ

>(2) きちんと計算はしていませんが，(a,0)から原点付近にに向かう電気力線が >ちょうどｘ軸上ではなく，ｙ軸の正の向きにわずかにずれている場合は， >原点付近で向きを変えて，ほぼ直線x=y に沿って無限遠に向かうと思います． >ちょうどｘ軸上を原点に向かう場合は，原点で途切れると考えても， >向きを変えて直線 x=y または x=-y に沿って無限遠に向かうと考えても >いいと思います．

私の考えでは，原点近傍は盆地のくぼみができてエネルギーの低い電荷は，外側に抜け出せないように思います．ですから，原点近傍の電気力線は原点に向かって延びて行き，原点だけ特異点となるように思います．原点近傍以外では，仰られるように，直線x=y またはx=-yに漸近する電気力線と，直線x=ky(kは1または-1以外の実数．)に漸近する電気力線とができるように思います．

Re: 無題

yama さんのレス (2007/01/07(Sun) 13:12)

>私の考えでは，原点近傍は盆地のくぼみができてエネルギーの低い電荷は，外側に抜け出せないように思います．

一般に静電場に安定な釣り合いの点（ポテンシャルの極小点）は存在しません．原点は不安定な釣り合いの点だと思います．

Re: 無題

ミュフ猫さんのレス (2007/01/07(Sun) 13:48)

yamaさんへ

>一般に静電場に安定な釣り合いの点（ポテンシャルの極小点）は存在しません． >原点は不安定な釣り合いの点だと思います．

例えば，正電荷に対しては，不安定な釣り合いの点であっても，負電荷に対しては，安定な釣り合いの点です．今，二つの正電荷だけを考えます．すると，電気力線には二点の垂直二等分線を漸近するものがありますが，その接線は必ず垂直二等分線に交わります．ということは，垂直二等分線の近傍では常に，垂直二等分線に近づけようとする静電気力が働いているということです．従って，四つの正電荷の場合は，二つの場合の重ね合わせを考えればよいだけなので，盆地のくぼみができると思うのです．

Re: 無題

kei さんのレス (2007/01/07(Sun) 14:16)

かなり書き込みが増えているのでちょっとびっくりしています．

ミュフ猫さん，

>>力線数密度は電界の面素dSに直交する成分であることが示されます．

ということは，力線数密度の大小でわかることは，電場のある方向成分の大小に限られる訳ですよね？その情報だけで，スカスカとか想像しにくい気がするのですが．

作図するときに荒っぽいですが(力線数密度) = Ecosθのθを90°にしてやれば

(力線数密度) = E

となり，力線数密度と電界が同等になり，

(力線数密度) = (力線本数)/(力線が貫く面積)

という定義を置いたので"力線が貫く面積"を一定値にするために変形することの無い面を設定してやれば

E = (力線数密度) ∝ (力線本数)

となって電界は"固定した面"を貫く力線本数に比例することを言いたかったのですがイメージしづらいでしょうか？

また"→"を使う作図法ですが，力学系のように，測定した場所において，測定したベクトル矢印を書き込んでいく類のものとみてよろしいのでしょうか？それであっているのなら，この矢印と力線は同じものではないのでしょうか？矢印は局所的に正しいですが多少目をつむってこれらの矢印を巧いこと繋げば電気力線を近似的に表現できると思いますよ．

力線も矢印も電荷を配置した際にどの向きに力が働くかを視覚的に分かるように書いたものなのでどちらを採用するかは各々のセンスに依存しているのではないでしょうか．

りんごさん，

おっしゃる通り電場の測定は可能です．測定についてはどうこう言うつもりは無く，この文を読まれたときにこちらの意図した所とりんごさんが重点を置かれた点がずれてしまうような文を書いてしまいました．

主張したかったのは，クーロンの法則を出発点とするときに電荷の電気量が"源"となるので，電荷の配置を確定するための位置(距離と面積)，とこの電気量を測ることが出来れば電磁気に現れる物理量を書けるように構成しましょう，ということなのです．

電界が測定できるということではなく，このような基礎的な電気量や位置によって電界を書くことが出来ることを説明したかったのです．

N=∫E・dS = Q/ε0

の最右辺がQを源としている電気力線の本数(Qから放射状に伸びている)であり任意に閉曲面を選んだときにガウスの法則からEの値が決定できます．

>電気力線も電界強度もダイレクトに測定できません．高校の教育過程でいうなら計れるのは，簡単な計器で距離，面積，電気量ぐらいでしょう．ここで，電界強度を定式する際にこの３つでもって式を構築しなくてはなりません．

高校生なので…というところに重点を置いているのでなく，電界そのものに移行する前に，距離や面積，電気量も大切ですよー，と説明したかったのです．

また高校生に教える際は，学校の教科書のままでいいと思いますが，やはりクーロンの法則とガウスの法則が等価であることを示したいのであるならば，クーロンの法則を解説した後に

物理学入門コース３電磁気学?(電場と磁場)長岡洋介著岩波書店

のガウスの法則の項目を積分なしで解説すればよいと思います．

文才が無く説明に乏しかったことをお詫びします．

Re: 無題

ミュフ猫さんのレス (2007/01/07(Sun) 15:39)

keiさんへ

なるほど．納得しました．m(_ _)m

Re: 無題

りんごさんのレス (2007/01/07(Sun) 17:02)

keiさん，

意外と，近い意見を持っているようにもおもいます．

私は，電磁気学の初心者さんには；

（１）万有引力の説明の，質量，そして重力場

（２）それに対比させて，静電気の力の説明(クーロンの法則)で，電荷，そして静電場

（３）電荷や質量の球殻での直接積分で，静電気に関するガウスの積分法則を誘導

がいいように思えてきました．だいたい素材はそろっているので検討してみます．

>物理学入門コース３電磁気学?(電場と磁場)長岡洋介著岩波書店

ご紹介，ありがとうございます．残念なことに，昔あることがあって，岩波の物理の本とは相性が悪くほとんど読んでいません．でも，一度，拝見しようと思います．

＝＝＝＝＝＝

yamaさん，MXKさん，

これまで戴いたご意見と，「電磁気学を考える」とを読ませていただいています．

その結果，電束管のアイデアは理解できましたが，「理論電磁気学」で育った私には，判るけど，なんで回り道な考え方をするのだろうというのが正直なところです．

＃言うなら，電場とスカラー・ポテンシャルをイメージしつつ，マクスウェル方程式の微分表現，積分表現を自在に使えれば，「電磁気学を考える」の世界も結構再現できるように思えてきましたが，まだ不勉強の身です．

ただ，このままでは，スレッドを立てられた「けん（大学1年）さんの質問」との乖離が大きすぎるとおもうので，自分なりの勉強が済んでから別途，質問とさせて戴きます．

Re: 無題

yama さんのレス (2007/01/07(Sun) 17:05)

ミュフ猫さんへ

>例えば，正電荷に対しては，不安定な釣り合いの点であっても，負電荷に対しては，安定な釣り合いの点です．

そういう可能性も考えられますね．しかし，静電場ではポテンシャルの極小点だけでなく極大点も存在しないので，負電荷に対しても安定な釣り合いの点は存在しません．

と言いたいところですが，よく考えるとちょっと問題がありました．３次元の場合はいいのですが，２次元に制限されている場合は検討が必要です．たとえばｚ軸方向の変位に対しては不安定でもｘｙ平面に制限すれば安定かもしれません．そこで，ｘ軸上の２つの正電荷を考えて，それによるポテンシャルのｘ軸上の変化を調べると原点で極小になることが分かります．しかし，ポテンシャルのｙ軸上の変化を調べると原点では極大になります．従って原点は極大でも極小でもなく，鞍点であると考えられます．これにｙ軸上の２つの正電荷によるポテンシャルを加えるとどうなるかはさらに検討を要します．しかし簡単に考えると，ポテンシャルが原点で極値をとるならば，原点近傍の電気力線はすべて原点に向かうか，またはすべて原点から出たものでなければなりません．しかし，電荷が存在しない点が電気力線の始点や終点になることはないので結局原点はポテンシャルの極大点でも極小点でもなく，安定な平衡点ではないと考えられます．（訂正：これも間違いだったようです．No.13620 参照），

Re: 無題

MXK さんのレス (2007/01/07(Sun) 18:21)

りんごさん，

今井先生ほど流体とのアナロジを徹底させる必要はないと思いますが，

幾何学的に考える
D と E の役割をしっかり区別する

というところは，大変参考になると思います．たとえば，ポテンシャルは curl E = 0 を利用しているので，E の話，電気力線の数は div D = rho に関係しているので D の話という具合です．

初心者（あるいは初学者向けの本）はともかく，電磁気学を一通り学んだ立場からは，「電気力線の数というのは，電束 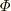$\varPhi$ のこと」という理解が必要です．

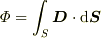
$\varPhi=\int_S \bm{D}\cdot{\rm d}\bm{S}$

Re: 無題

りんごさんのレス (2007/01/07(Sun) 18:25)

MXKさん，

>2007/01/07(Sun) 10:20 No.13539のご論議は興味深いとおもいます．

この意味で，解説を作って戴けませんか．

MXKさんのご持論を展開する上でも，「電磁気学を考える」の現代版としての解説が重要だと思います．ご検討くだされば幸いです．（希望ですので，ご回答には及びません．）

Re: 無題

ミュフ猫さんのレス (2007/01/07(Sun) 18:38)

yamaさんへ

>結局原点はポテンシャルの極大点でも極小点でもなく， >安定な平衡点ではないと考えられます．

ということは，原点に静止する電荷を無限遠点まで遠ざけるには，エネルギーを加える必要があるのでしょうか？

Re: 無題

yama さんのレス (2007/01/07(Sun) 20:38)

電荷の符号によって違うと思います．４個の電荷が正電荷で，原点に正電荷が静止しているとします．原点の電荷にわずかなエネルギーを与えれば，原点からずれて，ポテンシャルの減少する向きに無限遠に向かいます．具体的には，直線 x=y または x=-y に沿って無限遠に向かうことになるでしょう．（訂正：これも間違いだったようです．）原点に負電荷がある場合は，わずかなエネルギーを与えるとポテンシャルの増加する向きに動きます．具体的には座標軸に沿って４個の正電荷のどれかに向かって移動して衝突するでしょう．従って無限遠まで遠ざけるにはエネルギーを加える必要があるでしょう．

Re: 無題

kei さんのレス (2007/01/07(Sun) 21:32)

ミュフ猫さん，理解していただけて安心しました(^o^)/

りんごさん，詮索することはよくないこととは思いますが，おそらく熱心に高校生への教授法を書かれている点から，高校か予備校のようなところで物理を教えておられる先生だと思います．高校生に物理を教えるという状況の下での話をちょこっとさせてもらいます．

>私は，電磁気学の初心者さんには；

（１）万有引力の説明の，質量，そして重力場（２）それに対比させて，静電気の力の説明(クーロンの法則)で，電荷，そして静電場（３）電荷や質量の球殻での直接積分で，静電気に関するガウスの積分法則を誘導

がいいように思えてきました．

私もりんごさんの講義の組み方で十分に電磁気の世界への入門を解説できると思います．しかし，それは大学に入ってから初めて習う電磁気学で有効だと思うのです．

上で偉そうなことを長々と書き連ねましたが，今を去ること3,4年前私がまだ高校生だったころ，私自身それほど物理の教科は得意じゃありませんでした．むしろ苦手であったでしょう．授業では新しい物理量を記述する式が(大学ほどではないですが)怒涛のごとく紹介され，新しい考え方を図示されノートに取るのも大変であまりいい思い出がありません．

血の滲むような努力をしなかったことも大きな原因ですが，今になって振り返ると

先生は先の展開を見越しているが，私は何が目的でこのことを考えるのかが分からない

状態に陥っていたのだと思います．当然りんごさんは全て先を見越せる立場にいます．広く物理学を見渡す上で式の同等性は大きな効力を発揮しますが，それは物理を専門に扱わねばならない時に考えればよいのであって，物理チンプンカンプンの生徒に話しても左から右に抜けていってしまいます．なので

>（１）万有引力の説明の，質量，そして重力場

の項目は飛ばしたほうがよいと思います．出来るなら電磁気学の中だけで話を完結できたほうが苦手な生徒にはよいのではないでしょうか？

そこで万有引力の代わりに次のようにしてみてはいかがでしょうか？

（１）磁石にはN極とS極がある →磁気の簡単な解説 →磁荷に対するクーロンの法則 (逆2乗比例の経験的な解説，ここでは磁界の話はしない)

（２）それに対比させて，電気には+と-がある →静電気の力の説明 →電荷に対するクーロンの法則 →静電場

（３）電荷や質量の球殻での直接積分(具体的には閉曲面表面積の掛け算)で，静電界に関するガウスの法則を誘導(高校教科書程度) →(力)=(電気量)×(電界強度) であることの説明

（４）磁荷に対しても同様に (力)=(磁荷量)×(磁界強度) となる磁界強度を考えることが出来る

（１）でおそらく誰もがやったことのある磁石を引っ付けたり，反発させたりする遊びから，かなり近づけると体で感じることができる(認知できる)力が働くことから少なくとも距離の逆数に比例することを諭します．30ｃｍくらい離しておいても動かないでしょう，といったように経験から想像できたほうが初学者にはベターでしょう．この段階で深く1/(r^2)に比例することを説明するのはかえって難しくなるので実験して補正したらこうなった程度でいいのではないでしょうか．

後はりんごさんのプランの通りで，最後に似たような手順で磁界についても定式していけます，と簡単に静磁界についてかじるのが知識を増やすという意味でよいでしょう．

あと課題は難しい計算(主に微積)を使わずにどこまで微積の説明が出来るかだとおもいます．

実はバイトで高校数学を塾で教えているのですが，割と簡単な計算で詰まってしまう高校生がいます．計算といっても微積などで無く中学校でやるような文字式を簡略化していくプロセスが出来ていない生徒さんがたくさんいます．どうやら文字が増えるとアップアップしてしまうそうです．

実際の練習問題では無理ですが，現象を説明するときは少ない物理量のシンボルで解説する必要がありそうです．

簡単に言うと定式を中心とするのでなく言葉で現象を説明してその補助で関係式(たとえば F = QE)を説明するのがよいと思います．したがってたくさん図を用意しなくてはなりません．当然このスレッドの話題である電気力線なども必要になりますが，物理苦手くんには作図が最も頭に入れやすい(むしろ頭を使う)と思うので，よいトレーニングになるでしょう．

一通り物理を学び(万有引力を理解したうえで)難関大学を受験するような生徒さんには，りんごさんのプランのほうが回りくどくなく分かりやすいと思います．

いろいろ考え方はあると思いますし，受験界のプロの方から言わせるとなんてことを言うんだともいわれてしまいそうですが，かつて，どうしょうもない落ちこぼれ高校生だった人間の経験ということで参考程度にしてください．

Re: 無題

りんごさんのレス (2007/01/07(Sun) 22:37)

keiさん，

とても明快なご意見を戴き感謝しています．今後の参考にさせていただきます．

私は「健康を概してから，体のリハビリテーションに入り，こちらのサイトを拝見しているうちに，頭のリハビリテーションまでさせて戴いている老人」です．

お若い方々の質問を拝見しているうちに，物理の問題もそうですが，背景に在るはずの数学や，解説法に疑問を持ち出しています．例えば，

（１）今回の「電気力線の数密度」の取り扱い（２）力学での「準静的な力」（３）運動積分（４）微分方程式と積分（５）ベクトル解析は高校生に不可能なのか？

など，疑問が大きい渦をなしています．そこで，いつも素晴らしい解説をされていられるyamaさんに喰い下がった訳です(笑)．

今の自分には，２つの興味が在ります；

・高校生さんに，数学をつかった解りやすい力学・電磁気学の説明法を工夫したい．・大学中学年さんに向けて，洗練された数学に基づいて，ショート・カットに，真空における電磁気学の講義ノートを書きたい．

その意味では，このスレッドを立てられたけん（大学1年）さん，書かれた皆さんに感謝の意を表します．

Re: 無題

kei さんのレス (2007/01/07(Sun) 23:42)

りんごさん，確かにこれだけ有意義な議論が出来たのは，けんさんのおかげですね．はじめは唯の問題回答スレだったのに，深く掘り下げたりんごさんは老人ではないですよ．正直私が10年，20年後に同じ事を聞かれて答えることが出来るかと考えれば(笑)

昔では，たとえば物理のこの電磁気の教科書ならばジャクソンの教科書のように難しそうな本しかなかったので，やさしい本がたくさんある現代に生まれた私はありがたい時代に入るのだなぁとたまに思うことがあります．

>・高校生さんに，数学をつかった解りやすい力学・電磁気学の説明法を工夫したい．・大学中学年さんに向けて，洗練された数学に基づいて，ショート・カットに，真空における電磁気学の講義ノートを書きたい．

ご存知かもしれませんが簡単なベクトル解析を利用した電磁気の本を紹介します．

高校生向け：理系なら知っておきたい物理の基本ノート[電磁気編] 為近和彦著中経出版かなり簡単に書かれています．しかし簡単に書かれすぎて分からないところも少なからずありました．

高校〜大学生向け(主に大学生)：単位が取れる電磁気ノート橋本淳一郎著講談社サイエンティフィックこれは大学生協のロングセラーのシリーズのうちの1冊で，大学入試の参考書を書いている人気予備校講師が書いたものです．上の本も予備校講師が書いたものなので程度は同じなのですが，さすがは講談社，図がかなり見やすいです．

数学の入門書：道具としての〜シリーズ日本実業出版社もし数学で詰まっている人がいるならかなりお勧めです．このシリーズの微分方程式の本が今の私を形づくったといっても過言ではない(笑)微分方程式は大学入学が決まって大学生活が始まるまでに読みきれたので高校生でも読めると思います．電磁気に関連するのは物理数学の本のベクトル解析のしょうですかね？

初学者に教えるといった視点から見ればこういった本がいいと思います．

> MXKさん，

2007/01/07(Sun) 10:20 No.13539のご論議は興味深いとおもいます．

この意味で，解説を作って戴けませんか．

MXKさんに代わって回答になりうる図書を紹介させていただきます．ここに解説を打つのは少し荷が重いので(笑)りんごさんへの推薦と書という意味で

新版電磁気学上，下パノフスキー・フィリップス著吉岡書店上：Maxwell方程式，電磁波，電磁流体下：特殊相対性理論(Hamilton形式)，輻射，散乱，分散

上巻の4章に答えとなる解説(電界と等電位面のメッシュ)が載っています．ただこの本は現在は受注生産なので本屋さんで見かけることはまずないです．おそらくジャクソンの教科書と同じくらい世界で有名な本だろうと思います．1冊4000円近くしますので買うにしてもまずお近くの図書館(大学付属図書館や国立図書館)でまず要るところだけ見てからのほうがよいだろうと思います．ただ最近書かれた電磁気の本に比べ比較的難しい概念，数学，計算をやってのけなくてはならないので理解するには骨が折れてしまいます．

なんだかこの勢いで行ったら電磁気のトピックだけで大きなサイトが出来てしまいそうですね．

Re: 無題

けん（大学1年）さんのレス (2007/01/09(Tue) 14:51)

みなさん，ありがとうございます．書き込みが遅くなってすみません．難しい話もあって，よく分からないところもあったのですが，大変参考になりました．

(2),(5)は結論はどうなるのでしょうか？

また，(4)は，yamaさんから，

Ep の式の右辺にマイナスの符号がついているためです．これがプラスだったらポテンシャルが増加する向きになります．

という御回答を頂きましたが，マイナスだったら減少の向き，プラスだったら増加の向きというのは当たり前のことなんでしょうか？いまいちよく分からないのですが…．

よろしければ，回答の方，よろしくお願いします．

Re: 無題

ミュフ猫さんのレス (2007/01/09(Tue) 16:03)

けん（大学1年）さんへ

>(2),(5)は結論はどうなるのでしょうか？

(5)はよくわかりませんが，(2)について私の考えを述べます．この場合，原点近傍では，井戸型ポテンシャルが形成されると思います．つまり，原点では安定な釣り合いとなると思います．もし，傾き45°の方向に電気力線が流れるのであれば，少なくとも，直線 y=x上にある点のうち，原点におけるポテンシャルが最も高くなければなりません．今，点(x,y)におけるポテンシャルを φ(x,y)とすると，原点におけるポテンシャルφ(0,0)は， (4πε)*φ(0,0)= 4*(q/a) です．ところが，点(a/2,a/2)におけるポテンシャルφ(a/2,a/2)は， (4πε)*φ(a/2,a/2)= (2√2)*(q/a) +(2√2/√5)*(q/a)= (2√2)*(1+1/√5)*(q/a) (4πε)*φ(a/2,a/2)≒ 4.09*(q/a) ですから， φ(0,0)<φ(a/2,a/2) となり，点(a/2,a/2)におけるポテンシャルの方が高くなってしまいます．従って，原点近傍では，傾き45°の方向に電気力線は流れないと思います．

Re: 無題

ｙama さんのレス (2007/01/09(Tue) 16:15)

(4)について説明します． Ep は法線方向の電場の成分です．法線は正の向きと負の向きを区別するものとします．正の向きに測るときsは正です．正の向きにポテンシャルが増加する場合は dφ/ds>0 なので，Ep=-dφ/ds<0 となります．つまり電場の成分が負ということになるので，電場は負の向きをもちます．これはポテンシャルが減少する向きです．負の向きにポテンシャルが増加する場合は dφ/ds<0 なので，Ep=-dφ/ds>0 となります．つまり電場の成分が正ということになるので，電場は正の向きをもちます．これはポテンシャルが減少する向きです．

Re: 無題

けん（大学1年）さんのレス (2007/01/09(Tue) 16:29)

ミュフ猫さん，yamaさん，ありがとうございます．

Re: 無題

ｙama さんのレス (2007/01/09(Tue) 18:05)

ミュフ猫さん，貴重なご意見ありがとうございます．

ミュフ猫さんのご意見をもとに考え直してみたところ，確かにミュフ猫さんがおっしゃる通りxy平面に限れば，原点は安定な平衡点になるようです．また，原点近傍の電気力線は原点に集まることになります．

はじめは，電荷がないところに電気力線が集まるのはおかしいと考えましたが，よく考えてみると原点に集まる電気力線の本数は0本になるので問題なさそうです．というのは，電気力線の本数は，その密度が電場の強さに比例するように決めるので，ある面を通る電気力線の数はその面積に比例します．ところがxy平面は厚さが0なので，その断面積は0です．従ってxy平面内に電気力線が存在したとしても，本数としては0本です．実際は電気力線はxy平面に限定されず，全空間に広がっています．１つの電荷から原点付近に向かう電気力線がわずかにxy平面からずれている場合は，その電気力線は原点付近で向きを買えてほほz軸にそって無限遠に向かいます．従って全空間を考えても原点に集まる電気力線は0本です．

また，xy平面に制限せず，空間全体で運動できる場合は，原点は不安定な平衡点になります．たとえば4個の電荷が正電荷の場合は，原点に正電荷を置いたとき，xy平面からわずかにずれただけで，z軸方向の力を受けて無限遠に向かいます．

なお，(2)の答としては，原点に向かう電気力線は原点で途切れると考えるのが妥当だと思います．この場合，原点に向かう電気力線の本数は0本です．

Re: 無題

ミュフ猫さんのレス (2007/01/09(Tue) 23:46)

>また，xy平面に制限せず，空間全体で運動できる場合は， >原点は不安定な平衡点になります． >たとえば4個の電荷が正電荷の場合は，原点に正電荷を置いたとき， >xy平面からわずかにずれただけで，z軸方向の力を受けて無限遠に向かいます．

なるほど．三次元の場合は，電荷のない場所が安定な平衡点になることは無いということですね．勉強になります．返信ありがとうございました．m(_ _)m

Re: 無題

MXK さんのレス (2007/01/11(Thu) 16:37)

No. 13542の(2)の答えが間違っていたので訂正しておきました．

Re: 無題

けん（大学1年）さんのレス (2007/01/18(Thu) 17:01)

みなさまたくさんレスして下さり，ありがとうございました．とても勉強になりました．

[home] [掲示板] [ページの先頭]