電束は数えられるか
電束は数えられるか
篠原 さんの書込 (2006/09/02(Sat) 00:42)
物理のかぎしっぽ,メンバーの篠原です.
現在,私の記事「ガウスの法則-積分形」を査読提出中なのですが,この記事の査読において,査読者と私との間で「電束は数えられるものなのか」という事について議論になりました.
元のページ:
メンバーだけでなく,一般の方も是非議論に加わってください. よろしくお願いいたします.
Re: 電束は数えられるか
篠原 さんのレス (2006/09/02(Sat) 00:49)
私の意見を書きます.
積分形のガウスの法則において,閉曲面から出てくる電束 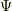 は次式で与えられます.
は次式で与えられます.
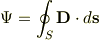
電束密度を面積分しているわけですから,電束 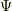 の単位は明らかに[C]です.[本]ではありません.
このため,電束は1本,2本,と数えられないとするのが私の立場です.
の単位は明らかに[C]です.[本]ではありません.
このため,電束は1本,2本,と数えられないとするのが私の立場です.
Re: 電束は数えられるか
Joh さんのレス (2006/09/02(Sat) 00:55)
ええ,元のページでは,私はろくに調べず見当はずれなことを言っていますので,お恥ずかしい限りです.
電束線っていうのは,要するに電場の流束線ですね.篠原さんの書かれた定義式は,『全流量は,湧き出しの総量に等しい』と読めます.
例えば,1単位の湧き出し(電荷)につき,電束は1本,というように,単位を決めれば形式的に数えられるんじゃないでしょうか.もちろん,実際,シマシマに電束線が見えるものではないと思いますけど.
Re: 電束は数えられるか
NOBU さんのレス (2006/09/02(Sat) 01:05)
>Johさん, 「電束線っていうのは,要するに電場の流束線ですね」 電場の流束線は電気力線というもので,実は少々違います.この違いを説明しようとすると少しややこしくなるのでここではしません.ただそれ以外はJohさんの認識であっていると思います.
Re: 電束は数えられるか
黒子 さんのレス (2006/09/02(Sat) 01:06)
私も,電束線というものが物理的に数えられるものではないと思います.
確かに,数学的(形式的)には数えられるものでしょう. しかし,それは形式的な話であって, 物理的に,電束線が数えられる実体であるかということが,電磁気をやっててずっと疑問でした.
形式的に数えられるとみなせることが,ガウスの法則の本質にせまっていることは理解できます. しかし,電束線が数えられることとは,また別な問題だと思っています.
Re: 電束は数えられるか
篠原 さんのレス (2006/09/02(Sat) 01:08)
Johさん,投稿ありがとうございます.
『全流量は,湧き出しの総量に等しい』というより,『湧き出しの総量を 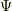 とする』といったところでしょうか・・・.
とする』といったところでしょうか・・・.
「1単位の湧き出し(電荷)につき,電束は1本」
つまり,1C=1本とおくのですか・・・?おかしくはないですか?
例えば, 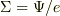 (e:素電荷)と
(e:素電荷)と 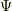 に対して
に対して 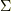 という無次元量化した新しい量を定義して,これを1本,2本と数えるのなら,納得できます.
しかし,
という無次元量化した新しい量を定義して,これを1本,2本と数えるのなら,納得できます.
しかし, 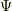 それ自身を,1本,2本と数えるのはおかしいと思います.
あくまでも
それ自身を,1本,2本と数えるのはおかしいと思います.
あくまでも 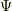 は,1C,2Cと電荷の単位を持った量です.
は,1C,2Cと電荷の単位を持った量です.
Re: 電束は数えられるか
Joh さんのレス (2006/09/02(Sat) 01:13)
>NOBUさん,
ありがとうございます (>_<) 私の電磁気学は,もう玉砕状態です.物理のかぎしっぽで, 一から勉強しようと思います (^o^)/
本当に,もし電場が見えるメガネか何かかけたら,一本二本って数えられるものではないと思います.そういう物理的実体として,整数本の線があるとは思いません.前の書き込みの繰り返しになりますが,単位電荷当たり何本と決めれば,数えられるとしていいのではないか,と思うのですが.少し議論が違う方向へ行っている気がします.
黒子さん> ガウスの積分法則は,全体での総流量と湧き出し量が分かればいいので,流束密度(?)が整数本で数えられるかどうか,と言う点は本質的ではないと思います.
Re: 電束は数えられるか
Joh さんのレス (2006/09/02(Sat) 01:18)
>篠原さん,
そんな,次元の違う量をイコールで結ぶつもりはありませんよ.(一人当たりのお弁当代が1000円だとして,人=円ではありませんよね.)問題ありますかねぇ.
それ以上のことは,私は電磁気学の門外漢ですので,静かに議論を傍観させていただいて勉強しようと思います.(^_^)/~
Re: 電束は数えられるか
NOBU さんのレス (2006/09/02(Sat) 01:26)
篠原さん> 篠原さんの「ψそれ自身を,1本,2本と数えるのはおかしいと思います.」 この認識はあっていると思います. ただ,電束線自体は地図の等高線と同じようにイメージしやすいように導入された概念だと思います.積分した量はもちろん[C]の単位を持ちますが,電束線をJohさんのおっしゃるように定義しておけば積分した値を本数に読み替えることもできますねということです. 篠原さんのおっしゃているのは,地図の等高線の密度を勾配大きさに比例して書いた時に,どうして等高線の密度[本/m]が勾配の大きさ[無次元]と一緒になるんだ,単位が違うじゃないかと言っているのと同じ気がしてしまいます.どうもその辺りに認識の違いがあるような気がします.
Re: 電束は数えられるか
篠原 さんのレス (2006/09/02(Sat) 01:26)
>Johさん, 一人当たりのお弁当代が1000円だとして,人=円ではありませんよね.
面白い例えですね. では,今5000円のお金があったとします.5人分の代金です. 「お金」という量を「人」という単位で数えたことになるのですか?
同様に,5Cの電束がわきだしているとします.1Cあたり1本と仮定します.5本分の電束です. 「電束」という量を「本」という単位で数えたことになるのでしょうか?
Re: 電束は数えられるか
Joh さんのレス (2006/09/02(Sat) 01:30)
5000[円] = 5 [人] × 1000 [円/人]
だと思いますが,篠原さんの書き込みの意味はよく分かりません.私は,見当違いなことを言っているでしょうか?
(単位に括弧は要りません.)
Re: 電束は数えられるか
MXK さんのレス (2006/09/02(Sat) 01:35)
すでに指摘されているように,電束の数は単位を決めないと意味を持たせることはできません.例えば,(Φ/C) 本のように. 単位のとり方には任意性があるので,必ず指定する必要があります. 地図上の2点間の「等高線の数」なども類似の概念です.等高線を描くときには,100m間隔 とか 25m 間隔とかを決める必要がありますが,これが単位を指定していることに相当します.また,電束の数は整数である必要はありません. グラフ用紙や定規のような,入れ子になった目盛りを想像することも有効です.
Re: 電束は数えられるか
篠原 さんのレス (2006/09/02(Sat) 01:42)
NOBUさん>
>電束線をJohさんのおっしゃるように定義しておけば
なんども質問していますが,そのような定義は一般的なのですか? そのような定義が一般的に広く「1Cの電束を1本と数える」といったことが知られているなら,記事の中で使っても良いの<b>かも</b>知れませんが,一般的に知られていないのなら,逆に混乱を招くだけです.
Johさん> 混乱させたようですみません. 私の意図が伝わらなかったようです. 意味が分からなければ,無視してください.
Re: 電束は数えられるか
Joh さんのレス (2006/09/02(Sat) 01:53)
>篠原さん,
たぶん私の理解力不足です.私にも分かるように説明して欲しいところですが,無視しろというならしょうがないです.(>_<;)
>MXKさん,
書き込みありがとうございます.非常に納得します.
Re: 電束は数えられるか
NOBU さんのレス (2006/09/02(Sat) 01:59)
篠原さん> 僕も何度も書いていますが,1Cの電束を一本と言っている訳ではありません. 電束線の密度を,(電束密度の大きさ)×(dS)の大きさに比例して描くといっています.ただしその比例定数が”1”と決まっているというのは間違いかもしれないと言いました.
たぶん篠原さんの使っている電束と僕の使っている電束線の意味が違うから誤解が生じるのでしょう.僕は篠原さんのいうところの電束の大きさに比例させて電束線の密度を描くといっています.何も電束線と電束(そもそも(電束密度の大きさ)×(dS)を電束と一般的に呼ぶのか疑問に思っていますが)を同じ次元だとは言っていません.
Re: 電束は数えられるか
NOBU さんのレス (2006/09/02(Sat) 02:03)
少し日本語が変でした. 「電束線の密度を篠原さんのいうところの電束の大きさに比例させて描く」とした方が分かりやすいですかね.
Re: 電束は数えられるか
篠原 さんのレス (2006/09/02(Sat) 02:04)
Johさん,すみません. 私の表現が悪かったのです.
> 説明して欲しいところですが
はい.説明します.
5000円は5人<b>分</b>の代金ということはできますが,5人の代金ということはできません. これは,「お金」という単位が「一人二人」と数えられる物ではないからですよね.
同様に,電束 5Cは5本<b>分</b> ということはできるかもしれませんが,電束 5本ということはできません.
数えられるものではないからです.
上であげたように,仮に 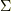 という量を考えた場合,5本でも6本でも数えてもらって結構だと思いますが,これは,電束とは全く別の次元を持った量なので,これを電束と呼ぶべきではありません.
という量を考えた場合,5本でも6本でも数えてもらって結構だと思いますが,これは,電束とは全く別の次元を持った量なので,これを電束と呼ぶべきではありません.
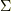 を仮に「電束力線」みたいに呼ぶとしたら,電束1C,電束力線○○本と呼ぶことはできると思いますが,電束を数えたことにはならないと思います.
を仮に「電束力線」みたいに呼ぶとしたら,電束1C,電束力線○○本と呼ぶことはできると思いますが,電束を数えたことにはならないと思います.
Re: 電束は数えられるか
篠原 さんのレス (2006/09/02(Sat) 02:12)
> NOBUさん,
>たぶん篠原さんの使っている電束と僕の使っている電束線の意味が違うから誤解が生 >じるのでしょう.僕は篠原さんのいうところの電束の大きさに比例させて電束線の密 >度を描くといっています. >何も電束線と電束(そもそも(電束密度の大きさ)×(dS)を >電束と一般的に呼ぶのか疑問に思っていますが)を同じ次元だとは言っていません.
だったら,なぜ私の書いた記事が問題なのでしょうか? 仮に電束線が本と呼べる量であったとしても,私の記事においてはすべて「電束」と書かれていて,「電束線」という表現は出てきていません. また,問題となっている注釈部分も,「電束は1本2本と数えられる量ではありません」といっているだけです. このことはNOBUさんも何度か認められたはずです.(No.11621 など)
私の記事の何が問題ですか?
Re: 電束は数えられるか
NOBU さんのレス (2006/09/02(Sat) 02:13)
篠原さん,No.11630のように認識しているのであれば,僕との議論が平行線になったのはたぶん言葉の問題から来るものでしょう.僕の言っている電束線とは11630のΣです.なので僕の使っている電束線と篠原さんの使っている電束力線は同じものです.
Re: 電束は数えられるか
NOBU さんのレス (2006/09/02(Sat) 02:25)
No.11631に対する返答です. 僕は篠原さんが電束線と{(電束密度の大きさ)×(dS):(電束)}をごっちゃにしてしまっていると考えたので指摘をしました.それが間違いであったようなのでそこはお詫びします.
ただ,そこまで理解しておられるのであれば電束を数えるという表現ではなく,電束を足し合わせるではだめでしょうか.「電束を数える」と言う表現は電束線のことを念頭に入れているからで,それなのに電束線の定義は全く書かないで,本数を考えるのはあくまで比喩的というのは初学者にやさしいとは僕には思えません.もちろん,これは個人的な意見であり,提案であるので篠原さんが違うと思えば却下してもらってかまいません.
Re: 電束は数えられるか
篠原 さんのレス (2006/09/02(Sat) 02:25)
NOBUさん,そうですか. 結局単なる言葉の問題でしたか・・・. なんだか,あっけない議論でしたね・・ :)
この「電束と電束線」の議論,どうしますか? ガウスの法則の中に,注釈か何かで触れますか?(コラムみたいなセクションを作ってもいいかも.) それとも,これだけで一つの記事にしますか?(「電束密度とは」の説明と一緒にとか.)
とりあえず,議論を掲示板からwikiに戻しましょう.
Re: 電束は数えられるか
Joh さんのレス (2006/09/02(Sat) 02:27)
>5000円は5人分の代金ということはできますが,5人の代金ということはできません.
ですから,上に書いたように,式の意味は5000[円] = 5 [人] × 1000 [円/人]で尽くしているのですが.「一人当たり」が1000円です.ですから,5000円は,「五人分」です.
私は,間違えようのない別の単位の例として,お金と人数を挙げました.ですから,最初から,お金で人数を数えようとは思ってません.MXKさんも書いているように,まず単位を決めないと議論は全て無意味だと思います.
『単位を決めれば数えられる』『単位を決めなければ数えるという行為自体無意味である』
このことに尽きるのではないでしょうか.電束という物理量を自然数で数えるのは自明ではないと思いますから(これは全員の共通認識だと思います),「単位を決めれば」と条件つきで言っているわけです.『〜あたり何本』という表現を繰り返し使っているのに,どうして篠原さんが,単位が違う,と言っているのか分かりません.単位を人間が決めちゃダメなんですか??単位って,そういうもんだと思うのですが...
ええと,そして議論は言葉の定義という方向で収束しているようですね.勉強になります (^^)
Re: 電束は数えられるか
Joh さんのレス (2006/09/02(Sat) 02:30)
は!!
私が書き込んでいるうちに,NOBUさんと篠原さんの間で議論が終結していました.では,言葉の定義が問題だったということで,議論は終了ですね ^^
パパパンパパパンパパパンパン (イヨ)
パパパンパパパンパパパンパン(ハイ)
パパパンパパパンパパパンパン
(勝手に三本締めの音頭を取らせていただきました)
Re: 電束は数えられるか
黒子 さんのレス (2006/09/02(Sat) 02:36)
結局,ずっと傍観していました.すいません..
ずっと平行線だった議論が,落ち着いてほっとしています. 言葉,定義の問題でしたか. 私も,とても勉強になりました.
Re:電束は数えられるか
tadash さんのレス (2006/09/02(Sat) 03:06)
僕が高校時代に使っていた物理?Bの教科書に次のようなことが書かれていました.
「電場の中で正電荷を電場から受ける力の向きに少しずつ動かすと,1つの線をえがく.この線に正電荷が動いた向きの矢印を付けたものを電気力線という.
電気力線は正の電荷から負の電荷に入り,また,電気力線上の各点での接線は,その点での電場の方向と一致する.
さらに,電場の強さが ![E[N/C]](http://hooktail.maxwell.jp/bbslog/94bd9eb25ecf4add3aca697951d28ccd.png) のところでは,電場の方向と垂直な断面を通る電気力線を,単位面積当たり
のところでは,電場の方向と垂直な断面を通る電気力線を,単位面積当たり  本の割合で引くものとすると,電気力線によって電場の強さも表すことができ,電場が強いところほど,電気力線が密集することになる.」
本の割合で引くものとすると,電気力線によって電場の強さも表すことができ,電場が強いところほど,電気力線が密集することになる.」
そこで,
![Q[C]](http://hooktail.maxwell.jp/bbslog/8c6909e20337d34941210c99d5e3a69e.png) の正電荷から出る電気力線の総数を求めるのに,正電荷を中心とする半径
の正電荷から出る電気力線の総数を求めるのに,正電荷を中心とする半径 ![r[m]](http://hooktail.maxwell.jp/bbslog/7a2674e9075bafcfebdc964e023576d3.png) の球面を考え,この球面上では,電場の強さは
の球面を考え,この球面上では,電場の強さは ![E=\frac{Q}{4\pi\epsilon_{0} r^2}[N/C]](http://hooktail.maxwell.jp/bbslog/823342220a64d4abb9ea658a7d780f7a.png) であり,この球面を貫く電気力線の総数は,
であり,この球面を貫く電気力線の総数は,
![4\pi r^2 [m^2]\times E [](http://hooktail.maxwell.jp/bbslog/a4d9752c34f2e771fc109dfb16c72acc.png) 本
本 ![/m^2]= \frac{Q}{\epsilon_{0}}[](http://hooktail.maxwell.jp/bbslog/07270cb488ab2e88ef399130a5b139f9.png) 本
本 ![]](http://hooktail.maxwell.jp/bbslog/0fbd1776e1ad22c59a7080d35c7fd4db.png) となって,
これは,ガウスの法則にほかならないと思います.
さらに電場と電束密度には
となって,
これは,ガウスの法則にほかならないと思います.
さらに電場と電束密度には 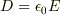 という関係が成り立ってますし・・・,
という関係が成り立ってますし・・・, ![[N/C]=[](http://hooktail.maxwell.jp/bbslog/1a8e92a0862f99af89f56b074fbb0e89.png) 本
本 ![/m^2]](http://hooktail.maxwell.jp/bbslog/0f93035250c7f82ec06b722f41c4c5ae.png) の関係もわかりますよね.このことから,電気力線,電場,電束密度の関係がわかると思います.
そこらへんも考慮してみてはいかがかと・・・
の関係もわかりますよね.このことから,電気力線,電場,電束密度の関係がわかると思います.
そこらへんも考慮してみてはいかがかと・・・
Re:電束は数えられるか
篠原 さんのレス (2006/09/02(Sat) 14:11)
議論は収束しましたが,しつこいようですが何点か気になる点があるので投稿します.
>Johさん, 私の書き方が悪いようで,なかなか私の意図が伝わりませんね... すみません.
>『〜あたり何本』という表現を繰り返し使っているのに,どうして篠原さんが,単位が違う,と言っているのか分かりません. > 単位を人間が決めちゃダメなんですか??単位って,そういうもんだと思うのですが...
今の場合,私は「電束は○○本と数えることはできない」といっているのです. 単位は単位系と物理量が決まれば,決まります. 単位系:SI 物理量:距離 と決まれば,単位:メートル と決まりますよね..(SI接頭語も含みますが.) すでに単位が決まっている物理量に対して,新たな単位を好き勝手に付けることはできません. 今の場合,電束線[本]=電束[C] ÷ 定数[C/本] という<b>換算</b>を行うことはできますが,これは電束[C]を1本2本と数えているのではなく,電束線を1本2本と数えているわけです. 今の場合,電束線と電束は全く違った単位を持った全く別の物理量です.電束線が1本2本と数えられるからといって,電束が1本2本と数えられる訳ではありません.
また,単位を決めるということは,逆にどのような物理量を測定するか,ということを決めることと等価だと思います. 単位が違えば測定する物理量も違います. 電束といった場合,単位は[C]なので,単位[本]を使うには全く別の物理量を考える必要があると思います.
「単位が違う」と言っていた意味,ご理解いただけたでしょうか?
今回の議論では,NOBUさんの「電束線」という表現と,私の「電束」という表現がお互いに同じものだと誤解しあって平行線になってしまったと思います. 議論を始める前に,お互いが使う言葉の定義を確認するべきでしたね... 反省します.. :(
> tadashさん,
[N/C]=[本/m^2]という関係,明らかにおかしいと私は思うのですが. 議論が後戻りするので,長々とは書きませんが.
Re:電束は数えられるか
篠原 さんのレス (2006/09/02(Sat) 15:13)
>こんなことは,もっと手短に説明できますね...
すみません.説明が下手で・・・. :( 私も,電束線と電束の違いに気づいたのがかなり後だったもので.. 私の反省点です :(
でも,いいわけですが, お互いが言葉の定義について誤解しあった状態で,もっと手短に説明するの,難しくないですか・・・? NOBUさんは私の電束を電束線と誤解していたわけですし,私はNOBUさんの電束線を電束と誤解していたわけで,,, お互いがいくら正しいことを言っても,相手には間違っていることを言っているようにしか思えないのでは・・・?
Re:電束は数えられるか
MXK さんのレス (2006/09/02(Sat) 15:40)
篠原さん,
これはSI単位系ということを忘れた方がいい場面です.
単位は量を(数として)測るための基準量にすぎず,その選択には
任意性があります.
地図の等高線とのアナロジをよく考えてみてください.
2地点間に等高線が 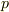 本通っていた場合,
標高差を
本通っていた場合,
標高差を 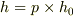 と求める
ことができます.ここで
と求める
ことができます.ここで 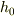 は等高線1本あたりの
標高差で,これが「単位」の役割をしています.
地図によって
は等高線1本あたりの
標高差で,これが「単位」の役割をしています.
地図によって 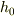 は自由に選ばれています.
これをSIを用いて
は自由に選ばれています.
これをSIを用いて 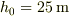 と
表すこともできます.
と
表すこともできます.
電束は「線」ではなく「管」の集まりと見るのが適当なのですが, 深入りしないことにしましょう.
Re:電束は数えられるか
篠原 さんのレス (2006/09/02(Sat) 16:15)
MXKさん,
大変申し訳ありませんが,よく分かりません.
> これはSI単位系ということを忘れた方がいい場面です.
SIでなくとも,cgsでも,どんな単位系でも良いとは思いますが・・・.
例えば,SIでは,
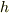 [m]=
[m]= 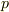 [本]
[本] 
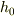 [m/本]
ではないのですか?
もちろん,[本]は無次元量なので,
[m/本]
ではないのですか?
もちろん,[本]は無次元量なので,
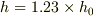 と書くことはできますが,
と書くことはできますが,
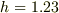 と書くことはできないはずです.「
と書くことはできないはずです.「 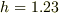 本 」という書き方も同様です.
私は,電束
本 」という書き方も同様です.
私は,電束 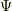 が,
が,
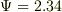 本と書くことはできない,と述べているつもりなのですが,,,
どこか変ですか・・・?
本と書くことはできない,と述べているつもりなのですが,,,
どこか変ですか・・・?
> 電束は「線」ではなく「管」の集まりと見るのが適当なのですが,
この点は納得できます. そもそも「電束線」という呼び方は,個人的にはあまり使いたくないのですが,一般的に使われているようなので・・・.
Re:電束は数えられるか
CO さんのレス (2006/09/02(Sat) 16:35)
CO です.
参考のために「電束」と「電束線」を 物理小事典 第四版 (三省堂) から引用しておきます.
<b>電束</b> 電界中に一つの面を考え,この面の法線方向の電束密度の成分をこの面について積分したものを電束という.ある閉局面を通って出る電束は,その内部の真電荷の総量に等しい(SI単位).1つの電束管についてみれば,どの断面でも電束は同じである.電束のSI単位はクーロン(C)である.
<b>電束線</b> 電界の中に曲線を考え,その曲線の接線がその場所の電束密度に平行の時,この曲線を電束線という.閉じた曲線と交わる電束線で囲まれた管を電束管という.電束線は正の真電荷から出発し,負の真電荷で終わる.真電荷がなければ,電束線は閉じた曲線になる.
(おまけ) <b>電気力線</b> 電界内に電界の方向を接線とするような曲線を考えたとき,これを電気力線という.ある閉曲線を通る電気力線で囲まれた部分を電気力管という.真空や等方性物質では電気力線は電束線と一致することが多いが,結晶では一致しないのが普通である.
Re:電束は数えられるか
MXK さんのレス (2006/09/02(Sat) 18:17)
篠原さん,
だいたい認識は一致しているのですが,少し気になるところが 残ります.
「電束線と電束は全く違った単位を持った全く別の物理量です. 電束線が1本2本と数えられるからといって,電束が1本2本と数えられる 訳ではありません.」
といわれる辺りです.
物理量 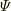 を単位
を単位 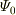 を
用いて
を
用いて 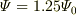 と表すときの数
1.25 は単位の選び方に依存するので物理量とはいえません.
むしろ,物理量の「表現」というべきものです.
電束管はこの数の図的な表現です(1.25本の電束管).
と表すときの数
1.25 は単位の選び方に依存するので物理量とはいえません.
むしろ,物理量の「表現」というべきものです.
電束管はこの数の図的な表現です(1.25本の電束管).
(電束) = (電束管の数) × (電束の単位)
電束管(線)は電束を計量する手段と位置づけるのが適当だと考えます.
Re:電束は数えられるか
toorisugari no Hiro さんのレス (2006/09/02(Sat) 19:10)
ああ,おもしろいスレッドに乗り遅れてしまいました.(T_T) もう収束したようなので,蛇足な話として無視してください.
私は電束は概念上は本数で数えられると考える主義者です(MXKさんのお考えに近いと思います).ただこれは「作図」上の便宜といってもいいわけで,電束そのものが数えられるというより,計量の仕方が本数で数えるタイプのグループに属してるという感じです.
(体積)密度量を作図するとき,濃淡で表現する以外に,点の粗密で表現する方法があります.たとえば,連続な電荷密度を点で表現することを考えます.ある体積に含まれる量をある単位で割ってできる「整数化した商」を元に点を打っていくと作図できます.
これは連続分布を離散分布で表現していることになるので,正しいものではないですが,「体積」と「単位」を十分小さくとれば作図法として悪いものではないですね.
ある領域の電荷はそこに含まれる点の「個数」で表せる訳です.もちろん,これは便宜上の考え方にすぎず物理的実体とは関係ない話です.(確かに電荷には最小単位はありますが,単に偶然というだけです.)
(体積)密度量のほかに双対ベクトル(gradient)を「枚数」で数えるという考え方もありますね.
実はこれらは体積密度,面密度ベクトル,線密度ベクトルに分類される量です.
作図法あるいはイメージの手段として,「密度量の積分」を個数,本数,枚数と数えるのは悪くない考え方だと思います.ただ,それは物理的実体がcountableと言う意味ではなく,ある幾何学構造(あるいは計量法)のグループに属してるというだけです.(9/4 追加:これは結局,あるスカラー量が点,線素,面素,体積素のどれの上で定義されているか,の区別ということになります.)
Re:電束は数えられるか
MXK さんのレス (2006/09/02(Sat) 21:18)
はい. 数学的に見ても,かなり必然性のある表現方法だと思います. 点分布,管束,平行面群はそれぞれ,3形式,2形式,1形式(双対ベクトル)の 幾何学的表現に他なりません. 体積積分,面積積分,線積分は個数,本数,枚数を累計する操作です.
Re:電束は数えられるか
NOBU さんのレス (2006/09/02(Sat) 21:24)
MXKさん,toorisugari no Hiroさん お二人の説明でかなり認識が深まりました. 分かりやすい説明をして頂きどうもありがとうございました.
Re:電束は数えられるか
Joh さんのレス (2006/09/02(Sat) 23:16)
MXKさん,toorisugari no Hiroさん
なるほど.何となく,そんなことを感じていたのですが, うまく言葉になりませんでした.とてもすっきりした説明を ありがとうございました!
Re:電束は数えられるか
toorisugari no Hiro さんのレス (2006/09/04(Mon) 16:17)
さらに蛇足です.
ベクトルは長さ(あるいは面積ベクトルなら長さの2乗)で計量されるものだけでなく,1/長さ(あるいは1/長さの2乗)で計量されるものがあり,そういう考えの基で作図をすると今までのベクトル解析の見方がガラッと変わります.
もし,上の考え方に興味を持たれたのでしたら, 一度ご紹介しましたが, "Geometrical Vectors" Gabriel Weinreich
をお読みになるとおもしろいと思います. (英語ですが,読み易いです.安いし.)
Re:電束は数えられるか
toorisugari no Hiro さんのレス (2006/09/04(Mon) 17:02)
MXKさん,followありがとうございます.
> 点分布,管束,平行面群はそれぞれ,3形式,2形式,1形式(双対ベクトル)の幾何学的表現に他なりません.
ちょっとだけ訂正すれば,「3形式,2形式,1形式における共変(双対)テンソル部分の幾何学的表現」ですよね.
Re:電束は数えられるか
MXK さんのレス (2006/09/04(Mon) 23:30)
toorisugari no Hiro さん,
普通,p形式は反対称p階共変テンソル場のことなので冗長ではありませんか? お勧めの本はぜひ読んでみたいと思います.
篠原さんの原稿は改訂されたようですが, 「電束線って物理量なの?」という問いには違和感があります. 「等高線って物理量なの?」あるいは「線って物理量なの?」という感じです. 電束管の数が整数に限らないと書かれているのは大変いいとおもいます.
それから,ひつこいようですが,単位の[ ] が気になります. [xx] は xx の次元という意味にリザーブしておいた方がいいと思います.
Re:電束は数えられるか
toorisugari no Hiro さんのレス (2006/09/05(Tue) 10:26)
MXKさん:
> 普通,p形式は反対称p階共変テンソル場のことなので冗長ではありませんか?
書いた後でそういう可能性もあるな,と気づきました.私は「微分形式のp形式 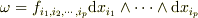 の
の  の部分」ってつもりでした.
の部分」ってつもりでした.
Re:電束は数えられるか
MXK さんのレス (2006/09/08(Fri) 20:30)
toorisugari no Hiro さま,
お勧めの "Geometrical Vectors" Gabriel Weinreich 入手しました.いい本ですね. 天下り的なベクトル解析にうんざりしている人に最適です. 強力な視点が得られます.
Re:電束は数えられるか
toorisugari no Hiro さんのレス (2006/09/08(Fri) 21:07)
MXKさま
お気に入ってもらえてうれしいです.
ところどころ?な部分(たとえば「物干し竿」解釈のところとか)もありますが,共変・反変テンソルの視覚的なイメージやガウス・ストークスの定理の驚くべき説明など,いろんな人におすすめできる本だと思います.(Hermaphrodite とか menagerieとか変な単語を使うので辞書がいりますが,絵付きなので全体としては易しいですし.)
ところでMXKさんは > 点分布,管束,平行面群はそれぞれ,3形式,2形式,1形式(双対ベクトル)の 幾何学的表現に他なりません.
という解釈をどの本で得られたのでしょうか?講義などの口頭でしょうか. もし,本があれば教えていただきたいのですが.(シュッツの「物理学における幾何学的方法」にもちょっとだけ触れてありますよね.)
Re:電束は数えられるか
MXK さんのレス (2006/09/08(Fri) 21:16)
toorisugari no Hiroさん,
微分形式の幾何学的解釈は最初
Misner et al.: Gravitation
で知りました.電話帳のように分厚い本なので誰にでも おすすめというわけには行きませんが.
その後,
Schouten: Tensor Analysis for Physicist
という,かなり凝った本にも出会いました.
Re:電束は数えられるか
toorisugari no Hiro さんのレス (2006/09/08(Fri) 22:00)
MXKさん: ありがとうございます.
「電話帳」ですか...話には聞いているのですが,さすがにきびしいなあ. あと,Schoutenは休刊みたいですね.残念.
手に入れやすそうなものとして "A First Course in General Relativity" Bernard F. Schutz
も気にしているのですが,これはどうでしょう?
Re:電束は数えられるか
MXK さんのレス (2006/09/10(Sun) 14:49)
toorisugari no Hiro さん,
「電話帳」は無理して買う価値はあると思います. Schouten は古本で入手できるかもしれませんね. Schutz の本は残念ながら見たことがありません.
肝心の電束の議論の方は迷走しているようですね.
「電束線(管)は,電束あるいは電束密度を定量的,幾何学的に表現する手段である.」
ということでいいと思うのですけれどね. 量や単位の話と同様,結構内容が深いので理解されにくいのでしょうか.
Re:電束は数えられるか
toorisugari no Hiro さんのレス (2006/09/11(Mon) 16:32)
> 「電話帳」は無理して買う価値はあると思います.
(^^) わかりました.1万8千円はつらいし,すごい厚さの英語本に恐怖は感じますが,無理して買います.
背中押してもらって感謝です.
Re:電束は数えられるか
yama さんのレス (2006/09/11(Mon) 17:25)
米Amazonから購入すれば少し安くなりそうです. 本体$100.76 送料遅い便で$8.39〜速い便で$23.39 のようです.
「Gravitation」で検索したら,日本人が書いた「Gravitation」もありました.
これを読んで重力理論がマスターできるでしょうか?
Re:電束は数えられるか
toorisugari no Hiro さんのレス (2006/09/11(Mon) 19:23)
> 「Gravitation」で検索したら,日本人が書いた「Gravitation」もありました. > http://www.amazon.com/Gravitation-Vol-1-Maki-Murakami/dp/1591823331/sr=1-1/qid=1157961948/ref=pd_bbs_1/104-7665883-7211902?ie=UTF8&s=books > これを読んで重力理論がマスターできるでしょうか?
yamaさんが冗談書いたの初めて見ました.(^^)