ゆうすけ４００ さんの書込 (2006/10/21(Sat) 14:04)

偶然通りがかっただけの者です． 塾の講師をしておりまして，高校生に基礎的な物理を教えてます． しかし，物理は大学の教養で習ったくらいであり，ひどく理解が浅いです．

電磁気学の電場と起電力について，昔から気になっていて， 解決できてないままのところがあり，そこを教えて頂きたいです． お手数ですが宜しくお願いします．

円形コイル(全抵抗R）を考え，それを貫く磁束を変化させ 電流を流す状況を考えます．

すると，キルヒホッフの第二法則から -dΦ/dt=IR という式ができます．

このときに，コイル内の電場はどうなっているのでしょうか？ そこを是非とも教えてください．

IRという電圧降下が起こっている以上， 電位が定義されており，クーロン電場も生じていると思ってます． しかし，このクーロン電場ができるためには，どこかに 電荷が溜まっている必要があるのにも関わらず， 一様な円形コイルでは， 伝導率が違ったりするような電荷が溜まりうる場所があるとは 思えないのです．そのために，そもそもクーロン電場が どうやって生じているかがわかりません．

また，磁束が変化しているので，ファラデーの電磁誘導の法則から ファラデー電場ができているとは思います．それが起電力になっている ことまでは納得している（つもり）です． しかし，そこから先の，電圧降下との絡みがさっぱりわかりません．

恐らく，どこかに根本的な誤解をしている箇所があると予測してます． しかし，そこがどこかがわからないままでいます． お手数ですがどうか宜しくお願いします．

広太 さんのレス (2006/10/21(Sat) 17:48)

この問題はぼくも疑問をもっていました． いくつかの疑問が混ざっているように思えます．

ぼくなりに一個の疑問をとりだすと 「クーロン電場と誘導電場（これをファラデー電場といっているんですよね？） が導線中にできていると思われるが， クーロン電場の源となる電荷はどこにあるのか？」 でいいですか? ぼくの理解では，クーロン電場＝０です．

そして，電位の問題ですが，静電場以外では，ポテンシャルは定義できない． ただ，起電力という概念を用いてあたかも電位が定義出来るようにみせかけて計算しているだけではないでしょうか？だから，電場をループにそって積分してゼロでなくて問題ない． 疑問を読み取れているかわかりません． また，完全な理解ではありません．ご意見お願い致します．

いち さんのレス (2006/10/21(Sat) 21:56)

あまりにもあっさりかもしれませんが，

０．磁荷があって，磁場 １．電荷があって，電場 ２．磁場が変じて，電場 ３．電場が変じて，磁場

と理解してます．

広太 さんのレス (2006/10/21(Sat) 22:21)

いちさんは， マクセル方程式のことをおっしゃっていると思います． そうであれば，そのとおりです． しかし，もとの質問には，それを解かないと意味をもたないのではないでしょうか． マクセル方程式はどれが原因でどれが結果というふうに分けられず，相互作用するのでぼくには，０から４の言葉で納得することができません． 導線内の電場について，いちさんの理解をお聞かせ頂きたいと思います．

ＺＩＧ さんのレス (2006/10/21(Sat) 22:45)

結論から言うと例えば銅線の長さｄのコイルでＶの電圧降下が起こっているとすると，Ｖ/dの大きさの電場ができています．ここで，電化が溜まっていない，あるいはポテンシャルがおかしくなる，という違和感がありますがその通りです．磁場の変化がある以上電場の保存場は定義できません． 磁場に変化が起きると，電場に渦が生じます．つまり一週回ってきたときに電位の値が変わってしいます．（V=gradEですがそれにはrotE=0必要) 例えばある円上の銅線の内部で磁場が変化していた場合この円に沿って電場が生じ，電流が流れますが，明らかにこの円上で電位を定義する事はできません．

いち さんのレス (2006/10/22(Sun) 01:03)

広太さん，みなさん

導線内は，ZIGさんと同じで，電流があらわれる以上，約一回りの電場だと思ってます（磁場を打ち消すための）． でも完全な一回りではないから，うまくこの電場の向きとは直角みたいな起電力が取り出せるんですよね． やはり，「螺旋」という形のなせる業なんでしょうね〜．

で後は，起電力の大きさですが，私も「これは１巻きコイルのｎ倍だよ」とさも分 かりきったことのように高校生に教えてます（＾＾； 「巻き方によらないの？」とか言われると正直やばい・・・

なんかポイント外してたらご指摘ください．

ゆうすけ４００ さんのレス (2006/10/22(Sun) 12:38)

皆様

様々なご教授本当にありがとうございます．

＞広太さん はい．誘導電場＝ファラデー電場のつもりです． そして，クーロン電場の源の電荷が どこにあるのかがわかっていません．

しかし，その電荷がもしも存在しないとすると， IRという電圧降下の理屈が理解できないのではないか と悩んでいます．

というのも，そもそもV=IRという式は， 電流が流れる(＝原因）から電圧降下が生じる(＝結果） という関係式ではなく， 電位差があるため(＝原因），中で電場ができ， その結果電子が力を受けてそれが電流となる(＝結果） というものであると理解しています． と，すると，円形コイルの問題で，IRとかくということは 前提として，電位差，つまり(保存力である)静電場が生じている はずなのに，そのために必要な，電荷がたまるということが 生じていないのです．そこのところを，お教えください．

＞ZIGさん コメントありがとうございます． 誘導電場について内容はまさにおっしゃっている通りだと思います． 自分がわかっていないところは，その場合のIRというものを どう処理するか，その処理の仕方です． IRというものを書いているからには，その前提にある保存場 (クーロン電場(＝静電場））があるはずと思うからです．

＞いちさん コメントありがとうございます． ちなみに起電力の大きさは巻き方にはよらないと思います． そう考える理由はまた後ほど述べさせてください．

広太 さんのレス (2006/10/22(Sun) 15:46)

このへんの疑問はぼくも持っていましたが，今は，次のように理解しています． 回路においては，電位という言葉が，拡大解釈されて使われていると思います． 電磁気学における電位（クーロン力による位置エネルギー）という言葉は， 静電場以外では成立しません．起電力がある回路では電位は定義できません． 電池のなかでは，「低電位から高電位」に流れていることになっているのです． しかし，起電力という概念を用いてあたかも，電位を定義出来るかのように扱うと，電流などの量が簡単にだせる．

だから，エネルギーではなく，直接力で考えるべきです．原因は電位差ではなく，電場です．だから ＞電位差があるため(＝原因），中で電場ができ， その結果電子が力を受けてそれが電流となる(＝結果） は，おかしいのではないでしょうか．

いかがでしょうか

ゆうすけ４００ さんのレス (2006/10/22(Sun) 16:23)

広太さん，返信ありがとうございます．

うーん，本当にそうなのでしょうか？

例えば電池に抵抗をつないだ回路を考えるとします． その回路では(電気伝導度が一様でない部分である) 電池と導線との接触部で電荷がたまります． そのたまった電荷が静電場をつくります． その結果，電位差が生じます． その電位差は(当然)一周してもとの場所に戻ると０になります．

つまり，電池なら電池内において，＋からーに向かって 静電場ができています．

起電力とは，その静電場による力に抗って， 電荷を移動させる力(正確には１Cあたりの仕事)だと理解しています． （参考：「電磁気学」加藤正昭著p49〜p51）

したがって，起電力がある回路でも電位は定義できると 考えています．

広太 さんのレス (2006/10/22(Sun) 21:31)

まずは，電荷のない単純な場合から考えてみませんか． ベータトロンはどうお考えでしょうか． 軸対称な磁場が時間変化する場合には， その軸を囲むようにループ状に誘導電場が発生し，クーロン電場はありません． この場合は，明らかに電位を定義できません． ここまでは，どうでしょう．

ＺＩＧ さんのレス (2006/10/23(Mon) 00:18)

皆さん空間における静電場と回路内の電位を一緒に考えようとしてるようですが，電流が流れている以上静電場ではありません．

私が電位が定義できないといったのは磁束の時間変化がある空間内の電場の保存場である電位は定義できないという意味です．導体，特にコイルのようなもの，の内部のみなら電位を導入できる場合があります．導線を介した位置関係に電場による位置エネルギーを対応させる事ができるのです．（これは両端のつながっていない導体の内部では任意の閉曲線で電場の回転が生じない，rotE=0だからです．） そして例えば上の円状の導線を切断しそこに抵抗を接続した場合，面白い事が起こります． 抵抗Ｒの両端をa,b,導線をＭとし，a->R->b->M->aと誘導電流が流れているとします． 導線中を見た場合，明らかに電位はb->M->aと下がっていきますから,Vb>Va． そして抵抗の両端ではa->R->bと電圧降下が起き，Va>Vb 全体を見れば矛盾が起きているので，この回路全体に電位を導入する事はできません． しかし，重要なのは，円状導線のみだった場合と違い導線部分，抵抗部分だけ見れば電圧はきちんと導入でき，しかも大きさは等しいという事です．これはキルヒホッフの第二法則に他なりません． 全空間においては，電位を設定できなくても，ある部分空間においては，電位を設定できるんです．

（ちなみに蛇足かもしれませんがV=IRという式は抵抗の両端で生じる電圧差においてのみ成り立つ物であり，電圧の関係式です．電位の定義式ではありません．電位の定義は電場の保存場です．V=IRによって電位が定義されているのではありません．）

ゆうすけ４００ さんのレス (2006/10/23(Mon) 00:48)

広太さん

はい，ベータトロンに関して， 完全に同じ考えをもっています．

引き続きの議論，宜しくお願いします．

ZIGさん

a→R→ｂ→M→aと誘導電流が流れているときは， その場合に b→M→a と電位が下がっていくのは怪しいと 僕は思っています． また，V=IRによって電位を定義しているという主張は していないつもりです． 自分の伝え方が下手で申し訳ないです．

いち さんのレス (2006/10/23(Mon) 09:10)

１巻きの円形コイルのどこに起電力があるかという問いは，問いたい気持ちは 分かりますが，どこにあるとしても矛盾するなら，考えてはいけないというこ となんでしょうかね．

ｙama さんのレス (2006/10/23(Mon) 17:58)

-dΦ/dt=IR の右辺の IR は単に 電流×電圧 であって，これを電圧降下と考えるのは適切ではありません． というのは，誘導起電力については，通常の意味での電位を考えることはできないからです．電場がスカラーポテンシャルだけから導かれるとき，そのスカラーポテンシャルを電位といいますが，誘導起電力による電場はスカラーポテンシャルだけからは導けず，ベクトルポテンシャルも考える必要があります．

話がややこしくなるので，ベクトルポテンシャルは考えず，電場と磁場だけで考えましょう． この場合，回路の一部分についての積分 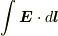をその部分の起電力と考えることができ，それが その部分の IR に等しくなります． 閉じた回路全体を考える場合は，ストークスの定理と 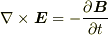を用いれば，この積分は -dΦ/dt となり，これが回路全体の起電力です． 一方，回路の一部分だけの積分は -dΦ/dt の形に書くことはできません． また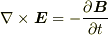， の関係だけでは電場 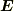は一意的に決まりません．だとすると，回路の一部分だけの起電力というのは無意味だと思われるかもしれません． しかし電場はポテンシャルとは違って不定性なしに決まる物理量です．実際，電場 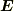は何らかの境界条件を満たしているはずで，その境界条件を考慮すれば一意的に決まることになり，従って回路の一部分だけの起電力も定まります．

初めに書いたように，電流が流れているときには，必ず電位差があるとは限りません．電流が流れているときは電場が存在していますが，その電場を導くような電位を常に定義できるわけではないからです． しかし，起電力は電場が存在していれば上記のように定義できます．

広太 さんのレス (2006/10/25(Wed) 18:22)

ゆうすけ４００さん

多くの方の説明で解決したでしょうか？一応議論の続きをします．

＞はい，ベータトロンに関して， 完全に同じ考えをもっています．

引き続きの議論，宜しくお願いします．

ベータトロンで電位が定義できないのに，なぜ， 磁場が時間変化している空間におかれた，導体の電位が定義出来ると お考えでしょうか？ 電位が定義できない理由は，磁場が時間変化しているからです．

ゆうすけ４００ さんのレス (2006/10/26(Thu) 01:56)

皆様

返信遅れて申し訳ありません． 皆様のお陰で非常に理解が進みました．

丁寧にご指導頂き，本当にありがとうございました！

タケオ 　 さんのレス (2006/10/27(Fri) 20:59)

話は終わってしまったようですが，興味があるので続けて投稿させて頂こうと思います． 1巻きの(何巻きでもいいですが)コイルのどこに起電力があるか，という問題に関してです． コイルの無い場合の電場に関しては，磁場の元となっている電荷の運動についてマクスウェル方程式を解けば得られるでしょう．

次に回路がある場合ですが，電池と抵抗をつないだ回路と，磁場が起電力を作っている抵抗のみをつないだ回路を比較します．

電池と抵抗をつないだ回路の場合，どこに電場があるかと言うと，抵抗のあるところです（電池内部にもありますが）． 電池の場合にも，プラスからマイナスまでの回路の中でどこに電場があってもいいはずです．しかし，抵抗の場所にしか電場はありません．何故でしょうか．

まず，電子の受ける力は常に0としていい，と思います．これは，電子の金属内での（大域的平均）速度の遅さを考慮して（電池一個使い終わって電子は回路を一周もしないのです），v=eEt/m を考えれば，ほぼ正しいと思います． そして，もし抵抗の場所以外に電場があった場合，即座にその電場を打ち消すよう電荷の配置が実現されます．

磁場が起電力を作っている（この言い方はあまり正確ではありませんが）場合も同じように，抵抗のある場所に電場ができると思います． さらに言うなら，電流は回路のどこでも等しく，電子の受ける力は常に0なので，単位長さあたりの抵抗に比例した電場が作られると思います．

以上が私の考えですが，皆様いかがでしょうか．

ｙama さんのレス (2006/10/30(Mon) 15:47)

なるほど，その通りですね． 物質がないときの真空中の電場と，物質（導線や抵抗）があるときの物質中の電場が違うのは確かに当然ですね．

ミュフ猫 さんのレス (2006/10/31(Tue) 00:26)

>しかし，重要なのは，円状導線のみだった場合と違い導線部分，抵抗部分だけ見れ>ば電圧はきちんと導入でき，しかも大きさは等しいという事です．これはキルヒホ>ッフの第二法則に他なりません． >全空間においては，電位を設定できなくても，ある部分空間においては，電位を設>定できるんです．

この説明が良くわかりません． 簡単のため，円状導線の半円部分を抵抗線に置き換えた場合を考えます． 私の考えでは，導線，抵抗線に沿って渦状の誘導電場が発生したとき， 導線と抵抗線のつなぎ目付近で，電荷の偏りが発生すると思います． その偏りによって生じたクーロン電場が，導線内では，誘導電場を打ち消し， 抵抗線内では，誘導電場を強めると思います． その結果，導線内のキャリアの加速が小さくなり，抵抗線内のそれは， 大きくなるので，導線内と抵抗値内の「電流値」が等しくなるのだと思います． 言い換えれば，抵抗値の異なる二領域を流れる「電流値」が等しくなるように， 電荷の偏りが発生して帳尻を合わせるのだと思います． 従って，電荷の偏りで生じたクーロン電場による「見かけの電圧」と， 導線内の端から端へキャリアを運ぶのに要する「仕事」と， 抵抗線内の端から端へキャリアを運ぶのに要する「仕事」の三つの物理量は， 各々すべて値が異なると思います． 私の考えでは，高校物理で扱うコイルを含んだ交流回路において，あたかも， キルヒホッフの第二法則が成り立つように見えるのは，コイルの 「自己誘導起電力」に，コイルの両端に発生する電荷の偏りで生じた クーロン電場による「見かけの電圧」を用いて，式を立てるからだと思います． もちろん，内部抵抗値が０の理想コイルの場合は， 「自己誘導起電力」＝「見かけの電圧」 となるのですが，実際に理想コイルの端から端へキャリアを運ぶのに要する 「仕事」はすべての時刻で０です． なぜなら，理想コイル内の誘導電場を完全に打ち消し合うように電荷の偏りが その両端に発生するからです． 回路の電流値が有限値を取るためには，内部抵抗値が０の回路素子内で， キャリアが加速されてはいけないのです．

以上です．長々，失礼いたしました．m(_ _)m

ｙama さんのレス (2006/10/31(Tue) 18:03)

電荷の偏りによって生じるクーロン電場がコイル内の誘導電場を打ち消すわけではないと思います． 抵抗のかわりにコンデンサーを接続した回路ならば，コンデンサーの極板に帯電した電荷によってクーロン電場が生じ，それが導線内の誘導電場を打ち消すと考えることはできそうです．この場合，誘導起電力の時間的変化がなければ電流は流れません． コンデンサーを抵抗に置き換えた場合でも，導線内ではクーロン電場が誘導電場を打ち消すと考えると，抵抗の帯電量は，それをコンデンサーに置き換えたときの帯電量と等しくないといけません．(ただし，抵抗とコンデンサーの形状や大きさが同じで，抵抗の両端が帯電する場合です．) しかし，この場合は抵抗には電流が流れますが，電流が流れている抵抗の両端に，電流が流れていないコンデンサーと同量の電荷が帯電するとは思えません．

過去ログを見れば分かりますが，抵抗の両端の帯電についてはいろいろが議論がされています．それによると，抵抗の両端の帯電はありうるけれども，ほとんどの場合は無視できるほど小さいようです．

ミュフ猫 さんのレス (2006/10/31(Tue) 21:19)

>抵抗とコンデンサーの形状や大きさが同じで，抵抗の両端が帯電する場合は， >電流が流れている抵抗の両端に， >電流が流れていないコンデンサーと同量の電荷が帯電するとは思えません．

レスありがとうございます．設定を整理します． 同じコイルに対し，互いに形状や大きさの同じ抵抗素子とコンデンサーを用いた RL回路とLC回路において，全く同じ様に，コイルを貫く磁束を変化させ， 強制的にある一定の誘導電場を，発生させます． このとき，抵抗素子の両端に生じる電荷の偏りの電気量と， コンデンサーの極板に帯電する電気量が同じになるはずがない． と言う事でよろしいでしょうか？ 私の考えは，抵抗素子の両端の電気量は，その両端に接続している 導線の形状によると思います． 簡単のため，コイルと導線の内部抵抗値を，抵抗素子のそれに比べて， 極めて小さいものとします． 導線の形状がコンデンサーと同じ極板形状をしていれば， 抵抗素子の両端の電気量は，コンデンサーの極板に帯電するそれと， 同じになると思います． 導線の形状が断面積の小さな細いものであれば，抵抗素子の内部で， 電流はより抵抗値が低くなるような経路を流れるので， 抵抗素子の両端の電気量は，コンデンサーの極板に帯電するそれに比べ， より小さくなると思います． この設定の場合，回路を流れる電流値と，回路素子の両端に生ずる電気量には， 相関性があるのでしょうか？ ちなみに，自慢ではありませんが，私は物理学はド素人ですので， 噛み砕いて，教えてくだされば，非常にありがたいです．(^_^;) 以上です．よろしくお願いします．m(_ _)m

タケオ 　 さんのレス (2006/10/31(Tue) 23:32)

yama様 過去ログを検索した結果

• http://hooktail.maxwell.jp/bbslog/6566.html
• http://hooktail.maxwell.jp/bbslog/6822.html

この2ページを見つけましたが，下側のページに

>これによれば，抵抗Ｒに起電力Ｖの電池をつなぎ電流Ｉが流れるとき，抵抗の両端にＱ＝ＣＶ＝(ερ/Ｒ)Ｖ＝ερＩなる電荷Ｑが滞留することになる．

とあり，抵抗の両端には電荷がたまるという事ではないでしょうか．

また，抵抗の両端にたまる電荷が無視できるほど小さいという記述を見つける事が出来ず，無視できる程小さいというのがどれほど小さいのかわかりませんが，コンデンサーの両端にたまる電荷も一般的なコンデンサー及び電圧の場合μCのオーダーであり無視できる程であると思います．

タケオ 　 さんのレス (2006/11/01(Wed) 00:27)

勘違いをしていたので訂正です．

>とあり，抵抗の両端には電荷がたまるという事ではないでしょうか．

と書きましたが，両端にたまる電荷が，クーロン電場が誘導電場を打ち消すのかどうかが問題でしたね．

失礼しました．

ｙama さんのレス (2006/11/01(Wed) 09:06)

抵抗をコンデンサーに置き換えて考えるというのはちょっと無理があったかもしれませんね．

それはともかく，抵抗0の導線内でクーロン電場が誘導電場を完全に打ち消すとすれば，そのクーロン電場を生じる電荷は，誘導電場の強さと導線の形状・太さ・長さには関係しますが，抵抗の抵抗値には無関係のはずです． しかし，過去ログに記されているように，抵抗両端に滞留する電荷は，その抵抗値に関係します．

ミュフ猫 さんのレス (2006/11/01(Wed) 14:25)

>『詳解 電磁気学演習』（共立出版） の中で誘電率ε，電気伝導率σ， >抵抗率ρの媒質をつめた容量Ｃの平行板コンデンサーの両極間に >電流が流れるとき，合成抵抗ＲはＲ＝ε/σＣ＝ερ/Ｃとなる >という記述を発見し，自分自身の不勉強さを恥じていたところです． >これによれば，抵抗Ｒに起電力Ｖの電池をつなぎ電流Ｉが流れるとき， >抵抗の両端にＱ＝ＣＶ＝(ερ/Ｒ)Ｖ＝ερＩなる電荷Ｑが滞留することになる．

返信ありがとうございます．二つの主張を整理します． まず，一つ目の

>過去ログに記されているように，抵抗両端に滞留する電荷は， >その抵抗値に関係します．

と言う主張の根拠は，上記の過去ログの内容でよろしいでしょうか？ 私もそう思いますが，もう少し詳しく調べてみましょう． 『詳解 電磁気学演習』（共立出版）のP170の問題[20]にある設定は， 平行板コンデンサーに誘電率εの誘電体をつめた回路素子を， 抵抗素子とみなしていますが，本来，導体である抵抗素子のモデルとして， 適当かどうか疑問です． それはともかく，このモデルの場合， Q=ερ(V/R) の式に，回路素子の形状を表す物理量である長さ（l）と断面積（S）を用いた， R=ρ(l/S) と言う式を代入すると， Q=εV(S/l) となり電荷量Qは，抵抗値の要素では，誘電体の抵抗率（ρ）には依存せず， 誘電体の長さ（l）と，それに接続する導線の断面積（S）に依存するようです．

次に，二つ目の，

>抵抗0の導線内でクーロン電場が誘導電場を完全に打ち消すとすれば， >そのクーロン電場を生じる電荷は，誘導電場の強さと >導線の形状・太さ・長さには関係しますが，抵抗の抵抗値には無関係のはずです．

と言う主張が良くわかりません．なぜ，そう思われるのでしょうか？ 私の考えでは，コイル内の誘導電場を打ち消すクーロン電場を生み出す電荷量と， 抵抗素子の両端の電位差をコイルの誘導起電力に等しくするのに要する電荷量は， 互いに独立した物理量だと思います． コイルの両端に生じた電荷の偏りのみがコイルに影響し， 抵抗素子の両端に生じた電荷の偏りのみが抵抗素子に影響するのだと思います． たとえば，二つのコンデンサーを並列にして，ある一定の電圧を加えます． 一方のコンデンサーの電気容量を変化させても，各々の極板に帯電する電荷量が， 常に等しくなると言う事はありえないと思います． 二つの電荷量は互いに独立しています． 各々のコンデンサーにおいて，極板に帯電した電荷のみが， その極板間の電場に影響すると言う事と同じだと思います．

以上です．よろしくお願いします．m(_ _)m

ｙama さんのレス (2006/11/01(Wed) 16:00)

>私の考えでは，コイル内の誘導電場を打ち消すクーロン電場を生み出す電荷量と， >抵抗素子の両端の電位差をコイルの誘導起電力に等しくするのに要する電荷量は， >互いに独立した物理量だと思います． >コイルの両端に生じた電荷の偏りのみがコイルに影響し， >抵抗素子の両端に生じた電荷の偏りのみが抵抗素子に影響するのだと思います．

一般的には確かにその通りですね． しかし次のような場合はどうでしょうか？ 一様な太さの導線でできたコイルがあり，その導線の一部分だけが抵抗をもち，他の部分の抵抗は0であるとします．また，抵抗のある部分の長さ l はコイル全体に比べて十分短いものとします． そうすると抵抗の無い部分の両端に電荷がたまると思いますが，その電荷量は，抵抗の無い部分の誘導電場を打ち消すようなクーロン場を生じるという条件で決まるので，抵抗のある部分の長さ l には無関係のはずです． （厳密には，l が変われば全体の誘導起電力が変化しますが，l が十分小さい場合は，その変化は無視できるでしょう．） 一方，抵抗のある部分の両端にたまる電荷量は Q=εV(S/l) なのでその部分の長さ l に関係します． ところが，抵抗のある部分と，無い部分は互いに接しているので，電荷はその境界部分にたまるはずです．ということは，抵抗のある部分の両端にたまる電荷と，抵抗の無い部分の両端にたまる電荷は同じものだということです． そうすると，抵抗の無い部分の両端にたまる電荷量が抵抗のある部分の長さに関係することになり，矛盾が生じます．

ミュフ猫 さんのレス (2006/11/01(Wed) 17:51)

>抵抗の無い部分の両端にたまる電荷量が >抵抗のある部分の長さに関係することになり矛盾が生じます．

返信ありがとうございます． この主張が良くわかりません．なぜ，そのように思われるのでしょうか？ 簡単のため，設定を以下のように整理します． まず，全長2L+lのコイルにおいて，両端から長さLの部分の内部抵抗値が0で， ちょうど中間の長さlの部分のそれがr(>0)とします． そして，電荷の偏りが生ずる四箇所の位置を端から順にa,b,c,dとします．

a -----------(L)------------- b -(l)- c ------------(L)------------ d

このとき，aの位置の電荷量をQaなどと表すと， Qa+Qd=Qb+Qc=0 となります． 私の考えは，たとえばa-b間のコイルに影響を及ぼす電荷量は，QaとQbではなく， QaとQdであると思います．なぜならば，a-b間ではQbによるクーロン電場は， Qcのそれによって相殺されるからです． 同様に，c-d間のコイルに影響を及ぼす電荷量は，QcとQdではなく， QaとQdであると思います． また，b-c間のコイルに影響を及ぼす電荷量は，QaとQbとQcとQdのすべてです． 内部抵抗が0の部分のコイル内の誘導電場を打ち消すQaとQdは，lに依存しません． 内部抵抗がrの部分のコイルの両端に生ずるQbとQcは，lに依存します． よって，矛盾は起こらないと思います．

以上です．よろしくお願いします．m(_ _)m

ｙama さんのレス (2006/11/01(Wed) 18:20)

どうも状況設定が違っているようですね． 私は，コイル全体が閉じた回路になっている場合を考えていました．つまり，aとd が同一の点である場合です．

しかし，ミュフ猫さんの設定では，aとdはつながっていないので，回路は閉じていませんね．その場合，電流は流れないので，確かにミュフ猫さんの言われるように帯電するでしょうね.

ミュフ猫 さんのレス (2006/11/01(Wed) 20:00)

>どうも状況設定が違っているようですね． >私は，コイル全体が閉じた回路になっている場合を考えていました． >つまり，aとd が同一の点である場合です．

返信ありがとうございます．なるほど，そういう設定でしたか． でも，その場合でもやはり矛盾は起きないと思います． なぜならば，この設定の場合は，

>抵抗の無い部分の両端にたまる電荷量は， >抵抗の無い部分の誘導電場を打ち消すようなクーロン場を生じる >という条件で決まるので，抵抗のある部分の長さ l には無関係のはずです． >（厳密には，lが変われば全体の誘導起電力が変化しますが， > lが十分小さい場合は，その変化は無視できるでしょう．）

と言う主張が成立しなくなるからです． たとえ，コイルの全長に比べ，極めて小さな変位であっても， 電荷の偏りが生じる「つなぎ目」の位置が変化すれば， その電荷量は，大きく変化する可能性があります． つまり，クーロン電場が作る空間では，二点間の電位差が， その経路に依存しないので，二つの経路の誤差が意味を持たないのです． 具体的に，コンデンサーの極板間隔を二倍にすると，同じ電位差にするには， 電荷量を半分にせねばなりません． 二極板間の経路を地球を一周する様に取れば，その経路誤差は無視できます． だからと言って，電荷量の変化も無視できるとは限らないのです．

以上です．よろしくお願いします．m(_ _)m

ｙama さんのレス (2006/11/02(Thu) 08:58)

なるほど，確かにミュフ猫さんのおっしゃる通りですね． 抵抗のある部分の長さによって電荷量が変化することを見落としていました．

電流が流れていても，流れていなくても帯電量が同じになるのが奇妙に思われましたが，よく考えてみると，抵抗が0の部分の電場が0になるのだから，それは当然ですね．

いろいろ御教示いただきありがとうございました．

ミュフ猫 さんのレス (2006/11/02(Thu) 19:52)

>抵抗のある部分の長さによって電荷量が変化することを見落としていました． >電流が流れていても，流れていなくても帯電量が同じになるのが >奇妙に思われましたが，よく考えてみると， >抵抗が0の部分の電場が0になるのだから，それは当然ですね．

返信ありがとうございます． 実際のところ，電荷の偏り云々は，私の想像に過ぎません． 学問の分野では，「固体物理学」や「電子物性物理学」で， 扱われる内容かもしれません． 詳しい方が来られれば，ぜひ，教えてほしいです．

以上です．スレを汚してすみませんでした．m(_ _)m

ＺＩＧ さんのレス (2006/11/05(Sun) 21:44)

ご無沙汰しております． ミュフ猫さん，ゆうすけさんレスいただいたのに，返信できず申し訳ありません． 納得されたようですので，これ以上レスするのもどうかと思いましたが，私なりの返事をさせてもらいたいと思います．

ゆうすけさん＞ 電子がその方向へ動いている以上，電子の感ずるポテンシャルは下がっており，それが運動エネルギーになっていると思われますし，導線内にできる電場の向きからも，電圧は下がっていると見るべきだと思います．

キルヒホッフの法則が成り立つのは（つまり誘導起電力と電圧降下が等しいのは），導体内および抵抗内が一般の空間とは違って電子が一定の密度で存在しているからです． 導体の一部の中の電子が電場によって力を受けてもその電子の前にある電子から反発力を受けます． よって見かけ上電場が打ち消されなくとも回路内の電子の速さは常に同一とみなせると思います．（抵抗で電子が受ける抵抗は回路中の全電子に対して抵抗となる） 厳密には導体や抵抗内で電子の密度差が許される場合，これは成り立ちませんが 現実的には導線や抵抗の材質の問題になりますし，理論的には「導線」「抵抗」の定義問題になります． 理論上の電気回路におけるこれらの定義が実際にどうなっているかは知りませんが，電気回路における諸法則が成り立つには，無視できないような電子の密度差があるとは思えません．（コンデンサにおいても電荷が溜まるのは極板のみで，両端に等量の電化が蓄えられます） 回路内の電子の密度差を認めなければ話は簡単です． 回路の一部にどんなに強力な電場を発生させても，抵抗が繋がれていればそこで電子の速度は一定の値になり，よって回路全体でも一定となります． 電子が等速運動している事から個々の電子が感ずる電場は打ち消されている事が分りますが，それは回路内の電場が常に打ち消されているというのではなく，回路内に有る電子群それ自身が打ち消している（表現がおかしいかもしれませんが）と思われます． 又，抵抗両端で電荷が溜まると密度一定に反しますし， もし電子の密度が偏りを許しても，両端に電荷が溜まるというのには違和感を覚えます． これはばねで連結された多数の物体を考えるとよく分ると思います． ばねで連なって運動している物体間の二つの位置ににあるばねだけが非常に強いエネルギーを蓄えており他のばねには全く蓄えられていないという状況になります， これは抵抗がその両端にのみ集中しているという特殊な状況でなければ考えにくく，通常は周囲のばねにエネルギーが分散してゆくと思われます． 又，ばねが十分強ければこれらの物体は剛体（流体？）とみなせ回路で働く力は全てこの一つの剛体に作用する力と考える事もできます．電磁気力は非常に強い力ですので電子間の反発は相当強くそこからも電子の密度は一定と見るべきではないかと思われます．

更にスレを汚してすみません．ｍ（−−）ｍ

ミュフ猫 さんのレス (2006/11/05(Sun) 23:53)

>見かけ上電場が打ち消されなくとも回路内の電子の速さは >常に同一とみなせると思います． >（抵抗で電子が受ける抵抗は回路中の全電子に対して抵抗となる）

この主張が良くわかりません．なぜ，そのように思うのでしょうか？ 設定を簡単にします． たとえば，同一形状で異なる抵抗値を持つ二つの抵抗素子を， 導線で直列につなげて，両端に電池で一定の電圧を加えます． おっしゃるように，電場が打ち消されず，回路内の電流値が， どの位置においても，常に等しいならば，二つの抵抗素子に加わる， 電圧も等しくなるはずです． なぜならば，回路内には，電池の作るクーロン電場しか， 存在しないことになるからです． しかし，実際には二つの抵抗には，異なる電圧が加わります． つまり，抵抗の両端に電荷の偏りが生じているのです． そして，生じた偏りの電荷量は抵抗素子の両端に接続する導線の形状によります． 断面積の極めて小さな導線であれば，電荷量もほんのわずかです． そのわずかな電荷量が作るクーロン電場が，つじつまを合わせるのに十分な， 電位降下をもたらすのです．

以上です．よろしくお願いします．m(_ _)m

twister さんのレス (2006/11/06(Mon) 01:36)

ミュフ猫さんに：

>そして，生じた偏りの電荷量は抵抗素子の両端に接続する導線の形状によります． 断面積の極めて小さな導線であれば，電荷量もほんのわずかです． そのわずかな電荷量が作るクーロン電場が，つじつまを合わせるのに十分な， 電位降下をもたらすのです．

論点が理解できないのですが，もしそのような電荷分布があるとすれば，どの程度の電気量が発生するか具体的な例で計算していただけますか？

例えば，10Vの電位差を1kΩの抵抗(定格0.5Wなどと決めれば，抵抗線の材質により径・長さを求められますね)に加えた場合を検討されたら如何ですか．そうすれば，抵抗体の両端の位置が決まるのですから，お説に従って電気容量を概算できるはずです．

そんなに簡単に電荷の偏りが発生するならば，コンデンサは無くても良い可能性が出てきてしまいます．また抵抗の高周波特性に大きな寄与をしてしまうように思います．

仮説として，新たなモデルを検討するのはとても面白いことですが，そのモデルに立脚した場合に「実際に起こりえる数量が現実を説明出来るかどうかを検証する」必要があるように思います．

またラフでも良いですから，絵をつけたら如何ですか？

ｙama さんのレス (2006/11/08(Wed) 10:05)

ZIGさんへ

>導体の一部の中の電子が電場によって力を受けてもその電子の前にある電子から反発力を受けます． >よって見かけ上電場が打ち消されなくとも回路内の電子の速さは常に同一とみなせると思います．（抵抗で電子が受ける抵抗は回路中の全電子に対して抵抗となる）

電子は，前にある電子から反発力を受けるのと同様に後方の電子からも反発力を受けるはずです．そうすると，反発力によって電場による力が打ち消されるとは言えません． さらに，電子同士が反発しあうとすると，静電気の場合のように，電子は導体の表面に集まることになるはずです． しかし普通は導線や抵抗の表面が帯電することはありません．それは導体内には電子だけでなく原子核も存在していて，原子核の正電荷と電子の負電荷が全体として打ち消しあっているからです．その結果，原子核からの引力と電子からの反発力が平均的には全体として釣り合うことになり，外部電場による力はそのまま残ります． 電子の速さが平均すると一定になるのは，電子同士の反発力によるものではなく，電子が陽イオン（原子核とそこに束縛されている電子から成り立つ系）と衝突しながら（または陽イオンによって散乱されながら）移動するためだと思います．この過程で電子の運動エネルギーの一部が陽イオンの運動エネルギーになりますが，これは導体全体としてみればジュール熱が発生するということです．

ゆうすけ４００ さんのレス (2006/11/09(Thu) 00:27)

ミュフ猫さんに質問させてください．

2006/10/31(Tue) 00:26 No.12472 に書かれた内容は 理解力の弱い自分にとっても，非常に納得できるものでした． そこで関係した話で，２つほど，質問させてください．

円形の一様な抵抗線を用意して， その抵抗線に沿って渦状の誘導電場が発生した場合には， 電荷のたまりというのは生じないのでしょうか？

もし生じないのであれば，その場合， 誘導電場による起電力Ｖと，抵抗線を流れる電流Ｉと， 抵抗値Ｒとの間で，キルヒホッフの法則 Ｖ＝ＩＲ が成立すると一般的には言われていますが， この法則が成り立つはっきりした論拠というのは あるのでしょうか？

(というのは，個人的には，このキルヒホッフの第二法則は 運動方程式と同じものであり， 論拠なき基本法則だと思っているからです． つまり，電流が流れるから，電流値×抵抗値という，１Ｃあたりの エネルギー損失がある”はず”で，それは，起電力と 等しいという基本法則がある．と思っているからです．）

以上，お手数ですが宜しく御願い致します．

ミュフ猫 さんのレス (2006/11/09(Thu) 01:47)

ゆうすけ４００さん，こんばんは． 今，これらの分野の理論を調べています． 私自身，混乱していますので，考えをまとめてから書き込みます． 皆さんにお願いします． 面白い解説を発見しました．ぜひ，本屋で立ち読みして（ｗ）ください．

「理論電磁気学第３版」砂川重信著（紀伊国屋書店発行）

第５章定常電流§５定常電流の分布（P142〜P147）

これに記された説明では，誘電率と電気伝導率との比によっては， 電気伝導率の異なる二つの導体の境界面上に表面電荷が蓄積されるそうです．

にしても，プロ・セミプロの方．このスレをご覧になっているのなら， そろそろ助け舟を出していただけないでしょうか？(ToT)

以上です．よろしくお願いします．m(_ _)m

ｙama さんのレス (2006/11/09(Thu) 15:49)

円形の一様な抵抗線の場合は一様な電場が生じるのでどこにも電荷は溜まりません． 従ってクーロン電場は無く，誘導電場だけが存在します． 局所的なオームの法則 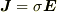を抵抗線の体積全体で積分すれば V=IR が導かれます． ただし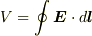， は抵抗線全体に加わる誘導起電力です．

・・・と言うことができると思うのですが，きちんとした解説はミュフ猫さんに期待します．

次に V=IR についてですが，この式の抵抗値 R とは何でしょうか？ 抵抗とは電流の流れにくさのことで，具体的には，電流を流すのに必要な電圧の単位電流当たりの値として定義されると思います．すなわち R=V/I です． ということは V=IR は抵抗値を定義する式であって，法則とは言えないと思います． もし抵抗値 R が（V=IRとは全く無関係に）別の方法で定義され，その R について V=IR が成り立つことが実験的に確認されれば，それは法則と言えるでしょうが・・・．

ゆうすけ４００さんは

> つまり，電流が流れるから，電流値×抵抗値という，１Ｃあたりの
>エネルギー損失がある”はず”で，それは，起電力と
>等しいという基本法則がある．

と考えていらっしゃいますが，それは基本法則ではなく，その関係が成り立つように抵抗値というものが定義されているだけのことです．

抵抗に関係した法則としてオームの法則がありますが，これは電圧と電流が比例するという法則ですから，その比例定数である抵抗値は定数になります．すなわち，V=IR の R が定数になるという法則です．これは実験的に導かれた法則であって定義ではありません． 定義ではないので，厳密に成り立つわけではなく，半導体などでは R が定数でなくなります．

また，ゆうすけ４００さんは，V=IR をキルヒホッフの法則とされていますが，ちょっと違うように思います．キルヒホッフの法則は，閉じた経路についての電圧降下の和が，起電力の和に等しいという内容だと思います．

ゆうすけ４００ さんのレス (2006/11/09(Thu) 16:33)

＞ミュフ猫さんへ，

宜しく御願いします．

＞yamaさんへ

おっしゃっている意味がよくわかりません． 僕はあくまでＶは，誘導電場による起電力（つまり誘導起電力）の つもりで述べています．

従って，(見た目は紛らわしいですが）Ｖ＝ＩＲは オームの法則(抵抗の定義式)のつもりでは述べておりません．

Ｒは一様な抵抗線の抵抗であり，そのままの意味です．

ｙama さんのレス (2006/11/09(Thu) 17:17)

その一様な抵抗線の抵抗 R が R=V/I で定義されるわけです． ただし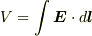， です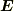． はクーロン場であっても誘導電場であってもかまいません． V はクーロン場の場合は電圧，誘導電場の場合は誘導起電力といわれますが，どちらも電場を抵抗線に沿って線積分したものです． ただし，クーロン場では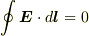， が成り立ちますが，誘導電場では成り立ちません．

と書いてみたものの，もしかするとゆうすけさんが考えておられる抵抗の定義が私の定義とは違っているのかもしれませんね． ゆうすけさんは抵抗をどのように定義されているのでしょうか？

ゆうすけ４００ さんのレス (2006/11/09(Thu) 19:04)

抵抗の値は，既に何らかの別の実験で求めてある，ということが僕の議論では前提としています．その上で，その抵抗に誘導起電力をかけた場合に，どのような電流が流れるのかという問題を考えているとしてください．（そもそもここの考え方が間違っているような気もしますが．．）その場合に立式するべき式は，「起電力が，電流×抵抗値に等しい」というキルヒホッフの第二法則であり，誘導起電力Ｖと，抵抗値Ｒから，流れる電流Ｉを求めるべく，Ｖ＝ＩＲと立式するべきではないかと考えています．

あまり良い例ではないかもしれませんが，上で述べた，その別の実験例について述べます．例えば，一様な円形の抵抗線を，まずハサミでいったん切り，両端のある状態にします．その両端に，ある値の電圧をかけ，流れる電流値を測定します．そこから，抵抗値を割り出します． その後で，この誘導電場をかける問題を考えているという状況を考えています． （切断の影響は無視できるという立場にたっちゃっていますが．電流の流れにくさを表す指標が抵抗なので，これでもよいと思っています．）

とはいえ，うーん，，この文章を書きながら，抵抗の定義式を，電圧÷電流ではなく，yamaさんのおっしゃる通り，電場の線積分値÷電流としてしまえば，僕の混乱は解決されそうな気配もしてきました．つまり，キルヒホッフの第二法則を基本法則としてくみ上げなくても理論が閉じるのでは，，と考え出しました．とはいえ，まだよくわからないです．．混乱したまま文章をかいてしまっていますが，お許しください．

yama さんのレス (2006/11/09(Thu) 23:22)

まず V=IR という式が何を表しているのかを明確にしておかないといけません． R に何の条件もついていなければ，これは抵抗 R の定義式です． この R が定数であるという条件がつけば，これはオームの法則です． これは１つの抵抗について成り立つ法則ですが，キルヒホッフの第2法則は，これを多数の抵抗を含む回路に拡張したものです． オームの法則は局所的には 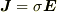と表されます．実際これを積分すれば V=IR が得られます． 局所的な関係のほうがより基本的であると考えられますが，局所的なオームの法則は電流密度と電場の関係です．したがって，その電場がクーロン電場か誘導電場かには無関係に，ベクトルとして等しい電場は，当然同じ電流密度を生じるはずです．そうだとすると，これを積分した V=IR もクーロン電場か誘導電場かに無関係に成り立つはずです． もちろんVはどちらの場合も電場の線積分です．

ゆうすけ４００ さんのレス (2006/11/10(Fri) 00:42)

>R に何の条件もついていなければ，これは抵抗 R の定義式です． この R が定数であるという条件がつけば，これはオームの法則です．

ここまでは納得できます．大丈夫です．

＞オームの法則は局所的には j=σE と表されます．実際これを積分すれば V=IR が得られます．局所的な関係のほうがより基本的であると考えられますが，局所的なオームの法則は電流密度と電場の関係です．したがって，その電場がクーロン電場か誘導電場かには無関係に，ベクトルとして等しい電場は，当然同じ電流密度を生じるはずです．そうだとすると，これを積分した V=IR もクーロン電場か誘導電場かに無関係に成り立つはずです．もちろんVはどちらの場合も電場の線積分です．

ここでまず基本的な質問をさせてください． だとすれば，一般的には，j=σＥは，σの定義式と考えてよいのでしょうか？ つまり，Ｖ＝ＩＲが， (i)一般の場合→Ｒの定義式(ii)Ｒが定数→オームの法則 であったのと同様に，j=σＥも， (i)一般の場合→σの定義式(ii)σが定数→オームの法則 といえるのでしょうか？

twister さんのレス (2006/11/10(Fri) 01:58)

横から失礼します．

私は若かりしころ，「電流密度 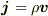が電場 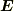に比例する」のが腑に落ちませんでした．

でも，ミリカンの実験を見ているうちに，重力による等加速度を受ける油滴が等速度運動する事を知って，電流が電場強度に比例するのを納得した覚えがあります．また，当時，金属中の古典電子論の本に，

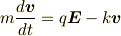
といった感じのモデルの説明が在りました．私は，電子と言えども，金属中で摩擦力的な抵抗(抗力)を受けるのに驚きましたが，どうせ物性物理では細かな量子力学的な計算があろうかと思い，それ以上追求しませんでした．

しかし，摩擦力のような存在があれば，発熱(ジュール加熱)も説明できるし，終速度が電場に比例するというのが説明できるので大いに感激しました．

根が単純なので，そのまま何十年と過ごしてしまいましたが，皆さんの論議を拝見して，昔の記憶が蘇えって来ました．

恐らく,高温超伝導現象などが多角的に研究されている現在ですから，通常の伝道現象も，超伝導の相転移みたいな観点から色々な理論計算があるようにも思いますが...．ここら辺のご説明もできれば解説していただきたいものですね．

yama さんのレス (2006/11/10(Fri) 07:16)

ゆうすけさんが書かれたように考えていいと思います．

Stromdorf さんのレス (2006/11/10(Fri) 07:48)

↓こんな本が出ているようですね．まだ読んでませんが，面白そうです．

• http://pub.maruzen.co.jp/shop/462107024X.html

twister さんのレス (2006/11/10(Fri) 10:57)

yamaさん：

>ゆうすけさんが書かれたように考えていいと思います． 論議の進展を拝見したいと思います.

Stromdorfさん：

>こんな本が出ているようですね．まだ読んでませんが，面白そうです． ご教示感謝します．一度拝見してみます．

ゆうすけ４００ さんのレス (2006/11/10(Fri) 23:26)

としますと，一般的に言って， 回路に成り立つキルヒホッフの第二法則は，σの定義式を回路に沿って線積分したものである． ということでしょうか？

yama さんのレス (2006/11/11(Sat) 00:58)

誘導電場とクーロン場だけならそう考えていいと思いますが，電池がある場合は違った取り扱いが必要だと思います． 電池内部では低電位から高電位に向かって電流が流れるので，電池内部ををクーロン場と考えることはできません．電池内部の化学反応の結果このような流れが生じるわけです． 電池内部のことは考えないものとして電池のはたらきだけに注目すると，電池のはたらきは電位差をつくりだすことなので，その電位差を電池の起電力というわけです． 閉じた回路を１周する場合，抵抗による電圧降下を打ち消すだけの電位差が電池によってつくられないといけません．その電位差は起電力の和なので，起電力の和が電圧降下の和に等しいというキルヒホッフの法則が成り立つことになります．

ゆうすけ４００ さんのレス (2006/11/11(Sat) 18:24)

うーん，また色々混乱し始めましたので２つ程基本的な質問をさせてください． １電場の定義を教えてください． ２電場には，クーロン電場と誘導電場以外のものは存在するのでしょうか？ 以上，宜しく御願い致します．

yama さんのレス (2006/11/11(Sat) 20:38)

１荷電粒子にはたらく力が 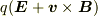と表されるようなベクトル場 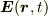を電場というのだと思います．

２マクスウェル方程式によると，電場は電荷分布と磁場の変化によって決まります．前者によるものがクーロン場，後者によるものが誘導電場なので，これ以外のものは存在しないと思います．

ゆうすけ４００ さんのレス (2006/11/11(Sat) 23:14)

なるほど．ありがとうございます．続けて質問させてください．

電池内部では，クーロン電場に逆らって，電荷は移動していると思います． とすると，その電荷は(化学反応由来ではありますが)何らかの力を受けていると思います．

その力は一体何なのでしょうか？ (電荷が力を受けているので)それは電場によるものではないのでしょうか？

ミュフ猫 さんのレス (2006/11/11(Sat) 23:30)

皆さん，こんばんは． 混乱させて申し訳ありませんが，クーロン電場（静電場）と誘導電場以外にも， 電場が存在すると思うのです． ただし，上記の二つでは説明しきれない電場という意味で言えばです． 厳密には，電荷の運動が電磁場の分布を作る訳ですから， 「電荷量に依存する電場分布」 「電荷量と電荷の速度に依存する電場分布」 「電荷量と電荷の加速度に依存する電場分布」 の三つの電場に分けられると思います．説明できないものは，二番目の電場です． まず，その内部に定常電流が存在する直線状の導線の近傍の空間において， 点電荷が静止していれば，それに力が及びます． 導線が電気的に中性で，電荷の偏りも無いとすれば，クーロン力ではありません． また，定常電流が作る電流磁場は静磁場なので，誘導電場も存在しません． もちろん，静止している点電荷にはローレンツ力も及びません． つまり，平行な二本の直線状の導線の一方だけに電流を通すとき， もう一方の導線は，帯電していれば引力か斥力を受け，電気的に中性であっても， 静電誘導を起こします． ところが，定常電流を作るキャリア電子の（平均）移動速度の半値で， 点電荷が運動していれば，力を受けません． これは，電荷が等速直線運動するときに，周りの空間に作られる電場の分布が， 静止状態のときのそれに比べ，やや歪むからです． ひずみ具合を誇張して言えば，静止状態のときの等電位面が， 球面形状であるのに対し，等速度運動のときのそれは， ラグビーボールの表面のような楕円球面形状になります． この二つの電場の差の分布が， 「電荷量と電荷の速度に依存する電場分布」 です．

私はこのように理解してます．(^_^;) 横レス失礼しました．m(_ _)m

ゆうすけ４００ さんのレス (2006/11/12(Sun) 00:14)

ミュフ猫さん，こんばんはです．

＞まず，その内部に定常電流が存在する直線状の導線の近傍の空間において， 点電荷が静止していれば，それに力が及びます．

自分の理解力が弱く，この文の意味がとれず，よくわからないです．その結果

＞つまり，平行な二本の直線状の導線の一方だけに電流を通すとき， もう一方の導線は，帯電していれば引力か斥力を受け，電気的に中性であっても， 静電誘導を起こします．

の文の意味もよくわかりません．もう少し詳しく教えて頂けないでしょうか？

ミュフ猫 さんのレス (2006/11/12(Sun) 00:58)

ゆうすけ４００さん，こんばんは．

電荷が等速直線運動するときに，周りの空間に作られる電場の分布が， 静止状態のときのそれに比べ，やや歪むと言うのはよろしいでしょうか？ もし，この部分が引っかかるようでしたら，「電磁気学」の専門書を 読んでほしいのですが・・・． と言うのも，この結果を得る計算は，かなり骨が折れる作業なのです． もっとも，運動する電荷が作る電磁場の分布は， 「電荷量に依存する電場分布」 「電荷量と電荷の速度に依存する電場分布」 「電荷量と電荷の加速度に依存する電場分布」 の三つの電場に分けられると言う結果を得る作業は，もっと大変なので， この説明を要求されるのも，大いに困るのですが・・・． 取り敢えず，上記の結果を受け入れていただけることを前提に， 大雑把に説明します． 点電荷から見た観測系において，導線内のキャリア電子と正イオン（原子核） の速さの差がポイントになります． より速い速度で運動しているように見える方の作る電場が，より強くなります． よって，静止している点電荷から見た観測系では，キャリア電子の作る電場が， 正イオンの作るそれより強くなるので，力を受けます． また，力を受けないようにするには，互いの速さが同じに見える観測系 に立っていればよい訳ですから，キャリア電子の半分の速度で運動するとき， 点電荷は力を受けなくなります．

以上です．よろしくお願いします．m(_ _)m

yama さんのレス (2006/11/12(Sun) 01:40)

ゆうすけさんへ

電池内部ではイオンが移動しますが，これは電気的な力によって，すなわち電場からの力によって移動するのだと思います．つまり電池内部では負極から正極に向かう電場ができていると考えられます． しかし，その場合，電極のところで電位が不連続になってしまいます． この不連続性は，電子が金属表面から飛び出すときの仕事関数に起因すると考えられます． 両極の金属の仕事関数の差が，接触電位差であり，それが起電力になると考えられます． 仕事関数はポテンシャルの壁なので，この壁を乗り越えるにはエネルギーが必要です．化学反応によって放出されるエネルギーがこれに当てられるわけです．

次に，クーロン電場と誘導電場ですが，ミュフ猫さんのご意見を参考に考え直してみたところ，電場をクーロン電場と誘導電場などに分けるのはあまり意味がないように思えてきました． 確かに，磁場がなくて静止した電荷だけがある場合はクーロン場で，電荷がなくて磁場が変化している場合は誘導電場だと考えることができます． 前者は 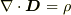によって，後者は 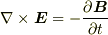によって決まります． しかし，運動する電荷の作る電場は，これらのどちらか一方の式だけでは決まりません．これら２つの式に加えて，これ以外ののマクスウェルの式も必要です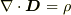． 「 によって決まる電場と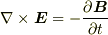， によって決まる電場の２種類の電場があって，それを加えたものが運動する電荷の作る電場である．」と考えるのは間違いです． つまり，電場は同時に両方の式を満たすのであって，片方の式だけを満たす２種類の電場の重ね合わせではありません．

ゆうすけ さんのレス (2006/11/12(Sun) 02:12)

ミュフ猫さんへ

はい．おっしゃる通りです．情けないことに電荷が等速直線運動するときに，周りの空間に作られる電場の分布が，静止状態のときのそれに比べ，やや歪むというところで，ひっかかっています．これは自分の勉強不足によるものなので，勉強したいと思っています．ちなみにどういった本に載っているものかを教えて頂けると嬉しいです．ジャクソンぐらいまで読まなくちゃいけないレベルなのでしょうか？

yamaさんへ

>電池内部ではイオンが移動しますが，これは電気的な力によって，すなわち電場にからの力によって移動するのだと思います．つまり電池内部では負極から正極に向かう電場ができていると考えられます． ということは， 電荷が力を受けるということはそこに必ず電場が発生している，という立場にたつべきということでしょうか？

（電場Eはf＝q(E+v×B)をみたすものとして，（ファイマンの教科書等）力をもとによく定義されています．ただし，電荷が力を受けたら，それは全て電場によるものという考えには個人的に疑問をもっています．というのは，例えば電荷が純粋に力学的な力を受けたとしたら（例えばヒモをつけてひっぱる），それは明らかに電場ではないだろうと考えているからです． ということは，電荷に働いた力を，それが電場によるものか，そうでないかを区別するべき何らかの基本的な要請がどこかにあるのではないかと個人的には思っています．とはいえ，それは何なのかということも，そもそもそんなものが存在するのかということも，もっと言えば自分の考えは果たして的を得ているかどうかもさっぱりわかっていないの状態です．）

ミュフ猫 さんのレス (2006/11/12(Sun) 02:32)

ゆうすけ４００さんへ

大抵の専門書に載っていると思います． 「ファインマン物理学?〜電磁気学〜」（岩波書店） 「理論電磁気学第３版」（紀伊国屋書店） など，有名どころには載っています．

以上です．よろしくお願いします．m(_ _)m

yama さんのレス (2006/11/12(Sun) 09:56)

電荷をもつ粒子には電磁力の他に重力もはたらきます．電磁力は電荷に比例し，重力は質量に比例することで区別できます． といっても１つの荷電粒子にはたらく力を調べるだけでは，これらを区別することはできないでしょう．しかし比電荷の異なる荷電粒子にはたらく力を調べれば，電磁場と重力場を区別できると思います． ヒモで引く場合は，ヒモ自体がいろいろな荷電粒子でできているので，微視的に考えれば，電磁的な力に還元できると思います．

運動する電荷の作る電場は，一般には遅延ポテンシャルを用いて計算され，その結果，電場は速度に関係することになります．つまり遅延効果によって速度に関係する電場が生じるわけです． 等速直線運動の場合に限れば，静止している電荷のつくるクーロン場をローレンツ変換することによっても求められます．その結果は当然ローレンツ変換のパラメータである速度に関係することになります．等電位面が歪むのはローレンツ短縮によるものと考えられます．

広太 さんのレス (2006/11/12(Sun) 18:09)

興味深く議論を読ませて頂いてます．

ゆうすけ４００さんが出した疑問， 「電池の中で電荷が受けている力の源」についてみなさんの意見を聞きたいです． 化学的な力や，と記述されている場合がおおいのですが， ローレンツ力であることは間違いないと思いますが，その電場または磁場の源は何なのでしょうか？ ミュフ猫さんのいう３っつのうちどれにあたるか意見を聞きたいです．

ゆうすけ さんのレス (2006/11/12(Sun) 19:20)

遅延ポテンシャル関係でしたか．．まさに勉強していないところです．時間が取れ次第，教えて頂いた本で(両方持ってます)勉強したいと思っています．本当に情報ありがとうございます．

はい，広太さんと同じく，僕も電池の中で電荷が受けている力の源が気になります．ご意見をお聞かせ下さい．yamaさんのおっしゃる通り，電荷に比例するか否かが，その力が電磁場による力と呼べるか否かの大きな選択則かもと思います．ただ，それだけでは不十分な気もします．また，仮にそうだとした場合に，化学反応による力は，電磁場による力かどうかは，疑問が残っています．というのはその力が電荷に比例する力かどうか判断がつかないと思えるからです．

yama さんのレス (2006/11/12(Sun) 23:39)

上で「遅延効果によって速度に関係する電場が生じる」と書いたのは適切でなかったかもしれません． 運動する電荷について遅延ポテンシャルを計算するとリエナール・ヴィーヒェルトのポテンシャルといわれる速度を含む式が得られるので，それから導かれる電場が速度に依存することになります． しかし速度自体は時刻のずれに直接には関係していないので，遅延効果というのは適切でないように思います． 電場が速度に関係することはローレンツ変換で考えるほうが分かりやすいかもしれません．

次に電池の中で電荷が受ける力ですが，化学反応は電極の表面で起こります．従って電極の表面付近を除けば，イオンにはたらく力は，普通に電場からはたらく力と考えていいと思います． 電極表面でおこる原子のイオン化やイオンと電子の結合などの化学反応のときに電子やイオンにはたらく力も基本的には電磁力だと思います． しかし古典論では化学結合をうまく説明できないので，当然ながら量子力学的な取り扱いが必要です．その結果離散的なエネルギー準位とかパウリの原理などに基づいて化学結合が説明されます． 電池の反応もこのような化学結合の理論に基づいて説明されると思います． といっても具体的な説明は私にはできませんが・・・．

その電磁力ですが，量子化学では普通は単なるクーロン場と考えてシュレーディンガー方程式を解きます．もちろん厳密には解けないのですがいろいろな近似をすることによって，実測値に近いエネルギーが算出されるようです．

なんとなく さんのレス (2006/11/12(Sun) 23:43)

みなさん，こんばんは．なんとなくです． 解説には遠いですが意見を言うだけで良いなら，私の考えも言わせて下さい．問題は元々の主題と懸け離れたようですが，電池内部の物理的様相について何を知りたいのか岡目八目と雖も不明です．電池内部の化学的反応がいかに複雑であれ，プロセスが不明であれ，電磁気力であることは疑いの無いことです．プリミティブな説明ですが，現代物理学では全ての力は弱い力，重力，電磁気力，強い力のいずれかに還元されますが，エネルギーレベルからして有意なのは電磁気力しかあり得ないからです．ひもで引こうが棒でつつこうが，電磁気力です．素過程（素粒子レベルまで微視的に反応を追うこと）を見たとしても，電子や正孔，格子の集団振動との多粒子相関力があるにしてもその正体は電磁気力に起因します．そしてそのようなレベルで説明が欲しいなら，既に電磁気力のみでは説明が不可能です．これは矛盾するようですが，第二量子化と呼ばれる量子論が不可欠となります．なぜならそのような微視的領域では量子電気力学効果による現象が支配的となるからです．更に言えばそのような力には軌道角運動量やスピンの相互作用が含まれているからですが，それも電磁気力の一種です．ただし，古典電磁気学では説明できません． それでマクロな電磁気学では電池を一様なポテンシャル，起電力と内部抵抗に置き換え結果として計算と実験（測定）結果が合うように，或いは合うことを確認して回路理論を組み立てているのではないでしょうか．これらを踏まえて電池内部での相互作用のどのレベルが必要なのか再考する必要があります．私には元々の問題から言って，それはまた別の話，という気がしますが・・・．長々駄文，失礼しました．

なんとなく さんのレス (2006/11/12(Sun) 23:57)

>yamaさん

すみません，かぶっちゃいました．でも結論が似てた（と思うけど）ようなので，ちょっと安心．量子化学でクーロン場とするのは単体近似でしょうか．物理でのハートリーフォック近似が基本である様なものかなあ．量子化学は習ったことがないので良く知りませんが，フロンティア軌道法などをみると量子物性論とはまた違ったアプローチのような．どちらにしても手が出ませんが．

広太 さんのレス (2006/11/13(Mon) 00:34)

何が知りたいかと言えば，電池の中の電場が何者かということです． クーロン電場では，起電力は発生しない．しかし，誘導電場が発生しているとも思えない．これが，疑問でした．

そしてその解答は，私の力では読み取れないのですが，

yamaさんは，クーロン電場と答えていて（量子力学は用いるが古典電磁気学で説明されてる）

なんとなくさんは，古典電磁気学では説明出来ないものであり，量子電気力学で説明できる． 私には同じことを言っているとは見えないです．

かなり込み入った話だとおもうのですが，なにか参考文献を示して頂けると嬉しいです．

なんとなく さんのレス (2006/11/13(Mon) 04:07)

解説では無いと断ったのですが，不親切な表現だったかも知れません．ずばり解決できるような文献は知りませんので，もう少し表現を変えてみますね．まず，前にyamaさんも言われたようにクーロン場と誘導電場を区別することにあまり意味があるとは思えません．電場に種類があるわけではなく，その起因に違いがあるだけだと思います．では電池内部では何が起きているか．イオン化傾向の大きく異なる２枚の電極が伝導性の液体中に近く置かれている．電極表面から電極物質がイオン化して溶け出す．イオン化するとは電子の放出またはキャプチャですが，これは量子力学的に説明される．電子が移動するが連続せず，すぐ止まる．少し語弊がありますが電場のためではない．このとき電子に与えられるエネルギーが化学的エネルギーと呼ばれている．電極間に電場があるかと言えば無いでしょう．もちろん電流も流れていません．つぎに電極間を導線でつなぐ．そうすると初めて電極では電子の供給が連続し，ドミノ倒し的に電流となって電子の移動が連続する．ここで初めて電極間に電位差が生じたことになり，それは電流×電池内部抵抗で表される．起電力はそのように回路をつなげば電流をおこすことの出来る潜在的能力を指すので，電場が起電力を発生させるわけではない． しかし先述のイオン化を起こす力はやはりクーロン場であり，語弊があると書いたのはそのためです．このとき誘導電場？なるものはどこにもありません．これが私の思っている描像ですので，何を求めているのか分からないというのはその文脈に沿ってです．質問の意図を勘違いしているか，私の描像が間違っていたら申し訳ないですが，あくまで私の意見です．

ｙama さんのレス (2006/11/13(Mon) 14:08)

なんとなくさんの説明でいいと思いますが，少し補足しておきます． 広太さんは電池内部も含めて回路全体がクーロン場であれば，電流が循環するはずはないと考えられたのでしょう． 確かにクーロン場だけならば，電子が循環することはありませんし，電池を含む回路でも電子が循環するわけではありません． 電池内部では電子ではなく，イオンが移動することによって電流が流れます．つまり電子は循環しないのですが電流は循環することになります．

化学反応が単純なダニエル電池について考えてみます． 負極では亜鉛原子がイオン化し，電子を放出します．その電子は導線や抵抗を通って正極に移動します．（実際に１つの電子が負極から正極まで移動するかどうかは疑問ですが・・・．） 正極では，電子が表面近くの銅イオンと結合して銅原子となり，その銅原子は正極に結合します．つまり電子は負極から正極まで導線中を移動するだけで，循環するわけではないのです． 反応が進むとだんだん溶液中の銅イオンと負極の亜鉛が減少し，どちらかがなくなると電流が流れなくなります． つまり，電池ではイオンや原子として蓄えられた電荷（とそれにともなうエネルギー）を電流（のエネルギー）として放出するわけです．その点ではコンデンサに似ているようにも思えます． 正極と負極の反応を合わせると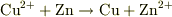， となり，この反応で放出されるエネルギーが起電力の原因です． この反応では，イオンと電極との電子のやり取りが電極表面を通じて行われるため，電極の金属の仕事関数がエネルギーに関係してくることになります．

エネルギーを具体的に計算するにはシュレーディンガー方程式を解く必要がありますが，電磁場を量子化する必要はないので量子電気力学を用いる必要はないでしょう． 量子電気力学が必要なのは，電子の対生成や消滅などの高エネルギー現象を扱う場合です．もちろん低エネルギーの現象でも精密な計算には量子電気力学が必要で，水素原子のラムシフトがその例です． しかし，多電子問題ではシュレーディンガー方程式でも近似的にしか解けないので，量子電気力学を用いる意味はほとんどないと思います．また，正確な計算ができたとしてもエネルギーがわずかに変わるくらいでしょう． 量子化学の計算についてはあまり具体的なことは知りませんが，ハートリーフォック近似はよく用いられるようです．

なんとなく さんのレス (2006/11/14(Tue) 09:00)

>yamaさん いつもフォローをありがとうございます．

仰るとおり「量子電気力学」は確かに筆が滑りました．ここに撤回します． 申し訳ない．言い訳すると，夜中でテンション上がりすぎました． では，また．

広太 さんのレス (2006/11/15(Wed) 09:54)

ありがとうございます．納得しました．

実際の電池は，いつか電流が流れなくなる． だから，電子が循環しているわけではない，広ーい意味ではコンデンサーと同じような仕組み．だから，クーロン電場でいいわけですね．

ぼくも，高校生に物理を教えることがあるのですが，そのときキルヒホッフの法則を「一周すると電位差は０」と教えていて，後ろめたかったのですが，電池においては正しいわけですね．誘導電場があるときは微妙ですが．．．

このことについては，時間があるときにまた書き込みします．

ゆうすけ さんのレス (2006/11/25(Sat) 15:18)

返信遅くなってすみません．ゆうすけ４００です．

皆様の丁寧なご指導のお陰で，自分の理解がまた一段と進みました．本当にありがとうございました．また，何かわからないことが生じたときに質問させてください．宜しく御願い致します．