SATA_YUKI さんの書込 (2006/09/03(Sun) 23:22)

回転する円盤状で物体を観察すると，物体に見かけ上の力であるコリオリ力が働くことは理解できています．ある本の中で『回転する円盤状で中心から外に向かって等速直線運動をする物体を観察すると，コリオリ力が働くため，その物体は等速直線運動ではなく，等速円運動になる』とありましたが，なぜ，等速円運動になるのかが理解できません．自分なりに図を書いてみたのですが，物体自体は等速直線運動をしているので物体は円の中心からどんどん遠ざかり，コリオリ力が働いても円にはならないと思うのです．いかがでしょうか？本が間違っているとは思えませんし・・・． もし宜しければアドバイスいただければと思います．

yama さんのレス (2006/09/03(Sun) 23:50)

等速円運動にはならないと思います． コリオリ力だけなら，等速円運動になると思いますが，回転する座標系ではコリオリ力のほかに遠心力もはたらくからです．

komagatake さんのレス (2006/09/04(Mon) 08:58)

おはようございます．ｋｏｍａｇａｔａｋｅです．

図を書かれたということですがそれで判断されてはどうですか．遠心力とかコリオリ力とかの座標系の読み替えにより生じる力を入れるとややこしくなります．

２枚のｘ−ｙ平面が重なっているとして下さい．上の平面のｙ方向に物体が等速度で運動しているとします．一定時間毎の位置をプロットします．Ｐ１，Ｐ２，Ｐ３，・・・とします．下の平面に円盤を置きます．中心は原点とします．この円盤状に上の面と同じ点を書きます．Ｑ１，Ｑ２，Ｑ３，・・・とします．円盤が一定の角速度で回転しているとするとＱ１，Ｑ２，Ｑ３，・・・も一緒に回転します．それに伴ってＰＱの距離も大きくなっていきます． 物体がＰ１に行ったときの距離はＰ１Ｑ１です．これをａとします．物体がＰ２に行ったときの距離はいくらでしょう．Ｐ２Ｑ２＝４ａです．Ｐ３Ｑ３＝９ａです．回転する円盤にＰ１，Ｐ２，Ｐ３，・・・の位置を写したものをＰ１’，Ｐ２’，Ｐ３’，・・・とします．円盤状の固定点からＰ１’，Ｐ２’，Ｐ３’，・・・を見た物が観察される運動です．

中心からの半径方向の距離は一定の割合で増加していきます．円周上を回転方向とは逆にずれていきます．ズレの大きさは１，４，９，と増えていきますから等加速度運動に対応します．円周に沿っ方向に重力が働いている放物運動のようなイメージですね．円周に沿った方向に加速されているように見えるから対応する力を考えたのがコリオリ力です．中心からの距離が増えていくので一定の角速度で回転していても円周に沿った方向での移動距離が加速度的に変化するのです．コリオリ力の説明の場面です．

中心からの距離の変化は加速度的ではありません．対応する力を考える必要はありません．

遠心力は円盤と一緒に運動している物体に対して働いているとしている力です．円運動は加速度運動であるのに観測者の立場から静止系に読み直しています．静止だから釣合の力が必要になります．この力の大きさは質量×向心加速度と同じになりますが意味が違います．

釣り合いが破れて飛び出していったときの運動を遠心力による運動と見たくなるかも知れませんが運動方程式の中に入ってくる力にはなれません．

何かの事情で物体が中心からある距離離れたところで止まっているとします．その時は回転する円盤の上から見れば回転の方向と逆向きに等速で円運動していることになります．

円盤と物体との間に摩擦があればどうなるでしょうか．中心から離れるにしたがって円盤との間の相対速度は大きくなっていきます．速度に比例する抵抗のある場合の放物運動に似てきます．終端速度に対応するところから等速円運動になります．地表と大気の間での摩擦は粘性抵抗と同じ物と考えてよいでしょうから気象の分野ではこの結果が期待される場面があるでしょう．

中心から離れる運動は遠心力，円周に沿っての運動はコリオリ力と考えている人が多いように思いましたので初歩的な方法で説明を試みてみました．

ｙama さんのレス (2006/09/04(Mon) 16:23)

確かに，等速円運動にならないことは，図を書いてみれば明白ですね． しかしSATA_YUKIさんの疑問は，等速円運動になるかどうかということはもちろんですが，本の記述との食い違いの原因にも疑問を持たれているのだと思います．その原因が遠心力なのですが・・・． しかし，それについての詳しい考察は高校物理では必要ないものと考えて，遠心力が原因であることを指摘するだけにとどめたわけです．

実際きちんと説明しようとすると，いろいろややこしい問題が出てきます． 回転基準系で生じる慣性力を数学的に計算してコリオリ力と遠心力に分けることはできますが，これらは一緒にはたらくので，実験的に分けて測定することは困難です． たとえば，回転する円盤上で球を転がして円盤に対する運動を調べるという実験では，物体の運動はコリオリ力と遠心力の両方の影響を受けることになるので，実験結果からコリオリ力だけを分けて考察するのはほとんど不可能だと思います．

ｋｏｍａｇａｔａｋｅさんの考察は興味深いものがありますが，いろいろな問題点も見受けられるように思います．

>中心からの半径方向の距離は一定の割合で増加していきます．円周上を回転方向とは逆にずれていきます．ズレの大きさは１，４，９，と増えていきますから等加速度運動に対応します．円周に沿っ方向に重力が働いている放物運動のようなイメージですね．円周に沿った方向に加速されているように見えるから対応する力を考えたのがコリオリ力です．中心からの距離が増えていくので一定の角速度で回転していても円周に沿った方向での移動距離が加速度的に変化するのです．コリオリ力の説明の場面です．

この説明からは，回転座標系で円周方向にはたらく見かけの力がコリオリ力であるように読み取れるのですが，一般にコリオリ力というのは（回転座標系での）速度に垂直にはたらく力であって円周方向だけにはたらくわけではありません． つまりコリオリ力は一般には円周方向と半径方向の両方の成分を持ちます． また，等速円運動の場合は，円周方向の移動距離の加速度的変化がないので，この説明によればコリオリ力ははたらいていないことになりますが，実際ははたらいています．

>中心からの距離の変化は加速度的ではありません．対応する力を考える必要はありません．

これも等速円運動の場合を考えると，中心からの距離の変化は加速度的ではありませんが，加速度はあります．実際，平面極座標での半径方向の加速度成分は 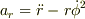なので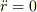， であっても 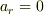ではありません． 当然この加速度に対応する力すなわち向心力もはたらきます．ただし，回転座標系の場合は本物の力ではなく，慣性力が（見かけの）向心力になることもあります．

>遠心力は円盤と一緒に運動している物体に対して働いているとしている力です．円運動は加速度運動であるのに観測者の立場から静止系に読み直しています．静止だから釣合の力が必要になります．この力の大きさは質量×向心加速度と同じになりますが意味が違います．

円盤と一緒に運動している物体にはたらく遠心力の説明としてはこれでいいと思います．しかし遠心力はこのような場合に限定されるものではありません． 一般に，遠心力は回転座標系ではたらく慣性力の１つであり，半径に比例した大きさで半径方向にはたらくものです．これは物体の運動状態には無関係にはたらきます．静止していても動いていても，円運動していてもしていなくてもはたらきます． また，向心力の有無にも関係なくはたらきます．

>釣り合いが破れて飛び出していったときの運動を遠心力による運動と見たくなるかも知れませんが運動方程式の中に入ってくる力にはなれません．

慣性系で考える場合はその通りですが，非慣性系である回転座標系で考える場合は遠心力とコリオリ力による運動と見なせます．もちろん，これらは本当の力ではありませんが，（回転座標系での）運動方程式の中には入ってきます．

>何かの事情で物体が中心からある距離離れたところで止まっているとします．その時は回転する円盤の上から見れば回転の方向と逆向きに等速で円運動していることになります．

その通りですね．等速円運動ですから向心力がはたらいていることになりますが，遠心力とコリオリ力の合力が向心力になっています．この場合,遠心力は中心から遠ざかる向きにはたらきますが，その遠心力の２倍の大きさのコリオリ力が中心に向かってはたらくので，合力が中心に向かう向心力になるわけです． もちろん本当の向心力ではなく，見かけの向心力ですが・・・．

なお，回転座標系での慣性力についての議論が過去ログにあります．参考までに

• http://hooktail.maxwell.jp/bbslog/9048.html

SATA_YUKI さんのレス (2006/09/04(Mon) 17:19)

yama様， komagatake様ありがとうございます． yama様へお伺いさせていただきたいことがあります．『コリオリ力だけなら，等速円運動になる』とあります．円運動するためには中心に向かってa = rω^2 の加速度が必要だと思うのですが，コリオリ力の加速度は a = 2vω ですが，円運動になるのでしょうか？ もし宜しければ，教えていただければと思います．もう少しで理解できそうです．

yama さんのレス (2006/09/04(Mon) 23:45)

等速円運動の向心力は，常に一平面上にあって，一定の大きさで，速度に垂直にはたらいていることはご存じのことと思います． 同様に，コリオリ力も常に一平面上にあって，一定の大きさで，速度に垂直にはたらきます．つまり，向心力と同じようにはたらくので，その結果，物体が等速円運動をすることが推察されると思います． 実際，きちんと計算すれば，等速円運動になることを示すことができます． ただし，その円運動の角速度は ω ではなく 2ω になります．つまり座標系（円盤）の回転の角速度の２倍になるわけです．また，円の半径は r=v/(2ω) となり，向心加速度 a = r(2ω)^2 は，コリオリ力による加速度 a = 2vω に一致します． 円運動の角速度が 2ω になるのは奇妙に思われるでしょうが，これはあくまでもコリオリ力だけがはたらくと仮定した場合のことであって，実際に角速度 2ω の等速円運動になるわけではありません． つまり，コリオリ力だけがはたらくことは実際にはありえず，必ず遠心力も一緒にはたらくということです． ただし，本当の力がはたらく運動では，コリオリ力が遠心力に比べて非常に大きくなることも多く，その場合は近似的に遠心力を無視することができます．

SATA_YUKI さんのレス (2006/09/05(Tue) 09:46)

yama様ご丁寧なご説明ありがとうございます．『回転する円盤状で中心から外に向かって等速直線運動をする物体を観察した時に，その物体が等速直線運動ではなく，円盤の回転方向とは逆ににズレていくように見える』現象について，わかってきたような気がします． そこで，yama様のご説明を受けて，確認させていただければと思います． 『回転する円盤状で中心から外に向かって等速直線運動をする物体を観察した時に，その物体が等速直線運動ではなく，円盤の回転方向とは逆ににズレていくように見える』のは遠心力とコリオリ力が働くためである．そして， コリオリ力は 2vω と常に一定の大きさである．（この場合の v は回転する円盤の中心から外に向かって運動している物体の速度）・・・（１） 遠心力は rω^2 = vω であり，その大きさは時間経過とともに大きくなる． （この v の半径方向成分の速度変化は一定であるが，円周方向成分への速度変化が大きくなるので，結果的に v の速度は大きくなる）・・・（２） （１）（２）から，「回転する円盤状で中心から外に向かって等速直線運動をする物体を観察した時に，見かけ上の力である遠心力とコリオリ力が働き，遠心力＞コリオリ力となるために，その物体は等速円運動ではなく，半径方向へ物体が運動しているように見える」という理解で宜しいのでしょうか？ もしかすると，yama様の説明を受けてもなお，おかしな解釈をしているかもしれませんが，もし宜しければ確認させていただければと思います．どうぞ宜しくお願い致します．

ｙama さんのレス (2006/09/05(Tue) 17:32)

図を書いてみると，物体は渦を巻きながら中心からだんだん遠ざかるような運動をすることがわかりますね．この運動の経路は数学でアルキメデスの螺旋といわれるものです．

この運動はコリオリ力と遠心力がはたらくと考えて説明することができます． コリオリ力の大きさを 2mvω と表すときの v は，回転座標系での物体の速さです． つまり，半径方向の速度成分だけでなく，円周方向の速度成分も含めた速さです． 半径方向の速度成分v0は一定ですが，円周方向の速度成分 -rω=-v0ωt が変化するため，v は一定ではなくだんだん増加していきます． コリオリ力は速度に垂直なので，円周方向の速度成分によってコリオリ力の半径方向の成分が決まり，半径方向の速度成分によってコリオリ力の円周方向の成分が決まります．その結果，コリオリ力の半径方向の成分は -2mv0ω^2t，円周方向の成分は -2mv0ω になります． また，遠心力は半径方向の成分だけを持ち mrω^2=mv0ω^2t になります．mvω ではありません． 従って慣性力全体としては半径方向に -mv0ω^2t，円周方向に-2mv0ω となります． 半径方向の成分は -mrω^2 と表すこともできますが，これは等速円運動の向心力と同じです．等速円運動の場合は r が一定ですが，半径方向の加速度が -rω^2 であることは必ずしも r が一定であることを意味せず，一般には dr/dt が一定になります．この運動でも，確かに dr/dt=v0=一定 です． ω が一定なので r が変化すると円周方向の速度成分 -rω も変化します．従って円周方向の加速度成分がなければなりませんが，コリオリ力の円周方向の成分によって，それが生じるわけです．

従って「遠心力＞コリオリ力となるために，その物体は等速円運動ではなく，半径方向へ物体が運動しているように見える」と考えるのは間違いです． コリオリ力の半径方向の成分は遠心力の２倍です．その結果 dr/dt が一定に保たれるので，初めに中心から遠ざかる向きに動き出した物体は，同じ速さ（半径方向の速度成分）で遠ざかり続けるのです． 同時に，コリオリ力の円周方向の成分のために円周方向の速度成分は増加していきます．

「遠心力＞コリオリ力」であるという誤解は，「中心から遠ざかる運動をしているのだから中心から遠ざかる向きに力がはたらいているはずだ．」と考えるためではないでしょうか．これが間違っていることは，慣性系で考えてみれば分かります．慣性系では，物体は中心から遠ざかるような等速直線運動をしますが，中心から遠ざかる向きに力がはたらいているわけではありません．力がはたらかないため初速度を保ったまま動き続けるわけです．回転座標系の場合は，等速直線運動ではなく周回しながら遠ざかっていくため，中心に向かう慣性力がはたらくことになります．

一応このように説明できますが，もともとは慣性系で等速直線運動をしているわけなので，慣性系で考えれば何も難しい説明は必要ないわけです． それを，非慣性系で説明するためにコリオリ力や遠心力を導入するわけで，それによってもっともらしく説明はできますが，こじつけのようにも思えますね.

komagatake さんのレス (2006/09/06(Wed) 10:00)

ｙａｍａ様おはようございます．ｋｏｍａｇａｔａｋｅです．

最初に私があのように書いたのは座標系を変換するとどうして力が生じるかをわかりやすく示したいと思ったからです．加速度の生じるところを示せば力が生じることは理解しやすくなります．相対運動は式の変換だけでなかなかわかりません．ピンと来ないのです．等速度運動をしている２つの系の間でも難しいです．私は授業でも全て一定時間毎の位置を書いて説明してきました．一旦イメージが取れたら式で考えていくことも出来ます．

静止系と回転系の変換はしんどいです．イメージが取りにくいです．高校の物理では殆ど扱いませんので正面からやった経験があまりありませんでした．地学では出てきます．でも当然結果だけです．皆そうかなと思っているだけです．

今回はいい機会になりました．ｙａｍａ様が参考に上げられた過去ログを見て計算しました．ちょっと時間がかかりました．でもどういう仕組みになっているかは理解できたように思います．理解した範囲のことを書かせていただきます．

ｘ，ｙ直角座標をｒ，θの極座標に変換します．静止系で中心を通る等速直線運動（速さｖ）を回転系（角速度ω：一定）で見たときにどう見えるか．これは難しくありません．ｒ＝ｖｔ，θ＝−ωｔです．これを私は半径方向に一定の速さ，円周に沿っては加速度的と表しました．「的」という言葉を使ったのは円運動自体が加速度を持つので円周の長さだけについてみたらという区別のためです．これはイメージを取るためです． 回転系から見たこの運動は絶えず方向が変化していますから力が働いていることになります．この力はこの回転系での加速度を求めれば求まります．極座標表示での速度と加速度は次のようになります． 速度：（ｒ’，ｒθ’）＝（ｖ，−ｒω），速さ：Ｖ＝√（ｖ＾２＋（ｒω）＾２） 加速度：（ｒ’’−ｒθ’＾２，２ｒ’θ’＋ｒθ’’）＝（−ｒω＾２，−２ｖω） ※（，）の中は前が半径方向，後ろが角度方向です．「’」は時間微分です．

力はこの加速度に質量をかけたものになります．

ここまでは座標変換だけのことです．回転系での物体の運動を見たとき方向が変わっているのはこの力全体の働きです．これで初めて静止系から見た運動と対応がつきます．この力から「コリオリ力」と言われているものを抜き出すかどうかとも無関係なはずです．「転向力」と言っていいでしょう．この力（加速度）は速度と垂直ではありません．２つのベクトルの内積がゼロでないことからすぐにわかります．

私が最初に書いた時の表現で言うと円周に沿っての距離の変化に対応する加速度が−２ｖωです．これは（ａｔ＾２）／２＝ｒθ＝−ｖωｔ＾２から出すことも出来ます．これが上の加速度の表現の中にも出ています．でもここでのｖは元の静止座標系で見たときの物体の速さです．今は回転系で見ています．速さＶで運動している物体に働いている力ですからＶを使った表現になっていないと具合が悪いです．そこで大きさが２Ｖωで，かつ速度に垂直な加速度を抜き出します．（「抜き出す」のであって成分に分解するのではないところが巧妙です．私は初め直角成分に分解していてこんがらがりました．） この加速度は２ω（−ｒω，−ｖ）です．−は元の加速度の働いている側としたので出てきたものです．抜き出せばおつりが出てきます．おつりに対応する加速度は加速度ベクトルの引き算をすれば求めることが出来ます． （−ｒω＾２，−２ｖω）−２ω（−ｒω，−ｖ）＝（ｒω＾２，０） このおつりの加速度は半径方向に向いていて大きさがｒω＾２です．これをｙａｍａ様は「遠心力」と呼んでいます．加速度運動から出した力ですから回転系で実際に働いている力です．この力がなければｒが大きくなれません．運動方程式の中に入ってくる力です．名前と表現は静止系での等速円運動を回転系で見たときに出てくるものと同じですが意味は違っています．区別する必要があります．速度に垂直な力だけでは円運動しかできませんから元々の「中心から遠ざかる運動」を表すためにはこれが必要になります．このおつりは半径の方向です．運動の方向ではありません．だからこの力はｒを変化させますが向きも変えます．

ここでこの「速度に垂直な大きさ２Ｖωの力」を「コリオリ力」とｙａｍａ様は呼んでいます．とすると「コリオリ力」は物体が方向を変えていく運動の原因の一部です．あくまで方向を変えているのは力の全体（上で私が「転向力」と呼んだもの）なんですからそう言うことができます．抜き出した一部の力で運動の全体を記述することは出来ないことになります．コリオリ力の円周方向成分という表現も用いておられますが元々力は半径方向と円周方向とで表されていましたからそこの表現に戻っただけの話です．

参考にと挙げていただいた過去ログの中に「向心力」という表現がありました．トンガリ様です．ｙａｍａ様はそれを否定していました．運動を記述すると言うだけであれば間違いではありません．働いている力を半径方向の成分と角度方向の成分とに分けて考えるという立場であれば中心に向かってｒω＾２の大きさの力が働いていますから「向心力」です．半径方向には２ｖωです．曖昧さはありません．互いに垂直な２つの成分ですから働きもはっきりしています．ただこの角度方向の力を「コリオリの力」と呼ぶのには問題があるということです．ベクトルは任意の２つの方向に分解できます．半径方向と速度に垂直な方向の２つに分解したときにｙａｍａ様の言う「コリオリ力」が出てきます．その時はもう一つが「遠心力」になります．トンガリ様の「向心力」とｙａｍａ様の「遠心力」は対等です．同じ力を２つに分けるその方向が異なるのですから．運動の記述という面では同等です．気象学で言う「コリオリ力」に対応させようという方向があるから違いが出てきます．

はじめの質問に戻ります．静止系で等速直線運動をしている物体の運動を回転座標系で見ても円運動にはなりません．これは当然です．もし円運動になっていれば座標変換にどこか誤りがあるのです．だから逆に座標変換でのミスのチェックに使うことの出来るものです．これはコリオリ力をどう考えるかとも無関係です．

気象学の入門書やインターネットのサイトでは「転向力」を速度に垂直だとして矢印を入れています．圧力勾配に伴う「気圧傾度力」と釣り合うと「地衡風」になると書いてあります．力はこの２つしか書いてありませんからここで求めたものと食い違います．「転向力」の中身は「コリオリ力」であるとしている記述もあります．「コリオリ力」を速度に垂直な力と見ているのであればおつりがあるはずですから図の中には力が３つ必要になるはずです．摩擦を入れれば４つ矢印がいるはずです．

気象学の方ではコリオリ力を実際のところどう扱っているのでしょうか．きちんと導いているのでしょうか．または異なるモデルで導いているのでしょうか．モデルによって結果が違うのでしょうか．

静止系では中心を通る等速円運動であるとしました．その限りではここで導いたように割合とすっきりとした簡単な表現になります．中心からｄ離れたところを通過する等速直線運動でも同じ内容のものが得られるのでしょうか．試みてみましたが結果からすっきりとしたものを抜き出すことが出来ませんでした．成功されている方がおられれば教えていただきたいと思います．

SATA_YUKI さんのレス (2006/09/06(Wed) 12:35)

yama様ご丁寧なご説明誠にありがとうございました． 学生の時に少しだけコリオリ力に触れその時には深く考えませんでしたので，何の疑問も持ちませんでした．最近自然現象の原理・法則について興味があり，改めて詳しく考察しようとした時に戸惑ってしまいました．今後も自分なりに自然現象の原理・法則について理解を深めていけたらと思っております．今後とも宜しくお願い致します．

ｙama さんのレス (2006/09/06(Wed) 14:27)

ｋｏｍａｇａｔａｋｅ様，詳しい御考察ありがとうございます． 一部の記号が異なるところがありますが，私が書いた式で v を V，v0 を v で置き換えればｋｏｍａｇａｔａｋｅ様が導かれた結果と一致しています． しかし,用語の定義が違っているようですね． 私が「慣性力全体」とよんでいるものをｋｏｍａｇａｔａｋｅ様は「転向力」とよばれているようです． また，私の用語では

慣性力（全体）＝コリオリ力＋遠心力

となり，ｋｏｍａｇａｔａｋｅさんの用語では

転向力＝速度に垂直な大きさ２Ｖωの力＋おつり

となると思います．これは用語は違いますが，内容は同じだと思います．

私は，力学の教科書などで一般的に用いられる意味に用語を用いています． 力学の教科書によると回転座標系での運動方程式は次のようになります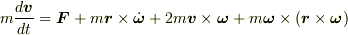． ここで，右辺の第２項は回転の非一様性による力，第３項はコリオリ力，第４項は遠心力で，これら全体が回転による慣性力であるとされています． 式からわかるように第３項は速度に垂直な大きさ2mvωの力であり，第４項は回転軸に垂直で軸から遠ざかる向きをもち，大きさ mrω^2 の力です．（r は回転軸からの距離です．）

また「転向力」については，私が知る限り，「コリオリ力」と同じ意味に用いられていて，「慣性力（全体）」の意味に用いられている例はありません．「この力を転向力（またはコリオリ力）という．」のような記述もよく見られます． 物理関係の本では「コリオリ力」，地学関係の本では「転向力」が用いられることが多いようです．

地衡風の場合に遠心力（ｋｏｍａｇａｔａｋｅ様のいわれる「おつり」）を考えないのは，遠心力が重力に繰り込まれているからです．つまり，地球上での重力は，自転による遠心力と万有引力の合力です．地衡風の場合，普通は重力は考えないし，まして重力に繰り込まれている遠心力だけを引き出して考える必要はまずありません．

今回の例に限っていえば，慣性力を１つにまとめて扱ったほうが簡単で，コリオリ力と遠心力に分けることはかえって不自然で煩雑であるようにも見えます． しかし，もっと一般の場合を考えると，この分け方が自然であることが分かります． たとえば，回転する平面上の物体の運動方程式は，コリオリ力と遠心力を考えると次のようになることが容易に分かります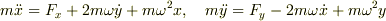． それぞれ，第２項がコリオリ力，第３項が遠心力を表しています．

SATA_YUKI さんのレス (2006/09/06(Wed) 16:11)

komagatake様・yama様本当にありがとうございます． yama様は『ω が一定なので r が変化すると円周方向の速度成分 -rω も変化します．従って円周方向の加速度成分がなければなりませんが，コリオリ力の円周方向の成分によって，それが生じるわけです．』と書いており，理解できます．しかし，式から理解しようとした場合に理解できません．と申しますのは 円周方向の速度成分は -v0ωt より，円周方向の速度成分の変化量（加速度）は v0ω ですよね．・・・（１） また，コリオリ力の円周方向の加速度成分は -2v0ω ですよね．・・・（２） （１）（２）が一致しないんです．なぜ，ですか？ 本当に申し訳ございませんが，教えていただければと思います．

ｙama さんのレス (2006/09/06(Wed) 17:00)

「向心力」についてですが，私はトンガリさんの，【向心力】を全面的に否定しているわけではありません．私自身もこのスレでは「（見かけの）向心力」という言葉を用いました．

>回転座標系での慣性力を，【向心力】と【コリオリの力の一例】としている点は疑問です．【向心力】と【コリオリの力の一部】とすれば辻褄は合うと思いますが，それでも一般的な定式化とは異なっているので，混乱を引き起こすおそれがあります．つまり，回転座標系での慣性力は，一般的には遠心力とコリオリの力に分けて考えますが，あなたの定式化では，遠心力が見かけ上消えてしまっているからです．

と書いているように，【向心力】というものを慣性力として導入することは，一般的な定式化とは異なっているので混乱を引き起こすおそれがあるといっているわけです． 慣性力の半径方向の成分は，中心に向かうので，見かけの上では向心力とみなせるということを否定しているわけではありません． 慣性力をコリオリ力と遠心力に分けて考えるのが一般的な定式化だと思います．遠心力を考えないで【向心力】を考えるのは一般的ではありません．

また，遠心力を考えない場合は，次のようなおかしなことになります． 円盤の中心軸につないだばねに物体をとりつけてから，円盤を回転させます． 回転するとばねが伸びます．慣性系から見るとばねの力が（本物の）向心力となって物体は円運動します． これを円盤上で観察するとばねの力がはたらいているのに物体は静止しています． 従ってばねの力とつりあうように，中心と反対向きに慣性力がはたらいていると考えなければいけません． この慣性力はどう説明されるでしょうか．トンガリさんやｋｏｍａｇａｔａｋｅさんは，円周方向の慣性力をコリオリ力とされていますが，この力は半径方向の力なのでコリオリ力ではありません．（通常の定義によっても，静止している物体にはコリオリ力ははたらきません．） また，この力は中心に向かわないので【向心力】ではありません． 【向心力】の定義を広げて，逆向きの場合も【向心力】と考えればいいかもしれません． しかし，そうすると【向心力】は中心に向かう場合も，その反対に向かう場合もあることになります．ではその向きはどのように決まるのでしょうか． 向きを決める法則があるとしても，かなりわかりにくいものになり，すっきりしたものにはならないと思います．

これに対して，通常の定式化では，この慣性力は遠心力と考えます． 遠心力は常に半径方向で，中心から遠ざかる向きに向かい，逆向きにはなりません． また，もう１つの慣性力はコリオリ力で常に速度に垂直にはたらきます． これらを合成した力の半径方向の成分が中心に向かう場合，それは向心力のように見えます．しかし，この「（見かけの）向心力」は，遠心力とコリオリ力から導かれる派生的な力であって，基本となる慣性力は遠心力とコリオリ力の２つであると考えたほうが，慣性力の定式化としてはすっきりしていると思います.

SATA_YUKI さんのレス (2006/09/06(Wed) 17:05)

yama様は『ω が一定なので r が変化すると円周方向の速度成分 -rω も変化します．従って円周方向の加速度成分がなければなりませんが，コリオリ力の円周方向の成分によって，それが生じるわけです．』と書いており，理解できます．しかし，式から理解しようとした場合に理解できません．と申しますのは 円周方向の速度成分は -v0ωt より，円周方向の速度成分の変化量（加速度）は -v0ω ですよね．・・・（１） また，コリオリ力の円周方向の加速度成分は -2v0ω ですよね．・・・（２） （１）（２）が一致しないんです．なぜですか？ 本当に申し訳ございませんが，教えていただければと思います．

ｙama さんのレス (2006/09/06(Wed) 17:18)

>円周方向の速度成分は -v0ωt より，円周方向の速度成分の変化量（加速度）は v0ω ですよね．・・・（１）

円周方向の加速度は，速度成分を単純に時間で微分したものではありません． 面積速度（の２倍）を時間で微分して，それを r で割ったものになります． すなわち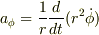， です．

komagatake さんのレス (2006/09/06(Wed) 18:09)

ｙａｍａ様

中心からｄ離れたところを速さｖで通過する等速度運動の場合にも同じような表現を得ることが出来ました．速度に垂直で大きさが２Ｖωの加速度，おつりは半径方向にｒω＾２です．ちょっとややこしかったです． これで区切りがつきました．

SATA_YUKI さんのレス (2006/09/06(Wed) 18:40)

yama様へ本当にありがとうございます． yama様のご説明文にある「コリオリ力の半径方向の成分は遠心力の２倍です．」はわかるのですが，「その結果 dr/dt が一定に保たれる」ということがわかりません． この点について教えていただきたいです． また，円周方向の加速度成分を求めるときに，なぜ単純に円周方向の速度成分を微分することでは求められず，面積速度という考え方をするのですか？ yama様にとりましては基礎的基本的なことかもございませんが，物理学の理解の程度が高校レベルの私にとっては新しい気付きの連続となっており，理解していくことが楽しいです． ぜひ，上記２点について教えていただければと思います．どうぞ，よろしくお願い致します．

yama さんのレス (2006/09/06(Wed) 18:57)

極座標での加速度について解説したサイトはいろいろあります．たとえば

• http://www14.plala.or.jp/phys/tools/9.html

などです．

r方向の加速度の式を用いれば dr/dt が一定になることが導けます． すなわち，運動方程式が 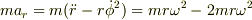となるので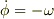， を用いると 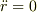が導かれます．これは 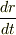が一定であるということです．

yama さんのレス (2006/09/06(Wed) 23:10)

ｋｏｍａｇａｔａｋｅ様 ややこしい計算お疲れさまでした．

>中心からｄ離れたところを速さｖで通過する等速度運動の場合にも同じような表現を得ることが出来ました．速度に垂直で大きさが２Ｖωの加速度，おつりは半径方向にｒω＾２です．

２種類の加速度のうち，前者は速度に関係して位置に無関係，後者は位置に関係して速度に無関係ですね．従って，加速度をこの２種類に分けることは，ごく自然なことだと思えます． 普通は，前者に対応する力がコリオリ力，後者（おつり）に対応する力が遠心力といわれるようですが・・・．

SATA_YUKI さんのレス (2006/09/07(Thu) 01:09)

yama様及びkomagatake様へ 本当にお世話になりました．お陰様で何とか理解することができました． 自分なりにこれからも自然科学を探求していきたいと思います． どうぞ宜しくお願い致します．

yama さんのレス (2006/09/07(Thu) 07:20)

頑張ってください．

なんとなく さんのレス (2006/09/07(Thu) 08:32)

>yamaさん

なんとなくです．重箱の隅ですが， NO.11730の最後の２式，遠心力部分にｍが抜けていませんか．

ｙama さんのレス (2006/09/07(Thu) 08:51)

ご指摘ありがとうございます． 確かに抜けていましたね．符号も間違っていました． いずれも訂正しておきました．

通りすがり さんのレス (2006/09/07(Thu) 10:15)

yamaさんへ NO.11730の最後の２式でコリオリ力を表す式の符号が異なっているのですが，同じになるのでは？

通りすがり さんのレス (2006/09/07(Thu) 10:53)

yamaさんへ 大変失礼致しました．yamaさんの通りでした．申し訳ございませんでした．

komagatake さんのレス (2006/09/09(Sat) 11:36)

ｙａｍａ様

おはようございます．ｋｏｍａｇａｔａｋｅです．

コリオリ力や遠心力は回転する座標系に移って運動を記述するときに現れる一般的な力であるということでした．その時の運動方程式を示していただきました．

はるか過去の記憶の中にあった式です．数式的な変換の中だけで終わってしまっていて実感のレベルまで降りてこないままに忘れてしまっていました．今改めて力学の本を読み直してみようと思っています．ベクトル積の出てくる力学なんて本当に久しぶりです．３０年以上間があいているでしょう．

あちこちに考え違いがあったようで恥ずかしい気持ちになっています．

高等学校の物理の教科書では慣性力に触れないという立場です．これについて私の理解しているところを描かせていただきます．

それは運動方程式で考えるという方向に合わないからです．運動を解析していくときにどこに力が働いているか，その力はどの様な加速度を生じているかを吟味していきます．これは意外と難しい作業です．２つの物体が関係するときなど急に難しくなります．着目している物体と力との対応が難しくなるからです．Ａの運動を考えているときにＢに働いている力を持ち込んではいけないというのはなかなか出来るようにはなりません．円運動の場合，加速度運動であるというのが一つのネックになっています．でもこの加速度があるからこそ，中心向けの力が必要になるのです．どの様な力かは場面によって変わるだろうがとにかく力が必要だ，紐の張力の場合もあれば，壁からの抗力の場合もある．太陽，地球の間に働く万有引力もその一つだという流れです．全ての場合で一貫して「力は？」とか「加速度は？」と確かめていかなければ出来るようにならないのです．ところが「遠心力」という言葉が使われているときはその加速度を意識していません．釣合に話を持ち込みます．回転する座標系に乗って見ているという意識はあまりありません．極端に言えば回転座標系の言葉を使っているのに静止座標系で見ているのです．式が簡単になるからです．円運動の加速度を考える必要がなくなりますので中学校でも使っているようです．「糸につながれた物体が水平面内で等速円運動をしている．この糸が切れたときに物体が飛び出していく方向は？」という問題では過半数の生徒が「接線方向」と答えることが出来ない状態です．センターレベルでの入試問題に出ることもあります．これが簡単であれば入試に出ません．間違う生徒が多いから出るのです．釣り合っている力の片方がなくなれば残りの力の方向に運動し始めると考えるからです．どの立場で見ているのかも混乱しています．

回転座標系に乗れば簡単になる問題もありますがかえって複雑になるものもあります．ここの欄での最初の質問では等速直線運動がややこしい加速度運動になっています．座標が静止しているときの運動方程式はｍａ＝Ｆです．いくつかの力が働いていて釣り合っているとき（Ｆ＝０のとき）ａ＝０です．その力の一つが変化してＦが０なくなったときはその新しい力で運動が始まります．回転座標系で遠心力が働いていて釣り合っている時をこれと同じように考えてしまうのだと思います．物体をつないでいる糸が切れたときは遠心力だけで飛び出していくと考えてしまうことになります．「一緒に回転している人から見たら半径方向に飛び出していくが静止系で見たらどうなる？」というような座標系の意識もありませんからそのまま中心から遠ざかる方向に答えを考えてしまいます．回転座標系ではｍａ＝Ｆではなく，ｍａ＝Ｆ＋コリオリ力＋遠心力だということが抜けています．でも元々が円運動での加速度を避けて釣合に持ち込んだのですから当然この様なややこしい式は意識されていません．

※「水平面内で円運動をしている振り子の糸が切れた後の物体の運動を回転座標系で表現する」というのは「中心からｄ離れたところを等速度で通過する物体の運動を回転座標系で記述する」というのと同じですね．

「慣性力」という言葉も混乱して使われています．ＴＶのクイズ番組等で「物体には同じ運動を続けようとする性質があります．これを慣性の法則といいます．だから物体には慣性の力が働いています．・・・」とか「物体には横向けに慣性の力が働いています．下向きには重力が働いています」とかいろいろです．ＴＶ番組にもアドバイザーがついているはずですからこれは司会者の言葉ではありません．アドバイザーの発言だと思います．昔の「勢い理論」に戻っています．小中学生向きの本にも出てきます．専門的に「慣性力」という言葉がある事がこういう使い方の支えになっているようにも思います．ＴＶで使われていますから生徒も使います．授業で修正するのに苦労します．でも生徒はこれは授業の中だけのことで世間的にはＴＶの方が通用すると思っている可能性が大きいです．

ＳＡＴＡＹＵＫＩ様へ

この歳になって力学の教科書を見直そうと思っています． ＹＵＫＩ様は若いと思います．しっかりしたｔｅｘｔを見つけて勉強していくことが出来ると思います．

頑張って下さい．

yama さんのレス (2006/09/09(Sat) 15:03)

以前は高校物理でも電車が加速するときの慣性力が取り扱われたり，遠心力も慣性力の一種として取り扱われていたこともありましたね．その場合もコリオリ力は扱われませんでした．コリオリ力は地学で（一時は理科?でも）扱われていましたし現在も扱われていますが，物理で扱う慣性力との関連にはほとんど触れられなかったと思います． しかし，これらの内容が，当時の生徒達にきちんと理解されていたかというとそれは疑問ですね．このあたりの事情はｋｏｍａｇａｔａｋｅ様は十分ご存じのことと思います．

現在の高校物理では慣性力はほとんど扱われていませんが，これについてはｋｏｍａｇａｔａｋｅ様の見解が当たっていると思います．． 中途半端な理解では，いろいろな誤解や混乱を招くおそれがあるので，非慣性系を考えないで，すべての運動を慣性系だけで考えれば，取り扱いはすっきりしたものになります．

しかし，一方では，遠心力という言葉が日常語として普通に用いられています．ただし，ｋｏｍａｇａｔａｋｅ様が書かれている通り正しく理解されてはいないようですが． また，自動車が加速・減速するときの慣性力や，カーブを曲がるときの遠心力は我々の日常感覚に深く結びついています．これを慣性力を導入しないで慣性系の立場だけで説明することも可能ですが，感覚的な認識からずれるように思います．

このような事情を考えると慣性力を完全に排除してしまうことにはちょっと疑問を感じます．しかし，取り扱うとしてもどのように取り扱うのが適切であるかは難しい問題ですね．