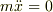ペン さんの書込 (2006/04/09(Sun) 01:03)

こんばんは．非慣性座標が苦手で全く手のつけられない問題があったのでよろしくお願いします．問題集もしらべたのですが，この手の問題はあまり載ってませんでした（重要度は低いのでしょうか？）．

水平に置かれた滑らかなターンテーブルが垂直な軸のまわりに一定の角速度ωで回転している．質量ｍの質点が時刻ｔ＝０に回転軸からターンテーブル上面に沿って速さｖで打ち出された．その後，質点は慣性座標系から見て等速度で運動する．ターンテーブルに固定した座標からみて質点がどうなるか，次の問いに答えよ． 1，質点の軌道を求めよ．

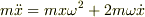
とりあえず運動方程式を書いて，x，yを求めて，ｔを消去しようと思いました． ですが，この微分方程式を解くことが出来ませんでした． それと，疑問なのですが，なぜ遠心力がかかるのでしょうか？ 回転している座標系からみると，コリオリ力はイメージできるのですが，ｘ方向に 引っ張られるイメージが湧きません．そのままx方向には等速度運動をするように感じられます．

ペン さんのレス (2006/04/09(Sun) 02:56)

上の式のほうはx＝e^(λt)を代入したらx=(v0/ω2√2){e^((1+√2)ωt)-e^((1+√2)ωt)}という複雑な式になってしまいました． 下のほうはdy/dt=Ce^(-2ωt)まで出来たのですが，初期条件を代入するとｙ＝０になってしまいました．

ペン さんのレス (2006/04/09(Sun) 03:03)

すみません！完全な勘違いでした． コリオリの力のｘ，ｙは逆ですね．しかし，互いの式にｘ，ｙが入ってるなんてどうやって解けばいいんでしょうか・・・？

yama さんのレス (2006/04/09(Sun) 09:46)

この場合は，回転座標系で運動方程式を考えるとかえって難しくなると思います． 慣性座標系での等速度運動の式は簡単に表されるので，それを座標変換によって回転座標系での式に書き直せばいいと思います．

ペン さんのレス (2006/04/09(Sun) 15:14)

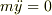慣性系ではこうですよね？ これを各成分にわけた状態のまま，座標変換するということでしょうか？どのようにすればよいのかわからないです・・・．

yama さんのレス (2006/04/09(Sun) 16:44)

慣性座標系で初速度の向きにX軸をとると x＝vt y＝0 と表せるので，これを座標変換して回転座標系での式に書き直すということです．

ペン さんのレス (2006/04/09(Sun) 17:22)

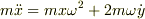
座標変換というのは，(vt)i+(0)j=x'i'+y'j'を２階微分するというやりかたですよね？ 結局 になるのですが．別の方法ということですか？ なんどもすみません．

yama さんのレス (2006/04/09(Sun) 17:43)

座標系を角度ωtだけ回転させればいいので x'＝xcosωt＋ysinωt y'＝-xsinωt＋ysinωt です．これにx＝vt, y＝0 を代入します． 運動方程式を書くのではなく，初めから運動方程式を解いた式を考えるわけです．

ペン さんのレス (2006/04/09(Sun) 21:04)

なるほど・・・．その発想はありませんでした． ところで，もともと座標系を選ぶのは運動の記述を簡単にするためですよね？ なぜ，余計むずかしくなる座標系に直すのでしょうか？問題で問われてるからってだけの理由でしょうが・・・． それと，9056にかいた運動方程式を解くのは不可能ですか？

yama さんのレス (2006/04/09(Sun) 23:05)

>ところで，もともと座標系を選ぶのは運動の記述を簡単にするためですよね？ >なぜ，余計むずかしくなる座標系に直すのでしょうか？問題で問われてるからってだけの理由でしょうが・・・．

我々は回転する地球上にいるので，地球上の物体の運動を観測結果と比較して考察するには非慣性系を用いる必要があります． この問題の場合は慣性系で考えたほうが式が簡単になりますが，非慣性系で運動方程式を考えたほうが都合がよい場合もあります．

＞それと，9056にかいた運動方程式を解くのは不可能ですか？

この方程式には間違いがあり，y成分の式にも遠心力が必要です． 正しい運動方程式をつくれば，それを解くことは可能であり，それは当然，慣性系で解いた式を座標変換したものに一致するはずです． 答が分かっているのだから，その答がうまく導かれるように途中の過程を考えてみてはいかがでしょうか．

ペン さんのレス (2006/04/09(Sun) 23:31)

ありがとうございました．じぶんで研究してみます．

それと，一番最初にも書いたのですが，この場合の遠心力の原因は何なのでしょうか？ 僕は，回転軸からみると物体が静止して見えるので，運動の法則に矛盾しないように向心力と逆向きの力を考えなければいけないため，と理解していたのですが， この問題の場合は向心力がないですよね？

yama さんのレス (2006/04/09(Sun) 23:58)

遠心力と向心力は直接には関係ありません． 向心力は本物の力であり，どんな座標系においてもはたらきます． これに対して，遠心力は本物の力ではなく，回転座標系で生じる見かけの力であり，慣性系に移れば消えてしまいます． つまり，回転座標系への座標変換の結果，見かけの力として遠心力が生じるわけで，遠心力を及ぼすような物体があるわけではありません． 座標系の回転自体が遠心力の原因であるとも言えるでしょう．

なお，このあたりのことをさらに追究すれば，マッハの原理とか一般相対性理論とかが関係してきます．興味があれば調べてみてください．

ペン さんのレス (2006/04/10(Mon) 00:45)

座標変換によって出てきた見掛けの力，というのはもちろんわかっているんですが，もっと定性的な説明はできませんかね？ ありえないですけど，もし，僕がターンテーブルの上にいたら力を感じるわけですよね？(回ってることに気付かなければ何かに引っ張られてると思うはず)それはなぜなんでしょうか？ たとえば，電車が急停止したときに感じる慣性力の正体は，自分が慣性系では動き続けようとしているから，ですよね？

ｙama さんのレス (2006/04/10(Mon) 08:48)

遠心力もコリオリの力も慣性力の一種であり，物体が慣性系において等速直線運動を続けようとする性質によるものです． 慣性系での等速直線運動は，非慣性系では等速直線運動ではなく，もっと複雑な運動になりますが，非慣性系での観測者にはその複雑な運動をさせようとする力がはたらいているように見えるわけです． その見かけの力が遠心力やコリオリの力であって，それは向心力の有無には関係ありません．

ペン さんのレス (2006/04/10(Mon) 14:31)

遠心力もコリオリ力も慣性の法則が原因なのですか． 並進座標の慣性力のときに比べてイメージしづらいですね・・・． 疑問につきあってくださって，ありがとうございました．

やかん さんのレス (2006/04/10(Mon) 14:50)

ベンさん，はじめまして！yamaさん，こんにちは！

＞ありえないですけど，もし，僕がターンテーブルの上にいたら力を感じるわけですよね？(回ってることに気付かなければ何かに引っ張られてると思うはず)それはなぜなんでしょうか？

名前は知りませんが，遊園地なんかで，円盤がグルグル回って，円周上の柵に人が立った姿勢で押し付けられるやつ，なんかありますよね．答えというより解釈かもしれませんが，力を感じる人，眼，が回転座標系にいるにもかかわらず，いつもの静止座標系にいる気になっているから，数式通りに，遠心力の大きさの力を”感じる”のではないでしょうか？コリオリ力も，中華料理の円卓上にカメラを設置して，円卓を回転させてもカメラの見る床の景色は動かない，そこにボールを転がすと，あれっ，不思議にカーブする！それが円卓の外から見ていればなんという事はないのに，回転している円卓上をあたかも静止しているように考えちゃうから（見ちゃうから），差し引き，見かけの力を考えて，つじつまが合う（計算上も，感覚上も）という事でしょうか．エレベータも，カゴが動かないと思っているから，体が浮いたり重くなったりするような気がする？？変な事書いてすみません・・・． (^^;

ペン さんのレス (2006/04/10(Mon) 15:04)

ええ，まさに同じことを考えていました． 数式をいじっていったら，変な項がでてきて，しかもそれで感覚上のことが説明できたなんて，，，なんか不思議ですね． こんど公園にいって実験してみようかな(笑)

トンガリ さんのレス (2006/04/18(Tue) 21:18)

【慣性座標系から見た質点の軌道】 質量ｍの質点が時刻ｔ＝０に回転軸からターンテーブル上面に沿って速さｖで打ち出された． その後，質点は慣性座標系から見て等速度で運動する．

慣性座標系に回転軸を原点としｖの方向に延びるるＸ軸を準備しました． この時の運動方程式は簡単 Ｘ'＝ｖ で Ｙ'＝０ 微分方程式を解いた軌跡は Ｘ＝ｖｔ で Ｙ＝０

【ターンテーブル座標系から見た質点の軌道】 ターンテーブル座標系にＲ軸とΘ軸を準備しました． この時の運動方程式は簡単 Ｒ'＝ｖ で Θ'＝−ω 微分方程式を解いた軌跡は Ｒ＝ｖｔ で Θ＝−ωｔ

この軌跡の図形は，蚊取り線香状の渦巻きです． この図形は機械工学では回転運動を直線運動に変換する機構に応用されます． 例えば三つ爪チャックでは回転軸から１２０度おき３方に打ち出された３個の質点の軌跡の溝 を持つ円盤を回転させて，溝に配置した３個の爪を半径方向にのみ移動させて， 様々な太さの丸棒を正確に保持する装置になります．だだし電気ドリルのチャックは似て非です．

上記の三つ爪チャックの円盤に３個の溝を機械加工する古典的な方法は， 円盤を回転させながら溝を掘る刃具を半径方向に移動させることです． そんな構造の工作機械がありました．今は数値制御の機械が主流ですが．

＝ 追伸 ＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝ コリオリの力をご存知なら，最近また新聞に載った【回転ゆで卵の立ち上がり】の問題 を考えて下さい．寿司屋の湯飲みでも，こたつの天板の上で見事に立ち上がりますよ． それから，一般力学で力をやたらと意味のない方向に分けて考えるのは誤りの原因です．

山旅人 さんのレス (2006/04/22(Sat) 14:10)

ベンさん，初めまして．山旅人と申します．まだご覧になっていらっしゃいますでしょうか． お尋ねへの回答は，yamaさんのそれで尽くされていると思います．が，蛇足をひとつ…

> 数式をいじっていったら，変な項がでてきて，しかもそれで感覚上のことが説明できたなんて，，，なんか不思議ですね．

感覚上のことを説明し納得しようとした努力の末，慣性系・非慣性系・慣性力などの新しい概念にたどり着いた，と私は思っています．

> 僕がターンテーブルの上にいたら力を感じるわけですよね？(回ってることに気付かなければ何かに引っ張られてると思うはず)それはなぜなんでしょうか？

紛れもなく，「僕」 が加速度運動（円運動）を行っているからです．円運動の向心力は，静止摩擦力です．静止摩擦力には上限があるため，回転の角速度が大きくなっていくと向心力がそれを維持できなくなり，「僕」 は，テーブルの上を滑り始めます．

トンガリさん，初めまして． > コリオリの力をご存知なら，最近また新聞に載った【回転ゆで卵の立ち上がり】の問題を考えて下さい． この記述を 「『回転ゆで卵の立ち上がりはコリオリの力が原因だ』 とおっしゃっている」 と受け取ってよろしいでしょうか？

だとすれば，私は，それはどうか？ と思います．例えば以下のサイトにあるように，非常に複雑なメカニズムが働くようです．

• http://home.p07.itscom.net/strmdrf/dynamics08.htm

トンガリ さんのレス (2006/04/25(Tue) 02:55)

回転座標系とは，曲座標系(Ｒ,Θ)ではなく，慣性座標系をωで回転する座標(ｘ,ｙ)でしたか．それなら，

曲座標系(Ｒ,Θ)で，先に述べた Ｒ＝ｖｔ Θ＝-ωｔ

を回転座標系(ｘ,ｙ)に変換すると， ｘ ＝ｖｔcos(-ωｔ) ｙ ＝ｖｔsin(-ωｔ) すなわち，上記の式が質点の軌道です．問題の答えです．

《おまけ》 慣性力・遠心力・向心力・コリオリの力・運動方程式が，ここでは話題になっているので， 上記の式を微分して速度ベクトルを求めると， ｘ'＝＋ｖｔωsin(-ωｔ)＋ｖcos(-ωｔ) ｙ'＝−ｖｔωcos(-ωｔ)＋ｖsin(-ωｔ)

直行する上記の速度ベクトルを合成すると， 第一の項は 大きさ ｖｔω 換言すると Ｒω で反回転方向に向かう． 第二の項は 大きさ ｖ で半径が広がる方向に向かう． ここまでは感覚的に矛盾はないと思う．

上記の速度ベクトルを微分して加速度ベクトルを求めると， ｘ"＝[−ｖｔω^2cos(-ωｔ)＋ｖωsin(-ωｔ)]＋ｖωsin(-ωｔ) ｙ"＝[−ｖｔω^2sin(-ωｔ)−ｖωcos(-ωｔ)]−ｖωcos(-ωｔ)

上記の加速度ベクトルを整理すると， ｘ"＝−ｖｔω^2cos(-ωｔ)＋2ωｖsin(-ωｔ) ｙ"＝−ｖｔω^2sin(-ωｔ)−2ωｖcos(-ωｔ) 回転座標系での運動方程式は，正しくは，上記の加速度ベクトルに質量mを掛けた式です．

直行する上記の加速度ベクトルを合成すると， 第一の項は 大きさ ｖｔω^2 換言すると Ｒω^2 で半径が狭まる方向に向かう．質量mを掛けて【向心力】です． 第二の項は 大きさ 2ωｖで反回転方向（【向心力】と90度を成す）に向かう．質量mを掛けて【コリオリの力の一例】です．

慣性標系(Ｘ,Ｙ)での一例 Ｘ＝ｖｔ，Ｙ＝0 の等速直線運動を 回転座標系(ｘ,ｙ)で見ると， 回転座標系の２種類の慣性力（質量に起因する力）とも呼ぶべき，【向心力】と【コリオリの力の一例】が作用している．

以上力作のつもりです．関数の微分に間違いがないか検算願います．

《蛇足》 【向心力】は摩擦力ではありません．回転座標系で見ると見える慣性力の１っです． 車が急カーブを切ると，回転中心に向かってタイヤに摩擦力が働きます．この力が向心力です． 向心力があるからこそ曲がれるのです．運転者は向心力とは反対方向の遠心力を感じます． これにて，以後修正を止めますと言いましたが，また修正してしまいました．最後の正直にします．

yama さんのレス (2006/04/26(Wed) 00:08)

トンガリさん，詳しい考察，ご苦労様です．

トンガリさんは，【向心力】と向心力を異なる意味に使い分けておられますね． ただ【】をつけているとはいえ，同じ用語を用いるのは誤解を招くおそれがあるのではないかと心配します． それはともかくとしても，回転座標系での慣性力を，【向心力】と【コリオリの力の一例】としている点は疑問です． 【向心力】と【コリオリの力の一部】とすれば辻褄は合うと思いますが，それでも一般的な定式化とは異なっているので，混乱を引き起こすおそれがあります． つまり，回転座標系での慣性力は，一般的には遠心力とコリオリの力に分けて考えますが，あなたの定式化では，遠心力が見かけ上消えてしまっているからです．

具体的に考えてみましょう． あなたが書かれた加速度の式の第一項は確かに中心に向かうので，質量を掛けたものは見かけ上向心力のように見えます．（もちろん本当の向心力ではありませんが） しかし第二項は円周方向に向かうので質量を掛けてもコリオリの力にはなりません．コリオリの力の向きは速度に垂直であって円周方向ではないからです． 第二項に質量を掛けたものは，コリオリの力の円周方向の成分です． つまり【コリオリの力の一部】であって【コリオリの力の一例】ではありません． それでは，コリオリの力の動径方向の成分はどうなっているのかというと，それは第一項に質量を掛けたものの中に含まれています．また，第一項に質量を掛けたものの中にはこの他に遠心力も含まれています．つまり，あなたが言われる【向心力】はコリオリの力の動径方向の分力と遠心力の合力です． したがって慣性力全体は，遠心力とコリオリの力の合力になります．つまり 慣性力＝【向心力】＋コリオリの力の円周方向の分力 ＝遠心力＋コリオリの力の動径方向の分力＋コリオリの力の円周方向の分力 ＝遠心力＋コリオリの力 ということです． このことは，加速度の式が次のように書き換えられることからもわかります． ｘ"＝ｖｔω^2cos(-ωｔ)＋2ωｙ' ｙ"＝ｖｔω^2sin(-ωｔ)−2ωｘ' 第一項は中心から外側に向かい，質量を掛けたものは遠心力です． 第二項は速度（ｘ',ｙ'）に垂直で，質量を掛けたものはコリオリの力です．

トンガリ さんのレス (2006/04/26(Wed) 12:21)

yamaさんへの反論が煩雑になるのを避けるために，下記の Yes，No の設問を試みました．お答え下さい．

＜一般的な回転運動＞ の私の主張 １．慣性座標系で，半径Ｒ 角速度ωで回転している質量ｍに働く力は， ｍＲω^2 の向心力のみである． ２．回転座標系で，半径Ｒ 角速度ωで回転している質量ｍに働く力は， ｍＲω^2 の向心力のみである． ３．上記に遠心力が見当たらないが，それで正しい．ただし，質量ｍに搭乗している人は遠心力を感じる． ４．機械設計者には，向心力は外力で，遠心力は内力である．釣合・運動を考えるとき内力を無視する．

＜慣性座標系で記述された運動方程式を回転座標に座標変換＞ の私の主張 ５．慣性座標系で Ｘ＝ｖｔ，Ｙ=0 の軌跡は 回転座標で ｘ ＝ｖｔcos(-ωｔ)，ｙ ＝ｖｔsin(-ωｔ)である．

６．上記５．の回転座標内での軌跡を実現させる回転座標内での速度は，前記軌跡を微分した ｘ'＝＋ｖｔωsin(-ωｔ)＋ｖcos(-ωｔ) ｙ'＝−ｖｔωcos(-ωｔ)＋ｖsin(-ωｔ) である．

７．上記６．の回転座標内での速度を実現させる回転座標内での加速度は，前記速度を微分した ｘ"＝−ｖｔω^2cos(-ωｔ)＋2ωｖsin(-ωｔ) ｙ"＝−ｖｔω^2sin(-ωｔ)−2ωｖcos(-ωｔ) である．

８．慣性座標系で Ｘ＝ｖｔ ，Ｙ=0 記述された運動方程式を回転座標に座標変換すると ｍｘ"＝−ｍｖｔω^2cos(-ωｔ)＋2ｍωｖsin(-ωｔ) ｍｙ"＝−ｍｖｔω^2sin(-ωｔ)−2ｍωｖcos(-ωｔ) である．

９．上記８．に誤りがなければ，ニュートンを信じる者にとっては，コリオリの又聞きに反しても平気である．

＜追伸＞ コリオリの力は，『 見かけの力が働いているように観測される・・・ 』とかで，私には整理ができてません． 振動ジャイロでは，コリオリの力（重要なことは一例ではｖに垂直な方向に働く）を実測してωを算出している． コリオリの力は実際に在るのです．だから，『 見かけの力・・・』との言い方は止める方向で整理したいのです．

トンガリ さんのレス (2006/04/26(Wed) 12:42)

地球は回転座標系か 私にも常に遠心力が働いているな． 赤道付近では遠心力が最大になるな． 何か私，間違っているみたい・・・特に２．は・・・

ｙama さんのレス (2006/04/26(Wed) 15:37)

設問が反論になっているようには見えませんが，一応回答しておきます．

１．Yes ２．No 回転座標系自体の回転の角速度をω'とすると，ｍＲ(ω'+ω)^2 の向心力がはたらきます． ３．１．については Yes，２．については運動方程式に慣性力の項が必要になります． ４．内力，外力という語が，物理で一般的に用いられている意味とは異なる意味に用いられているようですが，それ以上のことはなんとも言えません． ５．Yes（No.9057で実質的に同じことを書いています．） ６．〜８．Yes（No.9158では，これらの式が間違っているとは言っていません．これらの式が正しいことを認めた上で，式の解釈を問題にしているのです．） ９．意味が理解できないので回答不能です．

＜追伸＞について 「見かけの力」というのは，非慣性系でのみはたらくように見える力ということです．慣性系に移ると見かけの力は消失します．ただし，非慣性系のみの観測で慣性力と本物の力を区別できるかというと，ちょっと微妙な点はあります．慣性力と重力が局所的には区別できないという等価原理に基づいて一般相対性理論がつくられたことはよく知られています． しかし，ニュートン力学に関する限り，見かけの力である慣性力と本物の力ははっきり区別されます．ほとんどの力学の本はそれを前提として慣性力を論じていますし，私もそれを前提に書いています． 『 見かけの力・・・』との言い方は止める方向で整理したいとのことですが，ぜひ整理して発表してください．楽しみにしています．

ところで，私が No.9158 で書いたことについての反論がないようですが・・・ No.9158 では，あなたが書いた加速度の式の第二項に質量を掛けたものはコリオリの力ではないと主張しています．詳しく言うと，コリオリの力の円周方向の成分だけを表していて，コリオリの力全体を表してはいないということです．これについての反論を期待します．

トンガリ さんのレス (2006/04/26(Wed) 16:42)

おっしゃる通り反論になっていません．実はコリオリの力についてよく知らないので反論できないのです． それでも，間繋なぎの設問にお答え頂き，理解が少しは進んだ気がします 今でも，私はyamaさんの御指摘を十分理解してません．これから熟読させて頂きます．

例題の場合，コリオリの力の半径方向の成分は在るのでしょうか．在るとしたら，どんな式でしょうか． 仮に無ければ，【コリオリの力の一例】＝ コリオリの力の円周方向の成分だけ となって，争点が消えます．

反論すべきところを，どうしても質問になってしまって，すみません． コリオリの力について整理するのは，全てを明ら様にしてからですから，今はとてもとても出来ません． 仕事が入っているので，小休止します．工作機械を動かしながら考えます．

ｙama さんのレス (2006/04/26(Wed) 17:30)

>例題の場合，コリオリの力の半径方向の成分は在るのでしょうか．在るとしたら，どんな式でしょうか．

あります．その式は ｘ成分＝−2ｍｖｔω^2cos(-ωｔ) ｙ成分＝−2ｍｖｔω^2sin(-ωｔ) です． これは，遠心力の2倍の大きさで，遠心力と逆に中心に向かってはたらきます． なお，遠心力は ｘ成分＝ｍｖｔω^2cos(-ωｔ) ｙ成分＝ｍｖｔω^2sin(-ωｔ) なので，これらの合力は ｘ成分＝−ｍｖｔω^2cos(-ωｔ) ｙ成分＝−ｍｖｔω^2sin(-ωｔ) となります．これがあなたが言われる【向心力】です．