ゆう さんの書込 (2006/09/02(Sat) 11:33)

はじめまして，工学部の一年生です． 摩擦のない水平面上で直線運動をして，速度の２乗に比例した空気抵抗を受ける場合 速度の式と位置の式はどのようになるのでしょうか？

こちらの「抵抗力のある落下運動」はとても参考になり，鉛直方向に落下し空気抵抗を受ける場合についてはなんとか分かりました．

まず運動方程式が次の式で与えられています．

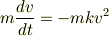
この運動方程式を解くとこのようになるのかなと思ったのですが

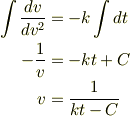
しかし，教科書の答えでは

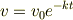
となるようです．

どこか解き方が間違えているでしょうか？

mNeji さんのレス (2006/09/02(Sat) 12:15)

はじめまして．

変数分離した左辺が間違えているとおもいます．もう一度，見直しましょう．指数関数はでないと思いますが．

いま，時間がないので...．

mNeji さんのレス (2006/09/02(Sat) 12:28)

間違えました，御免なさい．

左辺の分母が違うので，間違われたとかんちがいしました．

お示しされた解で良いとおもいます．t=0で 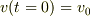などと置くと見やすい式になりますね．

ゆう さんのレス (2006/09/02(Sat) 22:56)

こんばんは． mNejiさん，お返事ありがとうございます．

そうですか，これで良かったのですね． もう一度確認してみます．

それと，一言みなさんにお礼が言いたくて 昨年質問させていただきまして，その時受験生だったのですが，なんとか無事大学に合格することが出来ました． このサイトにはとてもお世話になっています． これからも頑張って下さい．

• http://hooktail.maxwell.jp/bbslog/7011.html

Joh さんのレス (2006/09/02(Sat) 23:12)

ゆうさん，

合格おめでとうございました！！ このサイトがお役に立ったということで，そう言って頂けると 本当に嬉しいです．

また，気軽にお越し下さい．（そして，宜しければ メンバーになりませんか？）

今回のように，答えがおかしいかなと思った場合には，検算の意味で 逆に運動方程式を立ててみてもいいかも知れませんね．時間で 微分して，mを掛けて．．．っていう感じで．

mNeji さんのレス (2006/09/03(Sun) 00:19)

朝は慌てて回答して済みませんでした．

1. 意見

物理の回答は，数学の回答のように任意定数Cのままにするは間違えの基と思います．適切な初期条件をつけて変形したほうがわかりやすく，チェックもイメージし易いと思います.

初期条件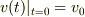， とすると，

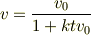
運動方程式から次元解析をしますと ・[kdt]=[dv/(v^2)]=[1/v] --> [ktv]=[kdt][v]=1 故にOK.

微分方程式の解ｖが出来たら，元の微分方程式を満たすかにより検算しましょう．

2. 質問A

近くのスレッドにも論議されていますが，抵抗の係数に「m」が入っているのがとても奇妙に感じます．宜しければ，出典をお教えくださいますか？

3. 質問B：LaTeX友の会・収集係として

過去の質問を拝見しましたが，高校生のときにLaTeXをお使いのようですが，自習で判ったのでしょうか，それとも近くの人から教えていただいたのでしょうか？

ゆう さんのレス (2006/09/03(Sun) 11:12)

こんにちは． みなさん，ご回答ありがとうございます．

> 任意定数Cのままに・・・

そうですね，今度から初期条件をつけるようにいたします．

> 抵抗の係数に「m」が・・・出典を・・・

質量によって抵抗力が変化するというのは，ちょっと奇妙な感じがしますよね． 出典は教科書です．なのですが，担当の先生が書いた本なので学校が分かってしまいます．．． メールなどであれば可能です．

> LaTeX友の会・収集係として

高校生でLaTeX使ってたらすごいんですけどね． 僕は今３１歳なのです． コンピュータは趣味や仕事で使っているので得意なのですが，数学や物理は苦手で・・・今年初めて微分，積分を勉強しました．

> Johさん

お誘いありがとうございます． しかし，残念ながら僕には物理などを解説できるだけの知識はなさそうです．

それでは，またよろしくお願いします．

mNeji さんのレス (2006/09/03(Sun) 12:56)

ゆうさん：

>メールなどであれば可能です．

状況がわかりました．教科書にもミスはあると考える事にします．回答いただき感謝します．

>僕は今３１歳なのです． >コンピュータは趣味や仕事で使っているので得意なのですが，数学や物理は苦手で・・・今年初めて微分，積分を勉強しました．

私も，60-α歳にして，物理を再開した者です．このサイトにあるJohさんの記事を拝見して，数学と物理が密接な関係にあるのを今頃理解して，勉強させていただいてます．

この数学掲示版は，高校生さんや大学生さんのQ&Aが主目的と思いますが，我々，一般市民のQ&Aの場でもいいわけですよね．ドンドン，ご質問なさったら善いですね．

>しかし，残念ながら僕には物理などを解説できるだけの知識はなさそうです．

「質問が出てくる」事が大切で，それを自分で解決できるのも凄いですが，「判らない点」を公開して，色々な人達と論議しながら「正しい答えを得る」のもまた別の醍醐味かも知れませんね．