等加速度運動の方程式について
等加速度運動の方程式について
ユウ さんの書込 (2005/10/16(Sun) 20:41)
初めまして,30にして大学受験をしようと思っているユウといいます. すっかり物理の事は忘れており,最近はじめたばかりで,以下の問題でつまづいており 教えていただけないでしょうか?
−問題 なめらかな定滑車に糸を介して質量Mの物体Aと質量mの物体Bが吊り下げられている. 最初Bは水平な底面に,Aは底面から高さhの位置にあり,そこからAは床に向かって落ち始めた. 重力加速度の大きさをgとしたとき,Aが床に落下した瞬間のBの速さはいくらか?
という問題で まず,物体Aの運動方程式を考えました.
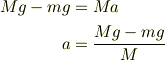
加速度aを求めて,等加速度運動の方程式から,高さh落下した時の速度を求めました.
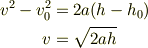
先ほど求めたaを代入しました.
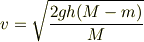
となるのかなと思ったのですが,解答では,力学的エネルギー保存則を用いて以下の式になっていましたが 何故このような解答になるのでしょうか?
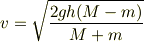
Re: 等加速度運動の方程式について
tomo さんのレス (2005/10/16(Sun) 23:31)
ユウさん,初めまして. tomoです.
運動方程式が違っています.それぞれの物体にかかる力は,絵に描かれたでしょうか?
物体Aには,重力と糸の張力( 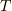 )がかかっていますよね.
物体Aの運動方程式に
)がかかっていますよね.
物体Aの運動方程式に 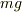 という項が出てくるのはおかしいはずです.
という項が出てくるのはおかしいはずです.
加速度を  とすると,物体Aの運動方程式は,
とすると,物体Aの運動方程式は,
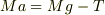 ですね.物体Bの運動方程式も立てて,連立してみてください.正しい加速度が求まります.
ですね.物体Bの運動方程式も立てて,連立してみてください.正しい加速度が求まります.
加速度が求まったら,等加速度運動の式を用いても,エネルギー保存則を用いても, 正しい答えが得られるはずです.がんばってください :)
#物体Bについての"力のつりあいの式"から, 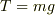 として,
#物体Aの運動方程式にこの"式"を代入されたのかもしれませんが,
#この問題では物体Bも動いていますので,力はつりあっていません.
として,
#物体Aの運動方程式にこの"式"を代入されたのかもしれませんが,
#この問題では物体Bも動いていますので,力はつりあっていません.
Re: 等加速度運動の方程式について
ユウ さんのレス (2005/10/16(Sun) 23:56)
初めまして,tomoさん.
回答ありがとうございます. 物体Aの方は絵を書いていたのですが,Bの方は楽をしようと書いていませんでした... あと,力はつりあっていないんですね. もう一度書いたところ
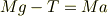
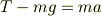
これを物体Aの方の式に代入すると
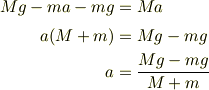
となり
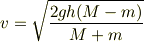
となりました. tomoさんありがとうございました.
Re: 等加速度運動の方程式について
tomo さんのレス (2005/10/17(Mon) 00:25)
ユウさん,こんばんは.
良かったです :)
蛇足ですが,
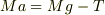
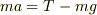
から  を求める際,両辺を足してしまうと,(少〜し)計算が速いです.
この問題だと素直に代入法でやってもあまり差はないですけどね(笑).
運動方程式が3つや4つになると,「両辺を足す」というのが有効な場合があります.
を求める際,両辺を足してしまうと,(少〜し)計算が速いです.
この問題だと素直に代入法でやってもあまり差はないですけどね(笑).
運動方程式が3つや4つになると,「両辺を足す」というのが有効な場合があります.
また,得られた結果
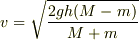
を見て,「  と
と  の差
の差 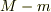 が大きいと
が大きいと  も大きい」とか,
「
も大きい」とか,
「  と
と  の差
の差 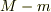 が小さいと
が小さいと  も小さい」など,
特徴的なケースについて,(自分の感覚と合っているかどうか)考えてみるのも良いです.
たとえば,答えが
も小さい」など,
特徴的なケースについて,(自分の感覚と合っているかどうか)考えてみるのも良いです.
たとえば,答えが 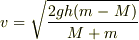 と求まった場合には,
なんかおかしいぞ,どこかで間違えたかなと思えます.
と求まった場合には,
なんかおかしいぞ,どこかで間違えたかなと思えます.