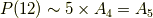この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
正多面体群2
正四面体群,正六面体群,正八面体群,正十二面体群,正二十面体群の位数は,それぞれ 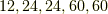 だということでした. 正多面体群1 では,元の数を頑張って全部数え上げましたが,もう少しスマートに位数を求める方法を考えます.
だということでした. 正多面体群1 では,元の数を頑張って全部数え上げましたが,もう少しスマートに位数を求める方法を考えます.
正四面体群
正四面体を自分自身に重ねる回転には,二種類の軸がありました.頂点とそれに向かい合う面の中心を通る軸と,相対する二辺の中点を結んだ軸です.これらの変換に対して,頂点(  と名づける)がどのように置換されるかを見ましょう.
と名づける)がどのように置換されるかを見ましょう.
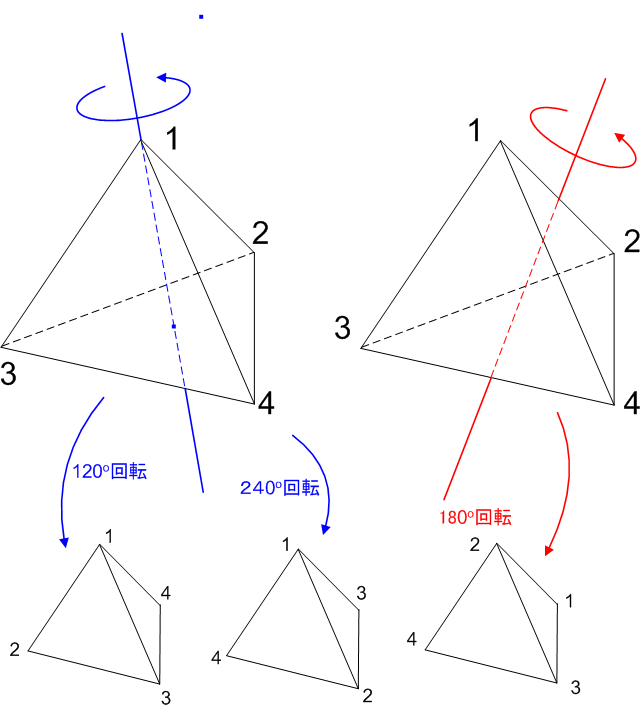
まず,図中,左側の変換では,頂点 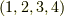 が
が 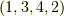 か
か 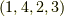 に移されます.これらの変換は,次のように表わせます.
に移されます.これらの変換は,次のように表わせます.
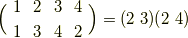
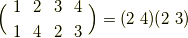
頂点 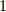 を通る軸の周りに回す回転では,頂点
を通る軸の周りに回す回転では,頂点 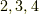 が巡回置換を受けます.可能な置換は,この2つと単位置換しかないことがわかりました.すべて偶置換で表わされていることに着目して下さい.
が巡回置換を受けます.可能な置換は,この2つと単位置換しかないことがわかりました.すべて偶置換で表わされていることに着目して下さい.
一方,図の右側の変換では,頂点 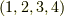 が
が 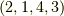 に移されています.この変換は次のように表わせます.これも偶置換です.
に移されています.この変換は次のように表わせます.これも偶置換です.
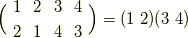
すなわち,正四面体群 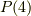 の元による,正四面体の頂点の移動には,偶置換しかないということです.
の元による,正四面体の頂点の移動には,偶置換しかないということです. 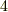 次の対称群
次の対称群 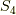 の元で,偶置換になるのは,上の二つのタイプと単位置換で全部ですから,正四面体群
の元で,偶置換になるのは,上の二つのタイプと単位置換で全部ですから,正四面体群 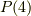 は
は 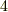 次の偶置換で生成された群,すなわち
次の偶置換で生成された群,すなわち 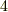 次の交代群
次の交代群 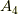 と同型だと言えるわけです.(単位置換も偶置換であることは 対称群 を参照してください.)
と同型だと言えるわけです.(単位置換も偶置換であることは 対称群 を参照してください.)
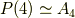
これにより,正四面体群 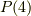 の位数は,交代群の位数の公式を使って,ただちに次のように求まります.
の位数は,交代群の位数の公式を使って,ただちに次のように求まります.
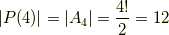
回転の種類を全部数え上げるのと,そんなに労力は変わらなかったかも知れませんが,交代群と関連づけられたのが,ちょっと新鮮ではありませんでしたか?
正六面体群と正八面体
正六面体群の位数は,対角線の置換だと考え,次のように求められることを既に見ました.( 正六面体群 を参照.)
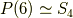
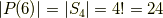
ところで,正六面体の面の中心を結ぶと,内接する正八面体が描けます.逆に,正八面体の各面の中心を結ぶと,やはり内接する正六面体が描けます.
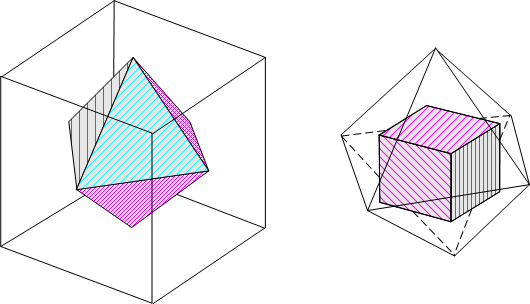
このような双対関係により,正六面体を不動に保つ変換と,正八面体を不動に保つ変換は完全に対応していることが言えます.(どちらかを変換するとき,内接するもう一方の図形を心の目で見てください.この二つの図形は,実は一蓮托生だったのです.)
これにより,ただちに次の関係が言えます.
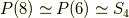
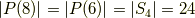
| [*] | 例えば,正六面体の各面の中心の点にだけ印をつけ,正六面体群の元である回転操作を加えたときの軌跡は正八面体の動きになり,同様に,正八面体群の元である回転操作を正八面体に加えたとき,各面の中心の軌跡は正六面体の動きになるということです.面白いですね! |
正十二面体と正二十面体
実は,正十二面体と正二十面体も双対関係にあり,どちらかの面の中心を結ぶと,もう片方の図形が内接する形で得られるのです.この関係に気づけば,ただちに次の式が言えます.
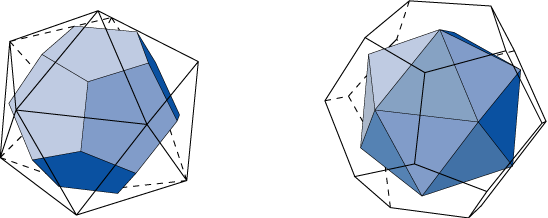
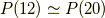
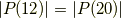
どおりで,正十二面体群と正二十面体群の位数は同じだったわけです.
また,正十二面体や正二十面体でも,(正四面体で先に示したように)頂点の動きに着目すれば, 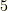 次の交代群に同型だということが分かります.証明は次節に書きますので,興味のある人だけ見てください.ここには結果だけを書いておきます.
次の交代群に同型だということが分かります.証明は次節に書きますので,興味のある人だけ見てください.ここには結果だけを書いておきます.
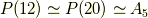
| [†] | 正六面体と正八面体,正十二面体と正二十面体はそれぞれ双対関係にあると言われます.双対な多面体は,面と頂点の関係が互いに逆になっている多面体ですので,上で行ったように各面の中心を結ぶと内接する双対多面体が現われますし,各頂点に面を外接させても双対多面体が現われます. 正多面体群1 の表で一つの頂点に集まる辺の数 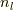 と,一つの面が持つ頂点の数が と,一つの面が持つ頂点の数が 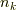 双対多面体では互いに逆になっていることを確認してみてください.正四面体は各面の中心を結ぶと同じく正四面体が出てきますから,自己双対だと言われます.双対な多面体群を同じものだと見なし,本質的に三次元の多面体群には 双対多面体では互いに逆になっていることを確認してみてください.正四面体は各面の中心を結ぶと同じく正四面体が出てきますから,自己双対だと言われます.双対な多面体群を同じものだと見なし,本質的に三次元の多面体群には 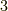 種類しかないという見方もできます. 種類しかないという見方もできます. |
補
正十二面体が 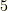 次の交代群に対応することは,当初面倒なので結果しか示さなかったのですが,要望があったのでここに補足します.
次の交代群に対応することは,当初面倒なので結果しか示さなかったのですが,要望があったのでここに補足します.
正十二面体の面は正五角形をしていますので,星型に五本の対角線が引けます.
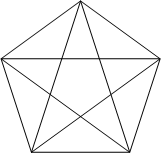
この対角線の一つを一辺とする正六面体を正十二面体の中に内接させることができます.次図のように,これには五種類あります.

正十二面体はちょうど,正六面体の一つの面に切妻屋根を乗せたような形になっているわけですね.
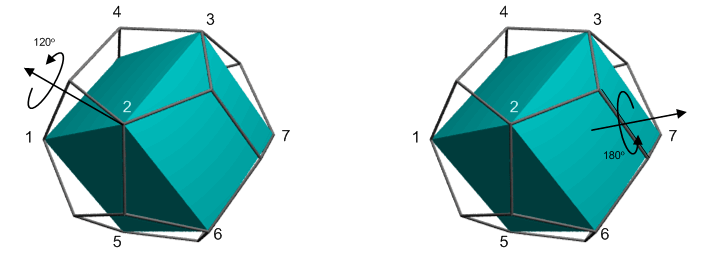
さて,上の図のうちの一つだけに注目しましょう.正十二面体群の元のうち,内接する正六面体を正六面体自身に移す変換は,もちろん正十二面体も正十二面体自身に移します.そこで,正十二面体群の元で,内接する正六面体をも保つものをまず考えます.左から四番目のものが見やすいと思います.
まず正六面体の頂点を通る対角線を軸に, 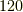 度もしくは
度もしくは 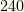 回す変換があります.対角線は
回す変換があります.対角線は 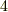 本ありますので,この種類の変換が計
本ありますので,この種類の変換が計 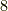 個あります.次に,正六面体の面の中心を通る軸の回りに
個あります.次に,正六面体の面の中心を通る軸の回りに 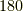 度回す変換があります(この軸は,切妻屋根の稜線の中心を通ります).これが計
度回す変換があります(この軸は,切妻屋根の稜線の中心を通ります).これが計 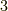 本あります.
本あります. 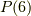 と違うのは,正六面体の各辺の中点を結んだ線を中心に回す変換が無いことです.このような回転は正十二面体の対称性を崩してしまうことがわかるでしょう.
と違うのは,正六面体の各辺の中点を結んだ線を中心に回す変換が無いことです.このような回転は正十二面体の対称性を崩してしまうことがわかるでしょう.
結局,上記の二種類に恒等置換を加えて,正十二面体群のうち,正十二面体も内接する立方体も両方不変に保つものには 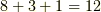 種類あることが分かりました.
種類あることが分かりました. 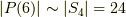 のちょうど半分ですから,位数からだけでもこれが交代群であることが証明できそうですが,念のため,頂点に番号を振って,ここで求めた変換が偶置換であることを示しましょう.
のちょうど半分ですから,位数からだけでもこれが交代群であることが証明できそうですが,念のため,頂点に番号を振って,ここで求めた変換が偶置換であることを示しましょう.
まず,正六面体の対角線回りに 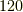 度回す回転を考えると(上左図),頂点は
度回す回転を考えると(上左図),頂点は 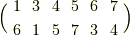 と移されます(図を見て想像して下さい.頂点
と移されます(図を見て想像して下さい.頂点 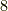 は図では隠れてしまっています).
は図では隠れてしまっています). 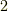 と
と 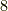 が不動です.この置換は次のように互換の積に分解できます.
が不動です.この置換は次のように互換の積に分解できます.
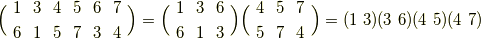
この変換は偶置換であることが分かりました. 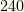 度回す変換は,
度回す変換は, 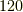 度回す変換の二乗ですから,やはり偶置換です.次に,上図右図の変換を考えましょう.頂点は
度回す変換の二乗ですから,やはり偶置換です.次に,上図右図の変換を考えましょう.頂点は 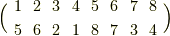 のように変換されます.この置換は次のように互換の積に分解されます.
のように変換されます.この置換は次のように互換の積に分解されます.
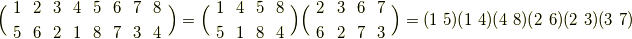
こちらもやはり偶置換であることが分かりました. 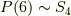 は位数が
は位数が 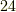 で,そのちょうど半分は偶置換のはずですが,いま求めた変換群は
で,そのちょうど半分は偶置換のはずですが,いま求めた変換群は 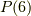 の部分群であり,位数が
の部分群であり,位数が 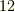 で全て偶置換ですから,これは四次の交代群
で全て偶置換ですから,これは四次の交代群 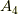 に他なりません.
に他なりません.
正十二面体に正六面体を内接させるさせ方には 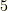 種類ありましたから,次式が成り立ちます.
種類ありましたから,次式が成り立ちます.