この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
オイラー・ラグランジュ方程式の座標非依存性
オイラー・ラグランジュ方程式

は,デカルト座標系で表された場合でも,
極座標で表された時でも,等しく成り立つのでした.
どんな座標系 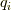 から座標系
から座標系 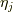 への同次変換
への同次変換
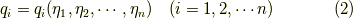
で考えても,オイラー・ラグランジュ方程式が成立することを証明します. 簡単の為,ラグランジアンは時間に依存しないものとします. ある程度分かっている人向けだと思います.
ちょっと復習
そもそもオイラー・ラグランジュ方程式は,どうやって導出されたのでしょうか. 軽く振り返ってみましょう.
自然界では作用 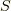 (=ラグランジアン
(=ラグランジアン  の時間積分)と呼ばれる量が停留値を取るように運動がおこります.
これをハミルトンの原理とか,最小作用の原理といいます.
の時間積分)と呼ばれる量が停留値を取るように運動がおこります.
これをハミルトンの原理とか,最小作用の原理といいます.
数式で表すと, 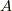 点
点 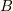 点の間では
点の間では
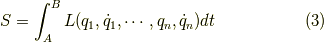
として,その変分を 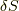 とし,境界項を省略すると,
とし,境界項を省略すると,

このゼロが恒等的に成立するとすると,オイラー・ラグランジュ方程式,
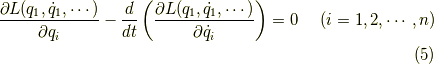
が導かれます.
さぁ,座標変換だ
さて,そろそろ本題に入りましょう.座標変換,
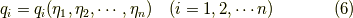
が与えられているとします.
この時には,
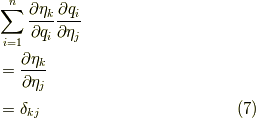
が成立することを確認しておきます.このδはクロネッカーのデルタ記号です.すると,ラグランジアンの一部について,

が成立します.同様に,後半部分も,
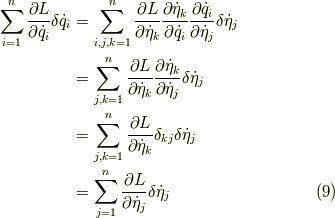
となります.よって,
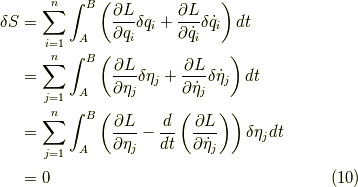
となり,無事,別の座標系 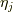 でも恒等的にゼロに等しいので,
オイラー・ラグランジュ方程式の別の座標系での表現,
でも恒等的にゼロに等しいので,
オイラー・ラグランジュ方程式の別の座標系での表現,
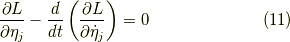
が導けました.今日はここまで,お疲れ様でした.