この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
rotの座標変換
ベクトル解析で出てくるrot(ローテーション,回転)は, 他のデカルト座標系では果たして本当にベクトルとして振舞うのかを 調べてみました.
前の記事は, divの座標変換不変性 です. 次の記事は, gradの座標変換 です.
rotについて基本的なこと
ベクトル 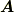 に対して,
に対して, 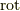 は以下のように
表わされます.デカルト座標系
は以下のように
表わされます.デカルト座標系 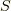 の基底ベクトルを
の基底ベクトルを 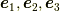 とすると [*] ,
とすると [*] ,
| [*] | : この記事では添え字について, 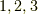 は,それぞれ は,それぞれ 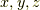 を表すものとします. を表すものとします. |

この式は,エディントンのイプシロンと呼ばれる次の記号を使うと簡単に書けます.
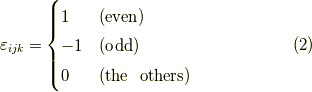
ただし,添え字が偶置換の時を  ,奇置換の時を
,奇置換の時を 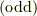 それ以外の3つの添え字の中に同じ数が入る時を
それ以外の3つの添え字の中に同じ数が入る時を 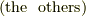 で表わしました.
で表わしました.
大抵,この記号はアインシュタインの縮約という「同じ添え字について,和を取ってΣ記号を省略する」ルール [†] と一緒に用いられます.
| [†] | : たとえば, 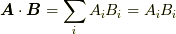 のように三次元ベクトルの内積を表します. のように三次元ベクトルの内積を表します. |
更に,例えば  に関する偏微分を,
に関する偏微分を,  などと書くことにします.
すると,式
などと書くことにします.
すると,式 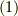 は,
は,

となります.簡潔ですね.
これから,座標の変換を議論します.そこで, divの座標変換不変性 で用いたのと同じ変換行列 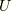 を用います.
を用います.
つまり,座標系 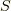 のベクトル
のベクトル 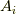 と座標系
と座標系 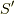 のベクトル
のベクトル 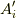 について,
実直交行列
について,
実直交行列 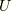 が存在して,次のように表わされます.
が存在して,次のように表わされます.
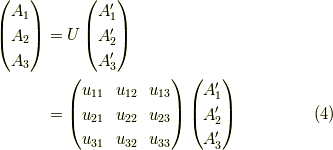
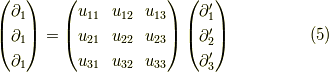
ここで,例えば式 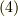 を書き直すと,
を書き直すと,
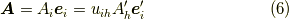
成分を抜き出すと,
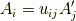
となります. これが,ベクトルの(偏微分も一緒)変換則です. すると,今示したい変換は,

となります.これは,位置ベクトルの「成分」の変換と同様に振舞います [‡] .
| [‡] | 「成分」とカギ括弧をつけたのは,基底ベクトルとは異なる変換をされるからです. 詳しくは, ベクトルの基底の変換 をご覧ください. |
本題
それでは準備が整いましたので,式 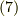 の左辺を計算してみましょう.
の左辺を計算してみましょう.
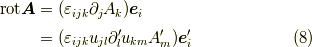
これから先は,成分を抜き出して考えていきます.
例えば,第一成分(  方向の成分)を書き出すと,
方向の成分)を書き出すと,
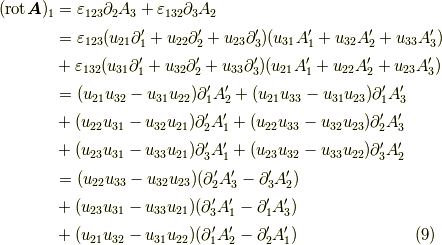
同様に第二,第三成分も書くと,
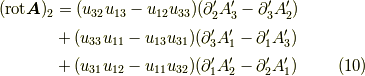
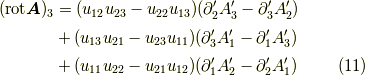
となります.
ここで,行列 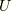 の余因子行列
の余因子行列 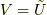 を考えます.これは,逆行列
を考えます.これは,逆行列 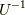 の
の 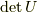 倍であり,
以下のような形をしています.(
倍であり,
以下のような形をしています.( 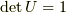 です.)
です.)
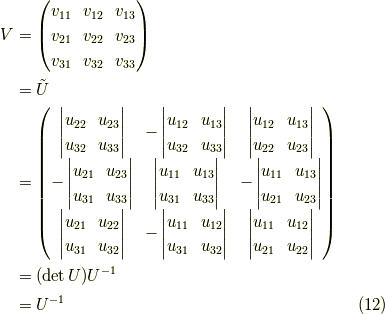

今,行列 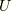 は実直交行列なので,
は実直交行列なので, 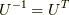 (
(  は転置を表す.)となっています.
よって,
は転置を表す.)となっています.
よって,
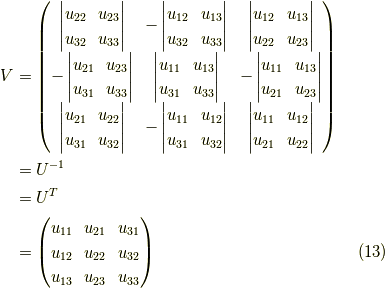
となります.
式 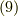 に式
に式 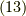 を代入すると,見事に,
を代入すると,見事に,
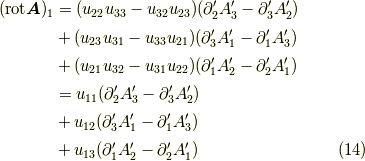
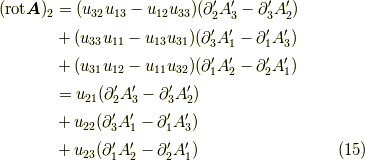
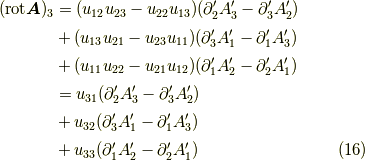
が成り立ちます.
よって無事,式 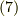 ,
,

が示せました.
それでは,今日はこの辺で.
続きは こちら .