この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
任意の固有値と固有ベクトルを持つ行列の求め方
固有値 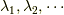 とそれに対応する
互いに線形独立な固有ベクトル
とそれに対応する
互いに線形独立な固有ベクトル 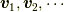 を持つ
行列
を持つ
行列 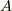 の作り方を考えます.一見,難しそうですが,
結果は簡単です.
の作り方を考えます.一見,難しそうですが,
結果は簡単です.
それでは,さっそく求めてみます.
求めるn次正方行列 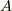 に対し,固有値
に対し,固有値 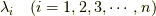 を持つ
列ベクトル
を持つ
列ベクトル 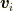 とすると,
とすると,

が成立します. すると,n次の正方行列

同じく行列
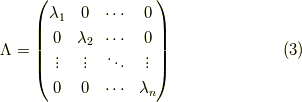
として,まとめて表すことができて,

ここで 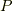 は,線形独立な列ベクトルからなるので,
逆行列が存在して,
は,線形独立な列ベクトルからなるので,
逆行列が存在して,

と求まりました.これは少し変形してやると,
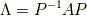
なので,対角化の作業を逆にしたものであることが分かります. なかなか興味深いです.
それでは,今日はこの辺で.