この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
フーリエ変換はある種のπ/2回転と見れること
最近,フーリエ変換は回転の様なものだと別の二人の方からお聞きしました. 最初,何を言っているか分からなかったのですが, 流石に何度も聞くと「ちょっと考えてみるか」と言う気分になり考えてみて, やっといい具体例が見つかったので記事にします. あんまり説明は要らないと思うので,もっぱら数式を書いていきます.
フーリエ変換を何度も行う
フーリエ変換を次の様に定めます.
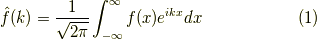
ここで

と置くと,
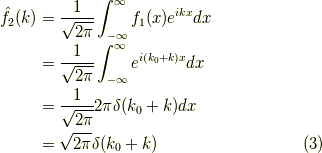
これで一回目です.次に変数の 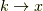 の置き換えをしてフーリエ変換すれば,
の置き換えをしてフーリエ変換すれば,
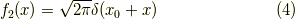
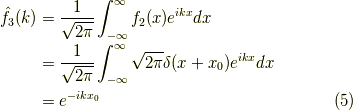
となります.次に行きましょう!

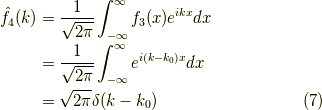
ここで,敢えて 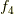 ではなく
ではなく 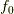 とします.理由は後で分かります.すると,
とします.理由は後で分かります.すると,
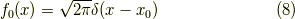
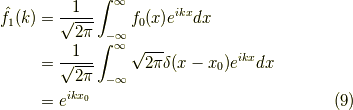
つまり,

となり,これは式 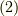 ですね!
ですね!
つまり,フーリエ変換は線形ですから,
任意の関数 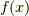 は積分核
は積分核 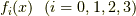 のどれか一つの
のどれか一つの 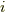 に属する関数だけの重ね合わせで書けます.
それぞれの積分核が4回で元に戻るので,これは
に属する関数だけの重ね合わせで書けます.
それぞれの積分核が4回で元に戻るので,これは  と
と 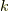 の入れ替えを除いて,
の入れ替えを除いて,
![\mathcal{F}^4[f(x)] = \mathcal{F}[\mathcal{F}[\mathcal{F}[\mathcal{F}[f(x)]]]] = f(x) \tag{11}](http://hooktail.maxwell.jp/kagi/5d772629b6356ed456dfe9789f0ffbfb.png)
であることを示しています.さらに言えば,二回のフーリエ変換では
![\mathcal{F}^2[f(x)] = \mathcal{F}[\mathcal{F}[f(x)]] = f(-x) \tag{12}](http://hooktail.maxwell.jp/kagi/5e643f4dfe936a7dafa5e2051ede5a9f.png)
が言えます.しかし,だからといって,
![\mathcal{F}[f(x)] \neq f(ix) \tag{13}](http://hooktail.maxwell.jp/kagi/620789581cd961e7986164043cbe9cce.png)
であることにはご注意ください.この事により,確かにフーリエ変換というものは,虚数単位 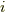 の様に四回行うと元に戻るので
の様に四回行うと元に戻るので 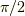 回転と似ていますね.
回転と似ていますね.
この話には続きがあって,整数回のフーリエ変換を実数回に拡張した話が 赤げふさんのページ に書いてあるので,興味がある方はご覧になられるといいと思います.今日はここまで,お疲れさまでした!