この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
偏微分方程式を解く
量子力学の主役「シュレディンガー方程式」をはじめ,物理では偏微分方程式を使うことがよくあります. この方程式の解き方をなんとかマスターしようということで,少々大変ですが偏微分方程式を解いてみましょう.
1次元波動方程式の例題
いまから解いてみるのは1次元波動方程式
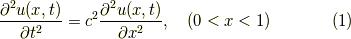
です.ここで  は波の速さで,正の定数です.
偏微分方程式を完全に解くには境界条件と初期条件が必要ですから,
は波の速さで,正の定数です.
偏微分方程式を完全に解くには境界条件と初期条件が必要ですから,
境界条件 : 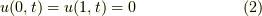
初期条件 : 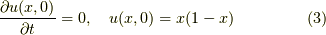
を課しておきます.波動方程式という名前は凄そうですが,ただ単に波の運動をあらわす式です.
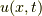 が波の関数で,これに境界条件と初期条件を付け加えることで
この波がどんな運動をしているのかを知ることができます.
つまり「解く」というのは 式(1) を
が波の関数で,これに境界条件と初期条件を付け加えることで
この波がどんな運動をしているのかを知ることができます.
つまり「解く」というのは 式(1) を 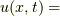 の形にするという事です.
の形にするという事です.
ところで,波の運動というのがイマイチわかりません. 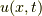 を波の高さだと考えるとどうでしょうか.
を波の高さだと考えるとどうでしょうか.
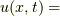 という形になっていたら,
という形になっていたら,  と
と  を代入することで
を代入することで 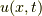 の値が決まります.
つまり波がいつ(時間
の値が決まります.
つまり波がいつ(時間  ),どこで(位置
),どこで(位置  )どんな高さなのか(波の高さ
)どんな高さなのか(波の高さ  )が分かるようになりますね.
)が分かるようになりますね.
そうすると,たとえば初期状態から 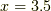 メートルの場所で 2.4 秒後の波の高さは -1.3 メートルで,
メートルの場所で 2.4 秒後の波の高さは -1.3 メートルで,
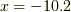 メートルの場所で
メートルの場所で 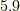 秒後の波の高さは
秒後の波の高さは 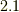 メートルだよ,とすぐに計算できます.
これらを全部ひっくるめてあるのが波動方程式で,様々な条件(境界条件,初期条件)
での波を導き出す操作が波動方程式を解く,ということになります.
メートルだよ,とすぐに計算できます.
これらを全部ひっくるめてあるのが波動方程式で,様々な条件(境界条件,初期条件)
での波を導き出す操作が波動方程式を解く,ということになります.
まずは変数分離
 と
と  の2つの変数がある偏微分方程式では難しいので,変数を分離して2つの常微分方程式に分けます.
変数を分離するには,
の2つの変数がある偏微分方程式では難しいので,変数を分離して2つの常微分方程式に分けます.
変数を分離するには, 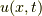 の解として
の解として
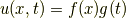
を代入するのが定石です.実際に波動方程式に代入すると
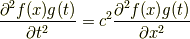
となります.左辺は  で偏微分してあるので
で偏微分してあるので  の関数は関係ないですね.
だから
の関数は関係ないですね.
だから  の関数である
の関数である 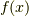 を偏微分から出しておきます.
を偏微分から出しておきます.
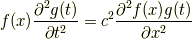
同様に右辺は 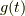 を偏微分から出しておきます.
を偏微分から出しておきます.
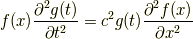
左辺は  の関数,右辺は
の関数,右辺は  の関数にまとめたいので,
両辺を
の関数にまとめたいので,
両辺を 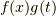 で割ります.ついでに
で割ります.ついでに 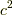 も移動すると
も移動すると
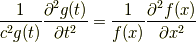
となります.さて,この式は何を意味しるんでしょうか? 左側は  の関数,右側は
の関数,右側は  の関数です.
両辺がイコールで結ばれているので「
の関数です.
両辺がイコールで結ばれているので「  だけ変化しても,
だけ変化しても,  だけ変化しても両辺は等しくなる」ということをいっています.
だけ変化しても両辺は等しくなる」ということをいっています.
そんなことが起きるのは両辺が定数のときだけです.
定数なら  だけ変わろうが
だけ変わろうが  だけ変わろうが,
だけ変わろうが,  と
と  が同時に変わろうが関係ありません.
そこで,この両辺を
が同時に変わろうが関係ありません.
そこで,この両辺を
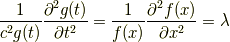
というふうに定数  と等しいとします(この定数は変数分離定数と呼ばれます).
するとこの式は,つぎのように簡単に2つに分けることができます.
と等しいとします(この定数は変数分離定数と呼ばれます).
するとこの式は,つぎのように簡単に2つに分けることができます.
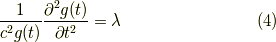
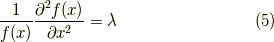
この2式はそれぞれ変数が一つなのでもはや偏微分方程式でなく,常微分方程式です.
変数分離定数  を導入することによって,
偏微分方程式を二つの常微分方程式に分けることができたのですね.
を導入することによって,
偏微分方程式を二つの常微分方程式に分けることができたのですね.
分離した常微分方程式を解く
二つの常微分方程式に分けることができたので,今度はそれらを一つずつ解いて行きます.
まずは  に関する微分方程 式(5) を解きましょう. 式(5) は少し変形すると
に関する微分方程 式(5) を解きましょう. 式(5) は少し変形すると
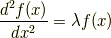
です.これに解として 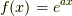 を代入すると
を代入すると

になります.そして

より 式(6) は
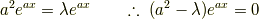
となります.ここで 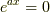 とすればこの方程式を満たしますが,この場合は考えません.
だってそうすると
とすればこの方程式を満たしますが,この場合は考えません.
だってそうすると 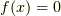 となって意味がないでしょう.ということは,
となって意味がないでしょう.ということは,

となりますね.この式から  を決定します.
を決定します.
ここで注意が必要です.  はまだどんな値かさっぱり分からないので,
はまだどんな値かさっぱり分からないので,
 が正,ゼロ,負の三つの場合で場合分けして考えないといけません.
が正,ゼロ,負の三つの場合で場合分けして考えないといけません.
λ が正の場合
式(7) より
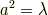
ですね.いまは  が正の場合を考えているので,そのままルートを付けてかまいません.すると
が正の場合を考えているので,そのままルートを付けてかまいません.すると
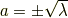
です. 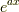 を解として代入したのですから,解は
を解として代入したのですから,解は
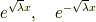
の二つです.一般解はこれらの線形結合で書けて
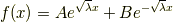
となります(  は任意定数).ここで境界条件
は任意定数).ここで境界条件 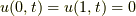 を使います.
いまは
を使います.
いまは 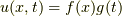 としてるから
としてるから 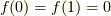 です.したがって
です.したがって
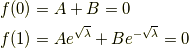
です.これから定数  を求めてみます.
を求めてみます.  のなんとか乗は常に正ですから,
これらを満たすのは
のなんとか乗は常に正ですから,
これらを満たすのは 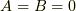 のときのみです.これらを
のときのみです.これらを 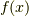 に代入すると
やっぱり
に代入すると
やっぱり 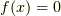 となってしまいます.これを「恒等的にゼロである」といいます.
せっかくさっき
となってしまいます.これを「恒等的にゼロである」といいます.
せっかくさっき 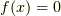 になる解を避けたのに,これでは意味がありません.
になる解を避けたのに,これでは意味がありません.
したがって  が正のときは恒等的にゼロでない解,
つまり非自明解は存在しません.他の場合を調べましょう.
が正のときは恒等的にゼロでない解,
つまり非自明解は存在しません.他の場合を調べましょう.
λ がゼロの場合
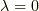 なら 式(6) は
なら 式(6) は
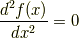
となります.つまり  で2階微分してゼロになるものが
で2階微分してゼロになるものが 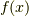 だといっています.
2階微分でゼロになる式はたくさんありますが,一般解は
だといっています.
2階微分でゼロになる式はたくさんありますが,一般解は
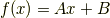
と書けますよね(実際に  で2階微分してみてください.ゼロになるでしょう?).
境界条件
で2階微分してみてください.ゼロになるでしょう?).
境界条件 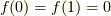 を適用すると
を適用すると
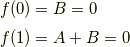
です.これらを満たすのは 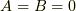 のときなので,またしても非自明解を持ちません.
他の場合を調べます.といっても残りは
のときなので,またしても非自明解を持ちません.
他の場合を調べます.といっても残りは  が負の場合だけなので,今度こそ解があると期待できます.
が負の場合だけなので,今度こそ解があると期待できます.
λ が負の場合
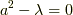 より
より
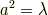
です.ここで  は負なのでそのままルートを付けてはいけません!
は負なのでそのままルートを付けてはいけません!
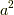 は
は  に等しいから負の値なので,2乗して負になるように
虚数単位
に等しいから負の値なので,2乗して負になるように
虚数単位 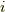 をルートの前につけておきます.
をルートの前につけておきます.  はルートの中にあるので絶対値をつけます.したがって
はルートの中にあるので絶対値をつけます.したがって
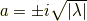
です. 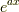 を解として代入したんですから,解は
を解として代入したんですから,解は
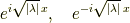
の2つです.一般解はこれらの線形結合で,
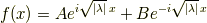
と表されます.  の肩に虚数単位
の肩に虚数単位 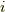 が乗っていますね.オイラーの公式をつかいましょう.
が乗っていますね.オイラーの公式をつかいましょう.
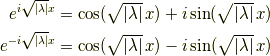
より
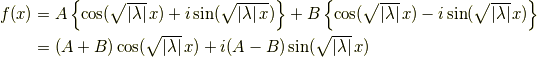
となって,ここで 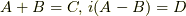 と新しい定数に置き換えると
と新しい定数に置き換えると
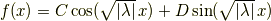
になります.境界条件 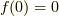 を適用すると
を適用すると
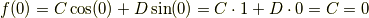
です.したがって 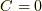 ということが分かったので
ということが分かったので

と書けます.さらに上式に境界条件  を適用すると
を適用すると

ですね. 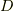 がゼロなら常に
がゼロなら常に 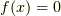 ですから,
解をもつためには
ですから,
解をもつためには  でないといけません.したがって,
でないといけません.したがって,
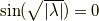
です. 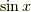 は周期関数で,
は周期関数で, 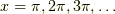 でゼロになります.つまり
でゼロになります.つまり
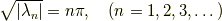
がいえます.ここで  を
を 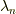 としているのは,
それぞれの
としているのは,
それぞれの  に対応した定数
に対応した定数  がいくつもあることを表しています.
がいくつもあることを表しています.
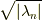 が分かったので
が分かったので 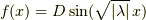 は
は
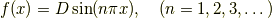
となりますが,  を
を 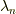 にしたのと同様に,
それぞれの
にしたのと同様に,
それぞれの  に対応する
に対応する 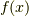 と
と 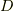 も多数存在するので,
も多数存在するので,
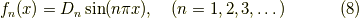
と書いておきます.やれやれ,ちょっと疲れましたがやっと境界条件を満たす 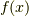 の解が求まりました.
の解が求まりました.
もう1つの常微分方程式を解く
最初に変数分離したとき,二つの常微分方程式に分かれました. そのうち一つはさっき考えたので,今度はもう一方の常微分方程 式(4) を考えます. 式(4) は少し変形すると

です. 式(5) が境界条件を満たす解を先ほど求めたので,それに対応する解を求めます.
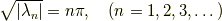
の両辺を2乗すると

で,  は負だったので
は負だったので
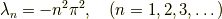
です.これを 式(9) に代入すると
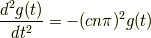
となります.解として 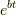 を代入すると
を代入すると
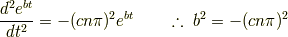
ここで 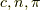 はいずれも正ですから
はいずれも正ですから
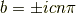
です.したがって解(特解)は
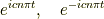
の2つで,一般解はこれらの線型結合で

と書けます.例によってオイラーの公式で展開して整理すると
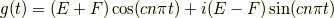
さらに 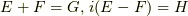 と置くと
と置くと
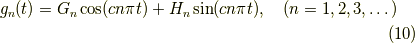
となります.
2つの常微分方程式を合わせる
さて,境界条件を考えることで変数分離した常微分方程式のそれぞれの解が分かりました.再掲すると
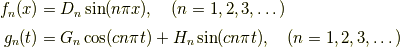
です. 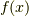 と
と 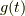 はもともと波動方程 式(1) を変数分離するため
に
はもともと波動方程 式(1) を変数分離するため
に 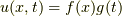 とおいたものでした.したがって
とおいたものでした.したがって
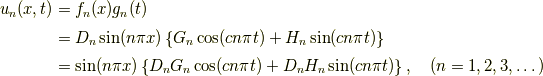
です.ここで 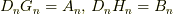 とおきます
(
とおきます
( 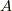 と
と 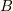 は最初の方で使いましたが,ここでは新しい定数として使います).
さらに
は最初の方で使いましたが,ここでは新しい定数として使います).
さらに  とおきます.すると
とおきます.すると
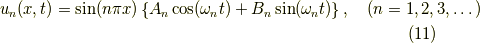
初期条件を考える
境界条件を満たす解が分かりましたから,あとは初期条件を満たすようにするだけです.
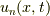 はいろいろな
はいろいろな  に対する解がたくさんありますが,
重ね合わせの原理よりそれらすべてを足したもの(線型結合)も解となります.すなわち
に対する解がたくさんありますが,
重ね合わせの原理よりそれらすべてを足したもの(線型結合)も解となります.すなわち
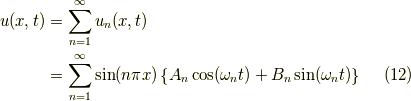
です.初期条件  を当てはめるため,
まず
を当てはめるため,
まず 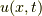 を
を  で偏微分しておきましょう.
で偏微分しておきましょう.
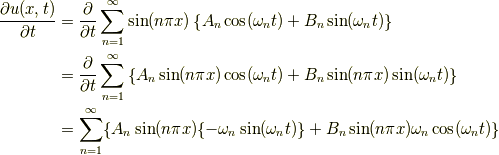
そして上式に  を適用すると
を適用すると
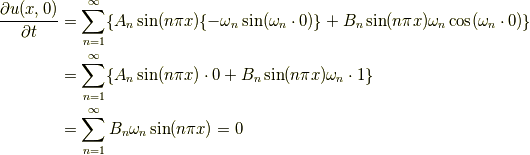
となります.また,もう一つの初期条件 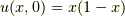 より
より
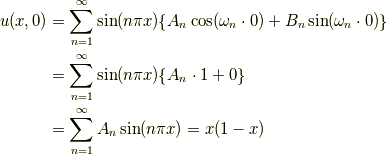
です.まとめると
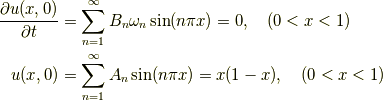
となります(  の範囲 (
の範囲 (  ) はもともとの波動方程式のものです).
これはフーリエ正弦級数の形をしています.したがって 式(12) が初期条件を満たすため
には
) はもともとの波動方程式のものです).
これはフーリエ正弦級数の形をしています.したがって 式(12) が初期条件を満たすため
には  は 0 の半区間でのフーリエ正弦級数,
は 0 の半区間でのフーリエ正弦級数,  は
は  の半区間でのフーリエ正弦級数でなければならないので,フーリエ級数の公式から
の半区間でのフーリエ正弦級数でなければならないので,フーリエ級数の公式から
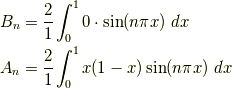
となり,
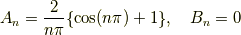
が得られます.こうして係数  と
と  が決まったので,
これらを 式(12) に代入すれば境界条件と初期条件を満たす1次元波動方程式の解
が決まったので,
これらを 式(12) に代入すれば境界条件と初期条件を満たす1次元波動方程式の解
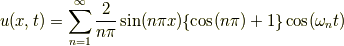
が得られます.これでようやく解けました.お疲れさまです.