この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
gradの座標変換
ベクトル解析で出てくるgrad(グラディエント,勾配)は, 他のデカルト座標系では果たして本当にベクトルとして振舞うのかを 調べてみました.
前の記事は, rotの座標変換 です.
基本的なこと
これから,座標の変換を議論します.そこで, rotの座標変換 で用いたのと同じ変換行列 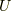 を用います.
を用います.
つまり,座標系 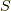 のベクトル
のベクトル 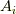 と座標系
と座標系 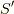 のベクトル
のベクトル 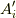 について,
実直交行列
について,
実直交行列 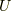 が存在して,次のように表わされます.
が存在して,次のように表わされます.
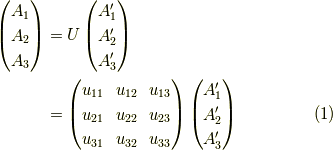
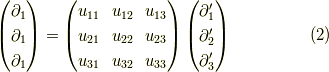
今回は,
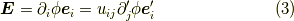
を示せば良いことになります.
成分で示せば,
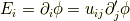
第一成分,つまり  成分の変換をみます.
成分の変換をみます.
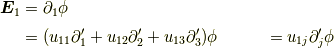
第二成分,第三成分にも同じことが言えます. よって,確かにgradはベクトルとして振舞うことが分かります.
これで,めでたくdiv,rot,gradの全てが座標変換でスカラーやベクトルとして 振舞うことが示せました.よかった,よかった^^
それでは,今日はここまで.