この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
dx/dtをdxとdtに分けて良いの?
短い記事です.積分をする時に 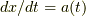 を
を 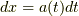 として,
として, 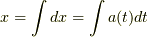 としますが,
少なくとも僕は最初とまどいました.
不思議な事に
としますが,
少なくとも僕は最初とまどいました.
不思議な事に 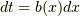 としても同じ結果が得られます.
それの根拠を探ります.
としても同じ結果が得られます.
それの根拠を探ります.
この記事ではこれを一般化して,

と,

の同値性を示します.
本題
まず,式 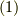 から式
から式 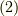 を導きます.
前提として,鎖の規則と逆関数の微分法を認めます.
を導きます.
前提として,鎖の規則と逆関数の微分法を認めます.
準備として 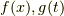 の原始関数の一つを
の原始関数の一つを 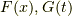 ,積分定数
,積分定数 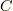 として,
として,
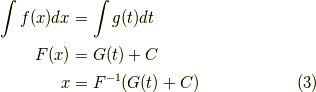
となります.ここで,式 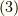 の最終行の両辺を
の最終行の両辺を 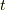 で微分します.
で微分します.
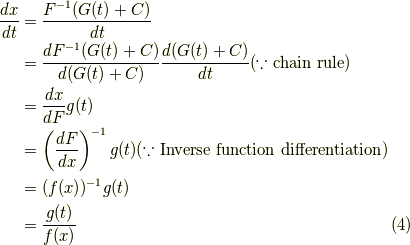
こうして,式 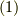 から式
から式 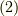 が導けました.
そして,逆をたどれば式
が導けました.
そして,逆をたどれば式 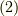 から式
から式 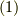 を導けます.
を導けます.
よって,鎖の規則と逆関数の微分法を認めることで,
式 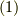 と式
と式 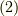 は同値なものであると分かりました.
は同値なものであると分かりました.
今日はこの辺で,お疲れさまでした.