この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
斜交座標での2次元フーリエ変換
二次元フーリエ変換ってありますよね.僕が今まで見たことあるものは, 全て2つの変数が直交したものでした.そこで,今回2つの変数が斜交座標を なしている時のフーリエ変換を考えます.
この記事の結論から書くと,
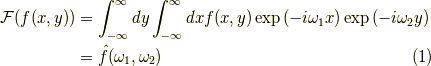
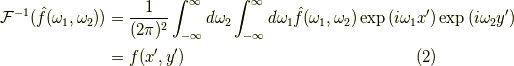
に対して,次の  で斜交座標系でのフーリエ変換を定義すると,
で斜交座標系でのフーリエ変換を定義すると,
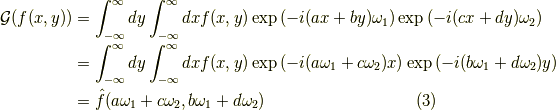
と,普通の二次元フーリエ変換の波数 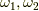 がそれぞれ
がそれぞれ 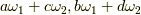 で置き換えられたものとなり,更に逆変換は次のようになります.
で置き換えられたものとなり,更に逆変換は次のようになります.
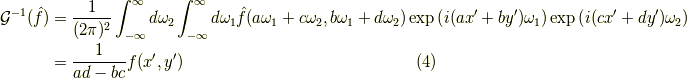
が成立します.
証明
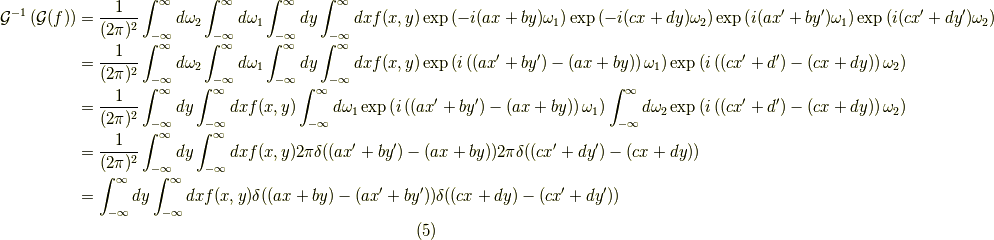
ここで,
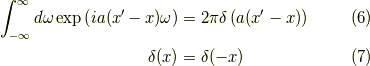
を用いました.さて,ここで
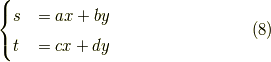
と置きます.すると,
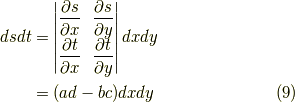
です.つまり,

を使って,
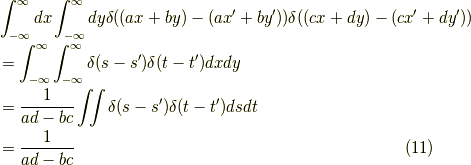
ですから,
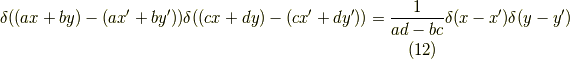
となります.よって,
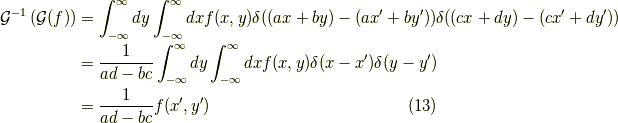
が言えました.この積分の微小要素  は符号付きで
あります.
は符号付きで
あります.  方向を反時計周りに90度回転すると
方向を反時計周りに90度回転すると  方向となる.
この時積分素
方向となる.
この時積分素 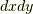 は正になります.
は正になります. 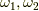 についても同様です.
についても同様です.
また,波面に垂直なベクトル 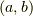 を
を 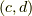 に原点を中心に回転して
方向を重ねる時,
反時計回りに回った方が早い場合,
に原点を中心に回転して
方向を重ねる時,
反時計回りに回った方が早い場合,  であり,
時計回りに回った方が早い場合,
であり,
時計回りに回った方が早い場合, 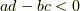 です.
なお,この
です.
なお,この 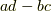 とはベクトル
とはベクトル 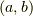 と
と 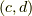 から作られる平行四辺形の面積の事です.
から作られる平行四辺形の面積の事です.
今回ここで示した定理は不思議な事だと思うのです. 直交した2方向のフーリエ変換と斜交した2方向のフーリエ変換は 波数空間では少し違ったものになりますが, もう一度フーリエ逆変換を施すと,定数倍の差こそあれ, 元の関数に戻ってくるのです.最初に試みた時は, 複雑な計算になってしまうだろうと思っていましたが, 実際やってみると,すごく簡単でした.
ここで示せたことを簡単に言葉で解釈するなら,
今までの二次元フーリエ変換では,二次元の関数を 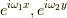 の基本的な波(基底)に分解していましたが,実は,
の基本的な波(基底)に分解していましたが,実は, 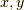 の様には直交していない基本的な波(基底)
の様には直交していない基本的な波(基底) 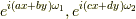 でも,定数倍の差こそあれ,きちんと表現できるという事です.
でも,定数倍の差こそあれ,きちんと表現できるという事です.
今日はこの辺で,お疲れ様でした.