この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。リンクを正しく張れていないところが存在しますのでご注意ください。正式公開まで、いましばらくお待ちください。
grad

微分演算子をベクトルに組み合わせたナブラというベクトル演算子を定義しました．ナブラは次のように書けます．

$\nabla =\left( \frac{\partial }{\partial x_{1}}, \ \frac{\partial }{\partial x_{2}}, \ \frac{\partial }{\partial x_{3}} \right)$

ナブラをスカラーに作用させたものを grad とも書くのでした．（ナブラをベクトルに作用させるときは 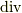${\rm div}$ と書きます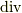． ${\rm div}$ はまた後で勉強します．）この記事では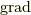， ${\rm grad}$ について考察してみます．

[*]

ナブラはハミルトンの演算子と呼ばれることもありますが，最初にこの記号を考案し，数学的に発展させたのはハミルトンの弟子のテイト( $\text{Peter Gurthrie Tait (1831-1901)}$ )です．（一番最初は横向きに $\triangleleft$ と書いたようです．）電磁気学のマックスウェルは，はっきりとテイトの業績を讃えていますが，現代でもいまいちテイトの名前はハミルトンの陰に隠れています．もっとも，最初期の $\nabla$ には，まだ四元数の理論の影響が強く，人によって符号などが統一されていませんでした．テイトは非常に広汎な研究を進めたにも関わらず，四元数を離れてベクトルだけ使うという思考の変換が果たせず，ナブラを電磁気学に本格的に用いはじめたギブス( $\text{Josiah Willard Gibbs (1839-1903)}$ )やヘヴィサイド( $\text{Oliver Heaviside (1850-1925)}$ )を批判して激論を繰り広げています．しかし，その後のベクトル解析分野は，電磁気学の進歩に伴い，ギブスやヘヴィサイドなどの電磁気学者によって大きく発展させられていきます．この記号をデル，アトレッドまたはエイトレッドなどと呼ぶ人もいるようです．これは $\nabla$ が逆三角形なので，記号 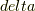delta

を逆から読んでのことだそうです．しゃれた名前ですが，アトレッドと呼んでいる人を見たことはありません．

古代アッシリアの竪琴，Nebel.この楽器の形に似ていることにNablaの名前は由来する．旧約聖書にも出て来る楽器だ．

方向微係数の最大値

方向微分は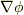， $\nabla \phi$ と方向ベクトル 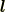$\bm{l}$ を使って次のように定義されました．

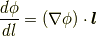
$\frac{d\phi}{dl}= (\nabla \phi ) \cdot \bm{l}$

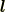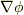方向微係数は， $\bm{l}$ と $\nabla \phi$ が同じ方向を向いている時に最大値を取ります．

[†]	スカラー場の勾配のイメージは，ベクトル解析奮闘記１を参照下さい．方向微係数が最大値となる向きとは，同記事の挿絵で，汗を流して人が登っている，傾斜が最大の向きです．

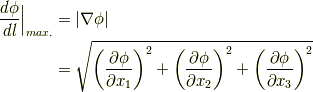
$\frac{d\phi}{dl} \Big| _{max.} &= | \nabla \phi | \\& = \sqrt{ \left( \frac{\partial \phi}{\partial x_{1}} \right) ^{2} + \left( \frac{\partial \phi}{\partial x_{2}} \right) ^{2} +\left( \frac{\partial \phi}{\partial x_{3}} \right) ^{2} }$

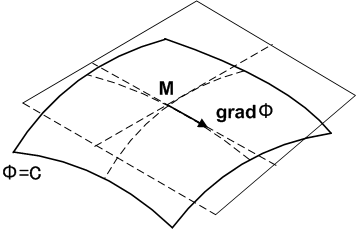
gradΦのイメージ

スカラー場 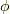$\phi$ に対し，等位面 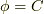$\phi = C$ を考え，その任意の一点を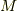とするとき，ベクトル 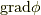${\rm grad} \phi$ は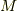，における接平面に含まれます．

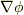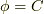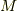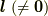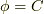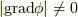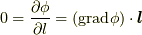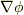すんなりと $\nabla \phi$ が法線ベクトルになっていることが分かる人は，それでいいです．パッと分からない人は，以下のように考えて確認してみましょう．等位面 $\phi = C$ と，点の接平面に含まれるベクトル $\bm{l} \ (\ne \bm{0})$ を考えます．このとき， $\phi = C$ より $\frac{\partial \phi }{\partial l} = 0$ ですが，一般には $|{\rm grad }\phi | \ne 0$ のはずです．そこで定義 $0= \frac{\partial \phi }{\partial l} =({\rm grad} \phi) \cdot \bm{l}$ より， $({\rm grad} \phi) \perp \bm{l}$ が要請されるわけです．そこで， $\nabla \phi$ は等位面に直交する向き，つまり法線方向を向いていることが分かります．

この結果を次のように応用することも出来ます．等位面 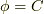$\phi = C$ の単位法線ベクトルを 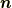$\bm{n}$ とすると，次のような式変形が可能です．

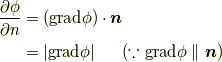
$\frac{\partial \phi }{\partial n} & =({\rm grad} \phi) \cdot \bm{n} \\ & = |{\rm grad} \phi| \ \ \ \ \ (\because {\rm grad} \phi \parallel \bm{n})$

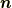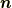もしくはベクトル形で ${\rm grad}\phi =\frac{\partial \phi }{\partial n}\bm{n}$ と表現できます．これが，法線ベクトルを使った勾配の表現となります．『曲面の単位法線 $\bm{n}$ を求めよ』という問題に対しては，逆に $\nabla$ を用いて $\bm{n}$ を表現することが出来ます．

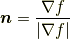
$\bm{n} = \frac{\nabla f}{|\nabla f|}$

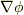[‡]	$\nabla \phi$ を表現するのに，ガウスの積分定理という定理を用いる方法もあります． gradの積分形による定義で紹介します．

接平面の表現

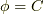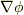前セクションの結果を用いると，スカラー関数の等位面 $\phi=C$ の接平面を $\nabla \phi$ を用いて表わすことができます．幾何学の問題に御利用ください．一般に，陰関数 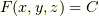F(x,y,z)=C の形で曲面の方程式が与えられているとき，ある点 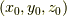$(x_{0},y_{0},z_{0})$ における法線ベクトルは 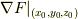$\nabla F|_{(x_{0},y_{0},z_{0})}$ で与えられます．この点における接平面の方程式は，法線ベクトルに直交し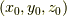， $(x_{0},y_{0},z_{0})$ を通るベクトルとして表現されますので，ベクトルの内積を用いて次のように書けるでしょう．

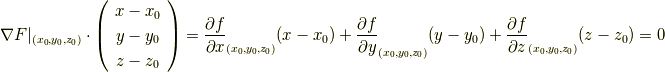
$\nabla F|_{(x_{0},y_{0},z_{0})} \cdot \left( \begin{array}{c}x-x_{0} \\ y-y_{0} \\z-z_{0} \\ \end{array}\right)=\frac{\partial f}{\partial x}_{(x_{0},y_{0},z_{0})}(x-x_{0})+\frac{\partial f}{\partial y}_{(x_{0},y_{0},z_{0})}(y-y_{0})+\frac{\partial f}{\partial z}_{(x_{0},y_{0},z_{0})}(z-z_{0})=0$

勾配の演算

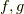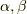関数の勾配を取る場合，次のような演算法則がなりたちます．普通の微分演算でなりたつ算法と同じですね．（ f,g 等は関数， $\alpha , \beta$ 等はスカラーとします．）

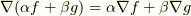
$\nabla (\alpha f + \beta g)= \alpha \nabla f + \beta \nabla g$
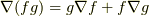
$\nabla (fg)= g \nabla f + f \nabla g$
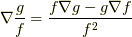$\nabla \frac{g}{f}= \frac{f \nabla g - g \nabla f}{f^{2}}$ （商の微分）
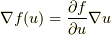$\nabla f(u)= \frac{\partial f}{\partial u}\nabla u$ （合成関数の微分）
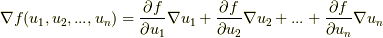$\nabla f(u_{1},u_{2},...,u_{n})= \frac{\partial f}{\partial u_{1}}\nabla u_{1}+\frac{\partial f}{\partial u_{2}}\nabla u_{2}+...+\frac{\partial f}{\partial u_{n}}\nabla u_{n}$ （チェーン・ルール）

[§]	一番目の性質は，ナブラが線形性を持つことを示しています．このような演算子を線形演算子と呼びます．線形演算子の性質は線形ですから，線形演算子の性質を考える際には線形代数の成果を応用することができます．この先，色々な線形演算子が出て来ると思いますが，線形代数の知識（具体的にはベクトルや行列）を応用するような場合もあるでしょう．いずれ，行列の固有値のように，線形演算子の固有値や固有ベクトルといった問題も出て来ると思います．微積分の計算と線形代数は，最初は別々に勉強しますが，そろそろ融合してきます．楽しみですね．

[home] [ベクトル解析] [ページの先頭]