この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
ハミルトニアンの非対角成分の意味
この記事では,二次エルミート行列であるハミルトニアンを例にとって, ハミルトニアンの非対角成分の意味を調べます.
シュレーディンガー方程式は時間発展の記述を可能にする
系が持つハミルトニアンからは系の時間発展が分かります. なお,ハミルトニアンは時間依存性が無いものとします. まず,波動関数は以下のようであるとします.

さて,その主張の根拠はシュレディンガー方程式にあります. つまり,

ですね.これを少し変形します.
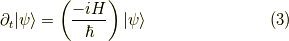
ここで  の時間依存性をあらわに
表して,
の時間依存性をあらわに
表して,  と書く事にします.
すると,テイラー展開から,
と書く事にします.
すると,テイラー展開から,
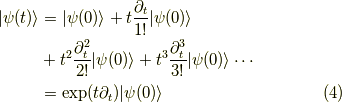
となります.ちなみに上の  のべきは
のべきは  に対して定数であり,
に対して定数であり, 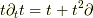 等の考慮は不要です.テイラー展開とはそういうものです.よって,式
等の考慮は不要です.テイラー展開とはそういうものです.よって,式 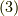 からこのテイラー展開はハミルトニアンの指数関数(行列の指数関数)で表されます.よって,
からこのテイラー展開はハミルトニアンの指数関数(行列の指数関数)で表されます.よって,
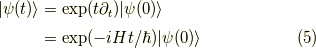
となります.これから,話したいことは, 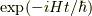 を求める事です.
ハミルトニアンはエルミート演算子ですから,時間依存しない二次正方行列なら以下の形で
一般的なものになります.
を求める事です.
ハミルトニアンはエルミート演算子ですから,時間依存しない二次正方行列なら以下の形で
一般的なものになります. 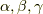 は実数です.
パウリ行列を特に意図していない事だけ注意しておきます.
は実数です.
パウリ行列を特に意図していない事だけ注意しておきます.
行列の指数関数の計算
さて,  を求めるにはまず対角化します.
固有値方程式は以下です.
を求めるにはまず対角化します.
固有値方程式は以下です.
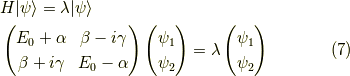
ここで,  は
は  と同じ事ですから,変形して
と同じ事ですから,変形して
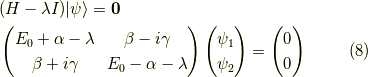
となります.ここで, 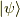 が恒等的にゼロでなくなり,
非自明解が存在する条件は,二次行列の行列式がゼロになる時ですから,
が恒等的にゼロでなくなり,
非自明解が存在する条件は,二次行列の行列式がゼロになる時ですから,
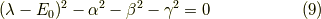
よって,

とおくと,  は二通りあって,
は二通りあって,

(ただし,複号同順)となります.
ここで,それぞれの固有ベクトルを求める
と, 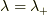 の時,
の時, 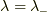 の時,それぞれ,
の時,それぞれ,
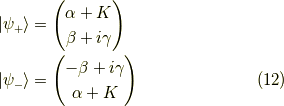
となります.よって,その二つを並べた二次正方行列  とすると,
とすると,

であり,その行列式を  とすると,
とすると,

であり,逆行列は
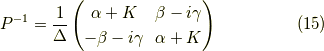
となりますから,対角化は以下のように実行できます.
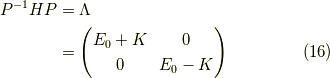
この形になれば,行列の指数関数は簡単に求まって,
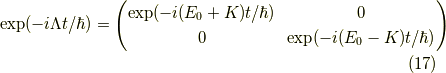
となります.ここまで来たら,行列の任意の関数  について,
について,
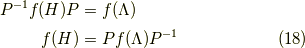
ですから, 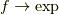 として,
として,
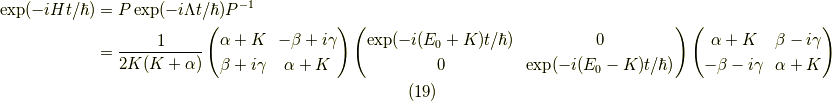
ここで, 行列の三連続積の展開 を用いて,
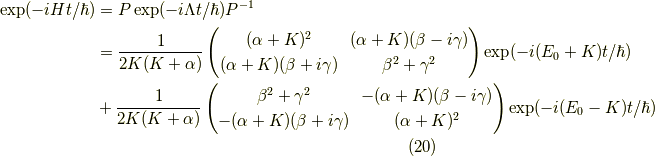
これが一般的な式です.これからは特殊な場合を二通り考えてみようと思います.
(1) α = 0 の時
まずは, 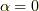 の時です,ハミルトニアンの対角成分が等しい時ですね.
この時,
の時です,ハミルトニアンの対角成分が等しい時ですね.
この時,
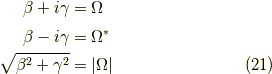
と置くと,

となります.例えば,波動関数の初期状態が純粋な状態,
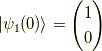
だった時には,
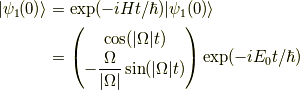
の様に正弦・余弦波的な振る舞いをすると分かります.
さらには 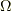 の絶対値が小さい時には,
振動はゆっくりで
の絶対値が小さい時には,
振動はゆっくりで 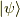 の第一成分と第二成分の行き来がゆっくりなのに対して,
絶対値が大きいと成分は激しく入れ替わります.この様に,
ハミルトニアンの非対角成分は状態間の混じり方や相互作用の強さに関係すると分かります.
の第一成分と第二成分の行き来がゆっくりなのに対して,
絶対値が大きいと成分は激しく入れ替わります.この様に,
ハミルトニアンの非対角成分は状態間の混じり方や相互作用の強さに関係すると分かります.
(2) β = γ = 0 の時
今度は 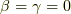 の時です.
この場合は,
の時です.
この場合は,
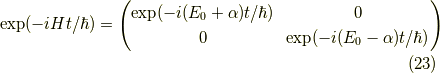
状態は位相の変化以外は変化がなく,二成分間の行き来は無いことが分かります.
おまけ
なお,  と置いた時には,
波動関数の運動方程式,
と置いた時には,
波動関数の運動方程式,
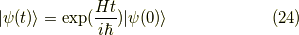
は,左から 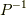 を掛けて,
を掛けて, 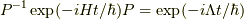 を用いれば,
を用いれば,
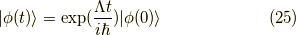
とも,表せます.状態ベクトルがきれいになるか,ハミルトニアンがきれいになるか, トレードオフと云う訳です.
以上で,話は終了です. 今日はここまで,お疲れ様でした.