この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
ベクトル場から積分曲線を求める方法
この記事では,拙記事 微分幾何学における流れの具体例 を書いた時点では不明だった 積分曲線を求める方法を書きます.
前記事における例5
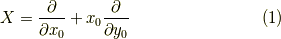
から
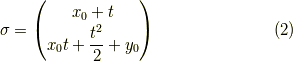
を求めたい訳です. 結論から言うと,地道に連立微分方程式を解くことで解は得られます. どの本にも載っていない気がしたのですが,ふたを開けてみればそういうことでした.
早速やってみましょう.
積分曲線 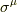 を次の様に置きます.
を次の様に置きます.
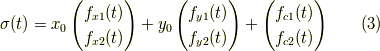
そして,この初期条件は

となります.
すると,ベクトル場を計算すると, 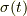 に
に 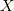 を作用させればよく,
を作用させればよく,
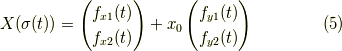
です.積分曲線とは,

を満たす曲線の事なので, 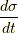 を計算すると,
を計算すると,
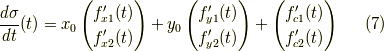
式 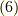 の両辺を比較すると,
の両辺を比較すると,
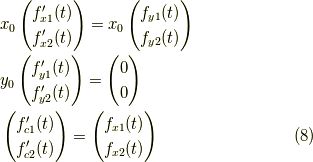
まず, 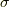 の
の  成分から求めましょう.上段の事です.
成分から求めましょう.上段の事です.
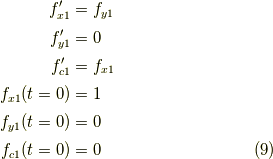
まず,二番目の式から,

一番目から,

最後に,

次に下段です.
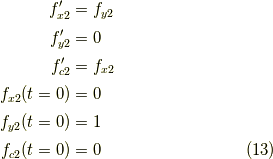
同様に解くと,

よって,素材が揃ったので 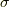 を求めると,
を求めると,
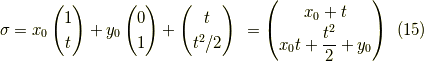
となり,無事求められました. 今日はここまで.お疲れさまでした!