この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
スピン軌道相互作用
今回は要点を押さえていないと,理解が難しいと思われる スピン軌道相互作用について解説します.
LS多重項
まずは,LS多重項について考えましょう.原子核の周りには軌道があります.
例えば, 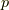 軌道は
軌道は 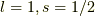 を持ちます.
を持ちます. 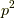 状態
(
状態
( 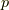 軌道に二つ電子が詰まった状態)について考えます.
軌道に二つ電子が詰まった状態)について考えます.
すると,軌道に関しては 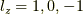 の三通り,それぞれにスピンは
の三通り,それぞれにスピンは 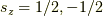 の二通りありますから,結局,軌道は
の二通りありますから,結局,軌道は 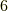 種類あります.
種類あります. 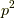 状態はそこから,
状態はそこから, 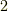 つを選ぶので,
15通りあることになります.電子の入る二つの軌道を
つを選ぶので,
15通りあることになります.電子の入る二つの軌道を 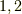 とし(電子は区別できない
ので,
とし(電子は区別できない
ので, 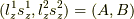 と
と 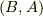 は同じものです.),
は同じものです.),  と
と  を
それぞれ「合成軌道角運動量」と「合成スピン角運動量」の
を
それぞれ「合成軌道角運動量」と「合成スピン角運動量」の  成分として,列挙すると,
成分として,列挙すると,
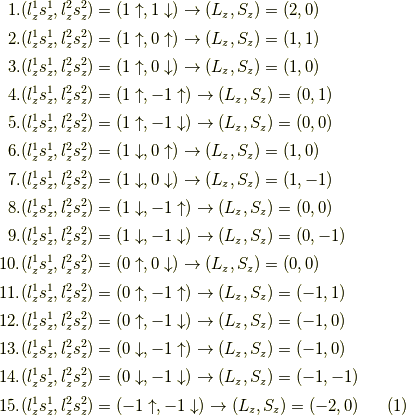
これらの線形結合で, 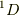 の5個,
の5個, 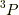 の9個,
の9個, 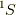 の1個が表されます.
この記法では,
の1個が表されます.
この記法では, 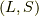 をラベルするのに
をラベルするのに 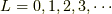 は中心の文字として
は中心の文字として 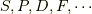 と表し,
スピンは左肩に
と表し,
スピンは左肩に 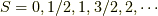 に対して,
に対して, 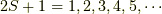 (つまり,取れる
(つまり,取れる 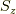 状態の数が
状態の数が 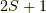 個)と
書いて,
個)と
書いて, 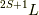 と書いたのです.
と書いたのです.
つまり, 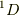 は
は 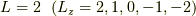 で
で 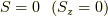 の
5状態,
の
5状態, 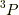 は
は 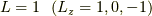 で
で 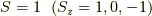 の
9状態,
の
9状態, 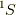 は
は 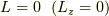 で
で 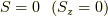 の
1状態を表します.
の
1状態を表します.
注意することは, 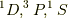 に含まれる15状態は,
直接式
に含まれる15状態は,
直接式 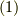 と対応しておらず,同じ
と対応しておらず,同じ 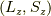 を持つ状態の「線形結合」で混合されている状態
になっているということです.この辺の事情は詳しくは拙記事 LS多重項 をご覧ください.
を持つ状態の「線形結合」で混合されている状態
になっているということです.この辺の事情は詳しくは拙記事 LS多重項 をご覧ください.
この 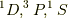 の状態の内最もエネルギーの小さいものはどれになるか?
それにこたえるのが,次小節「フントの規則」です.
の状態の内最もエネルギーの小さいものはどれになるか?
それにこたえるのが,次小節「フントの規則」です.
フントの規則
さて,LS多重項の最低エネルギーを見つける経験則がフントの規則と言われ,
(第一優先) まず,全スピン 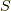 を最大にする
を最大にする
(第二優先) 次に全軌道角運動量 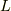 を最大にする
を最大にする
となります.この場合,スピンが最大のものが第一優先ですから, 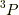 がスピン最大
がスピン最大 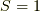 となり,
これが最低エネルギーのLS多重項となります.
となり,
これが最低エネルギーのLS多重項となります.
スピン軌道相互作用
ここで衝撃的な事実を発表します.1つの軌道に1電子を入れる場合, 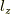 と
と 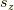 は反対向きの時が一番エネルギーが低いのです..あれ?なんかこれ,フントの規則と矛盾していませんか?
は反対向きの時が一番エネルギーが低いのです..あれ?なんかこれ,フントの規則と矛盾していませんか?
安心してください.これは矛盾しません.フントの規則を1粒子に制限すると,  :最大の内の
:最大の内の 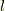 :最大の時が最もエネルギーが低いです.そう,フントの規則では軌道角運動量とスピンの「大きさ」(S,L)について述べているのに対して,この小節の最初に言ったことは,軌道角運動量とスピンの「z成分」(S_z,L_z)が反対向きの時が一番エネルギーが低いと言っているのです.
:最大の時が最もエネルギーが低いです.そう,フントの規則では軌道角運動量とスピンの「大きさ」(S,L)について述べているのに対して,この小節の最初に言ったことは,軌道角運動量とスピンの「z成分」(S_z,L_z)が反対向きの時が一番エネルギーが低いと言っているのです.
ということはです.フントの規則で決めたLS多重項はさらに軌道角運動量 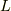 とスピン角運動量
とスピン角運動量 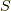 の相対的な向きで,エネルギーが変わってくるということです.そのスピンと軌道の向きの変化からくるエネルギーの変化を「スピン軌道相互作用」
の相対的な向きで,エネルギーが変わってくるということです.そのスピンと軌道の向きの変化からくるエネルギーの変化を「スピン軌道相互作用」 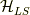 と呼びます.
と呼びます. 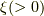 を原子には依るが,軌道に入る電子には依らない(
を原子には依るが,軌道に入る電子には依らない( 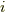 には依らない)量として,
には依らない)量として,
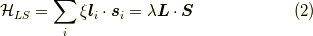
何気なく 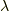 と書きましたが,これは
と書きましたが,これは 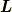 と
と 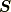 が同じもの同士な時のみ比較できる値になります.
つまり,
が同じもの同士な時のみ比較できる値になります.
つまり, 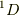 の5状態内の比較なら
の5状態内の比較なら 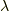 は意味を持ちますが,
は意味を持ちますが, 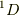 と
と 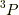 の比較を一つの
の比較を一つの 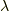 では出来ません.
では出来ません.
今,二つのベクトルの内どちらかの向きに  軸を取ることにします.すると,内積は
軸を取ることにします.すると,内積は  成分のみで書けます.つまり,
成分のみで書けます.つまり,
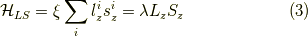
と考えやすくなります.
d軌道についてのスピン軌道相互作用
さて,具体例で考えましょう. 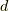 軌道に
軌道に 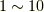 個の電子を詰めていって,
個の電子を詰めていって, 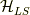 を求めます.
その際の電子の詰め方は,フントの規則に従います.LS多重項内での最低エネルギーの
を求めます.
その際の電子の詰め方は,フントの規則に従います.LS多重項内での最低エネルギーの 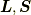 を持つ状態達を考え,そこにスピン軌道相互作用が引き起こすエネルギーの向き関係依存性を調べて,その中でもさらに低いエネルギーを考えるのです.この同じLS多重項内で一番低いエネルギーの状態をJ多重項と言います.
を持つ状態達を考え,そこにスピン軌道相互作用が引き起こすエネルギーの向き関係依存性を調べて,その中でもさらに低いエネルギーを考えるのです.この同じLS多重項内で一番低いエネルギーの状態をJ多重項と言います.
参考までに,詰めていく途中で下のような状態を経ることを図にしておきます.
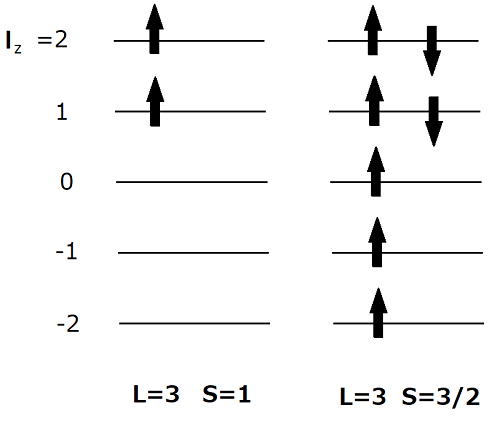
図1:軌道に電子をフントの規則に従って詰めていく
実際,詰めていきましょう.まず,1つ目の電子
は,  のそれぞれに対し,
のそれぞれに対し,  があり得るわけですが,
があり得るわけですが, 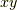 平面対称なので,ここでは専ら
平面対称なので,ここでは専ら 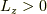 を考えます.
を考えます.
式 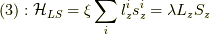 より,
より,
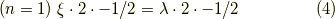
よって,1つの電子( 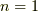 )の時,
)の時,

同様に 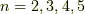 までは,
までは,
式 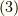 の中辺は,
の中辺は,
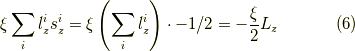
一方,式 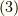 の右辺は,
の右辺は,

これらが等しいので,

が言えます.実際の計算は,図1の順番で
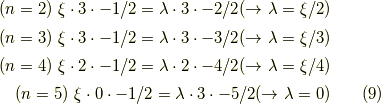
そして,更に  だと,
だと,
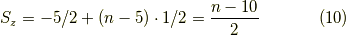
となりますから,
式 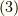 の中辺は,
の中辺は,
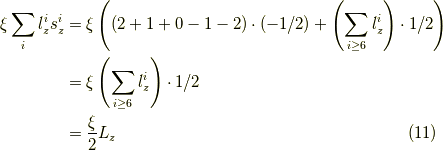
一方,式 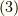 の右辺は,
の右辺は,
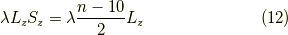
これらが等しいので,

が言えます.
実際書いてみると,
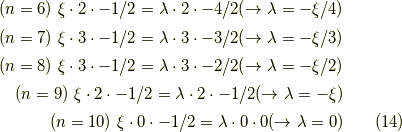
となります.
まとめると,
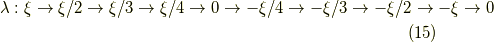
と変化します.
J多重項と最低エネルギー
面白いのはここからです. 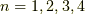 の時,
の時,  ですから,
軌道角運動量とスピンは反平行(真逆の向き)で最低エネルギーを取ります.
よって
ですから,
軌道角運動量とスピンは反平行(真逆の向き)で最低エネルギーを取ります.
よって 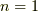 は,
は, 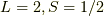 だから,
だから, 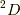 までは確定です.
さらにもっとも反平行に近い角運動量の位置は,
までは確定です.
さらにもっとも反平行に近い角運動量の位置は, 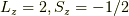 ですから,
ですから,
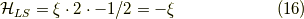
となります.この時,ベクトルの足し算

で全角運動量 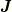 を導入します.ここで,その大きさ
を導入します.ここで,その大きさ 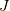 は
は
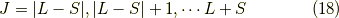
を取ります.フントの規則に従った最低エネルギー状態,LS多重項を 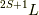 と書いたようにスピン軌道相互作用で分裂した状態の最低エネルギー状態をJ多重項と言い,
と書いたようにスピン軌道相互作用で分裂した状態の最低エネルギー状態をJ多重項と言い, 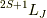 と書きます.
と書きます.
今,つまり 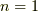 の時は,
の時は, 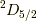 ,
, 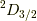 があるわけです.
一番反平行なのは,
があるわけです.
一番反平行なのは, 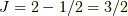 だから,
だから, 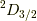 です.
です.
次に 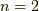 の時です.
の時です. 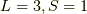 で
で 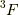 が確定.(ここで注意して欲しいことは,
が確定.(ここで注意して欲しいことは, 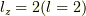 と,
と, 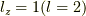 の合成の内,合成軌道角運動量の「z成分」
の合成の内,合成軌道角運動量の「z成分」 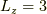 が最大ですが,その場合,合成軌道角運動量の「大きさ」
が最大ですが,その場合,合成軌道角運動量の「大きさ」 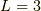 が言えるようです.(参考文献 p.14 参照) )
さっき同様に取れる
が言えるようです.(参考文献 p.14 参照) )
さっき同様に取れる 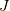 は
は 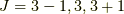 より,
より, 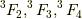 があるうち,
一番反平行なのは,
があるうち,
一番反平行なのは, 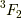 です.
です.
この時,
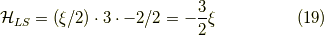
となります.同様に式 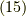 の方式でJ多重項と
の方式でJ多重項と 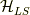 を書くと,
を書くと, 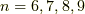 では平行が最低エネルギー(
では平行が最低エネルギー( 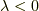 )だったのに気を付けて,
)だったのに気を付けて,
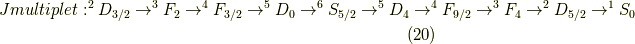
で,
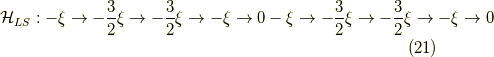
となります.文字通りスピン軌道相互作用とは,全スピンと全軌道角運動量の間の相互作用だったということは納得していただけましたでしょうか? 今日はこの辺で,お疲れさまでした!