この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
標本化定理
ある関数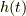 
を，フーリエ変換やフーリエ級数を使って，周波数関数 
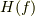で再現するには，いったいどれくらいの範囲の周波数 
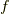の成分が必要になるんでしょうか？逆に，使える周波数成分の範囲が決まっているとき，どのような関数なら再現できるのでしょうか？？この問題は，工学上，とても重要なことです．なぜなら，どれくらいの周波数(周期)成分を使えば，どのような情報が記録できるのかが，この制限から決まってくるからです．
標本化って何？？
当たり前の話ですが，私たちが普段生活しているこの世界は，「ビデオのコマ送りのように，時が途切れ途切れに流れている」とは普通は考えません．途切れていない，連続な世界なのです．しかし，そんな連続な世界で起こっている何かを，データとして記録したいときは，途切れ途切れな時間の間隔で連続な時間を区切って，データを記録します．ちょうど，コマ撮りの写真のように，です．
このように，途切れ途切れの時間または空間の間隔で，連続な世界を区切ることを 標本化する (サンプリングする)といいます．
//画像を載せる予定．
標本化定理
冒頭に書いた問題の答えを出してくれるのが， 
(サンプリング定理)と呼ばれるものです．まだ，「こんな定理の名前なんて初めて聞いた！」という方には，使える周波数の範囲が正しくないと，関数が正しく再現できないということも，イメージがあまり掴めないと思います．このイメージに関しては，後のセクションで実際に例を出していますので，このセクションでは「標本化定理とやらを守っていれば，フーリエ級数を使って関数を完全に再現できるんだ」ということだけ，納得しておいてください．
さて，本題に入りましょう．標本化という言葉を使って，冒頭の問題をもう一度確認してみると，「連続な関数 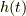をどのくらいの間隔(周期や周波数)で標本化すれば，もとの 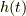を完全に再現できるのだろうか？」ということですね．
そして，以下が標本化定理です．
theorem
ある関数 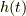を周波数関数 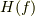で再現するためには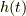， に含まれる最大周波数 
の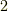 
倍以上の周波数成分を 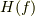が含んでいなければいけない．
上の定理を周期についても，言ってみましょう．つまり･･･
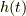ある関数 を周期関数 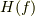で再現するためには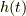， に含まれる最小周期 
の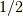 
倍以下の周期成分を 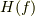が含んでいなければいけない．
ということです．
