この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
像と逆像による保存と劣化
この記事では,写像 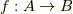 がある時,
がある時, 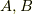 のそれぞれの部分集合を
のそれぞれの部分集合を 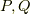 として,
像
として,
像  と逆像
と逆像 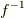 の
の

と言う性質を全射と単射を関連させて,調べます.参考文献は,松坂和夫先生の集合・位相入門です. これは数学の証明の手法がどんなものなのかの一角をよく見て取れる話だと思います.
像と逆像
写像  の定義は,集合
の定義は,集合 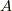 の元
の元  に作用させると,集合
に作用させると,集合 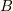 の元
の元  に変わる対応のことを言います.
この時,
に変わる対応のことを言います.
この時, 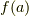 はただ一つの元に対応します.行き先が無いものや,複数の要素に変わるものがが一つでもあったら,それは写像ではなく,対応と言います.
はただ一つの元に対応します.行き先が無いものや,複数の要素に変わるものがが一つでもあったら,それは写像ではなく,対応と言います.
像  の定義は,
の定義は, 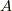 の部分集合
の部分集合 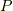 とし,
とし, 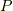 の全ての元
の全ての元  の写像先を集めてできた集合の事です.
引数が一つの元とは限らず,集合を取るところが写像と違います.
の写像先を集めてできた集合の事です.
引数が一つの元とは限らず,集合を取るところが写像と違います.
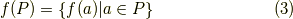
逆像 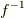 の定義は,
の定義は, 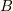 の部分集合
の部分集合 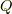 について,
について, 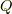 の中に行き先
の中に行き先  があるような
があるような 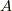 の中の元
の中の元  全ての集合です.
全ての集合です.
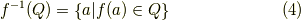
となります.
全射と単射
全射とは  の像が
の像が  に一致することを言います.つまり,写像の行き先
に一致することを言います.つまり,写像の行き先  のどの要素をとっても,写像元の
のどの要素をとっても,写像元の  が少なくとも1つは存在することになります.式で書くと
が少なくとも1つは存在することになります.式で書くと

となります.
単射とは任意の 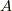 の異なる元
の異なる元  と
と 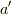 に対し,行き先が一致することは無いと言う事です.
に対し,行き先が一致することは無いと言う事です.
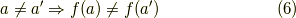
同じことを言いかえると,
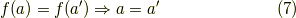
とも書けます.
式(1)と単射
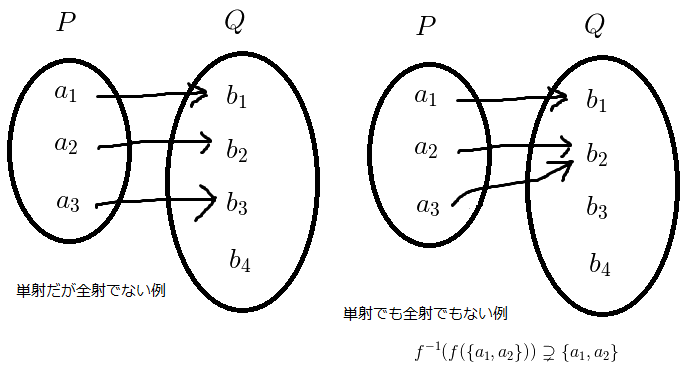
まず,式  を示しましょう.つまり,
を示しましょう.つまり,
theorem
を示します.
【大まかな流れ】
ここでは,  を見たす
を見たす  は必ず
は必ず  を満たすことを示します.
を満たすことを示します.
【証明】
まず,  を
を 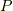 の任意の元とし
の任意の元とし 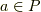 とします.すると,
とします.すると,  は写像なので唯一の行き先があり,
は写像なので唯一の行き先があり,  で,
で, 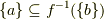 となるような
となるような 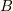 の元であり
の元であり 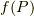 の元でもある
の元でもある  が存在します.
が存在します. 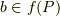 より,
より, 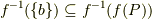 が成立します.よって,
が成立します.よって,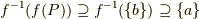 より,
より, 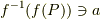 .つまり,
.つまり, 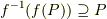 が言えました.■
が言えました.■
さて,これだけでは 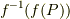 が
が 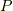 と同じ集合
と同じ集合  なのか,それとも
なのか,それとも 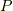 より真に小さい集合
より真に小さい集合 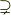 なのか区別がつきません.それを区別できるのが,
なのか区別がつきません.それを区別できるのが,  が単射かどうかなのです.
が単射かどうかなのです.
theorem
写像  が単射
が単射 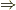
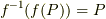
【証明】
「任意の 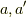 に対し
に対し 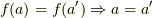 」ならば,
「任意の
」ならば,
「任意の  に対し
に対し 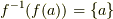 」となり,つまり,
」となり,つまり, 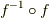 は恒等写像です.■
は恒等写像です.■
theorem
写像  が単射でない
が単射でない 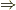
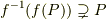
【証明の前に】
「単射である」は「任意の 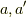 に対して
に対して  」でした.この否定は何でしょうか?ここで「
」でした.この否定は何でしょうか?ここで「 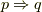 」とすると,下の表よりその否定は,
」とすると,下の表よりその否定は,
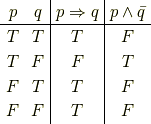
「 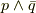 」つまり,
」つまり,
「ある 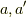 に対して
に対して 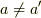 かつ
かつ  」です.
」です.
【証明】
「写像  が単射でない」
が単射でない」
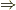
「ある 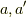 に対して
に対して 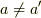 かつ
かつ  」
」
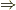
「 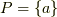 と置くと
と置くと 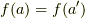 となる
となる 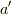 が存在し,
が存在し, 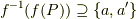 よって,
よって, 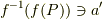 かつ
かつ 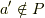 」
」
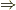
「 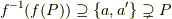 」
」
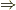
「  」■
」■
ここまでの話は「 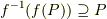 」と言う定理の下で,
」と言う定理の下で,
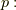 単射である
単射である

とすれば,
「 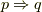 」かつ「
」かつ「 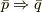 」が言えました.
これは「
」が言えました.
これは「  」と同値です.
」と同値です.
つまり,「  が単射であること」
が単射であること」 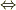 「
「 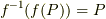 」
となり,右辺は集合が劣化しないと言い換えて良いでしょう.
これが単射の持つ性質です.
」
となり,右辺は集合が劣化しないと言い換えて良いでしょう.
これが単射の持つ性質です.
式(2)と全射
式 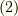 に対しても話は並行に進みます.
に対しても話は並行に進みます.
theorem
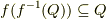
を示します.
【証明】
まず 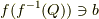 とすると,
とすると,  で,
で, 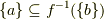 を満たす
を満たす 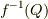 の元
の元  があります.
があります.  を作ると
を作ると 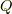 に入ります.すなわち,
に入ります.すなわち, 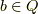 が言え,結論として,
が言え,結論として, 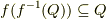 が言えました.■
が言えました.■
ここで,この定理には全射が関わってきます.見てみましょう.
theorem
写像  が(部分集合
が(部分集合 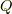 に対しての)全射である
に対しての)全射である 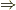
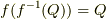
を示します.
【証明】
(部分集合 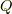 に対しての)と注が入りましたが,これは
に対しての)と注が入りましたが,これは 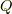 の中のどの元も写像元として
の中のどの元も写像元として 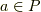 を持つことが保証されていると言う事です.まず
を持つことが保証されていると言う事です.まず 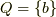 とし
とし 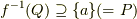 かつ
かつ 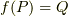 を満たす
を満たす  が少なくとも1つ存在します.
すると,
が少なくとも1つ存在します.
すると, 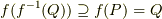 となります.ここで先ほど
となります.ここで先ほど 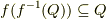 も言えましたから,晴れてめでたく
も言えましたから,晴れてめでたく 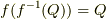 が言えました.■
が言えました.■
次に進みましょう.
theorem
写像  が(部分集合
が(部分集合 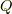 に対しての)全射でない
に対しての)全射でない 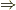

を示します.
【証明】
まず全射でないなら 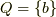 かつ
かつ  となる
となる  が存在します.すると,
が存在します.すると, 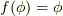 より,
より, 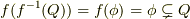 が言えます.今示すべきことは,「
が言えます.今示すべきことは,「 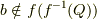 かつ
かつ 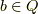 なる
なる  が存在すること」ですから,示せたことになります.■
が存在すること」ですから,示せたことになります.■
これらも,「  が(部分集合
が(部分集合 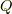 に対しての)全射であること」
に対しての)全射であること」 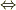 「
「 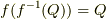 」が言えます.これも右辺は集合が劣化しないと言い換えて良いでしょう.これが全射の持つ性質です.
」が言えます.これも右辺は集合が劣化しないと言い換えて良いでしょう.これが全射の持つ性質です.
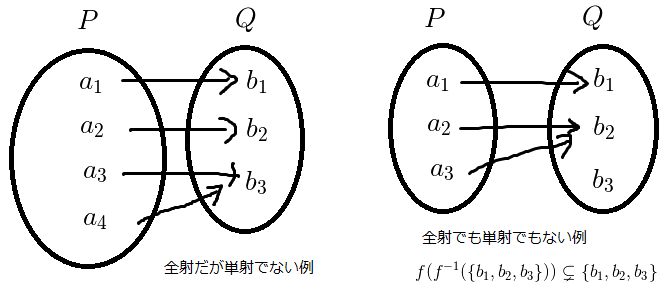
まとめ
直上の(部分集合 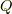 に対しての全射)と言う部分が気になりますが,「式
に対しての全射)と言う部分が気になりますが,「式 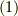 と単射」のセクションに対しても,(部分集合
と単射」のセクションに対しても,(部分集合 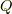 に対しての単射)と言う注を入れることができると分かります.つまり,下図で「
に対しての単射)と言う注を入れることができると分かります.つまり,下図で「 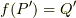 の範囲だけ見ると単射になっている(
の範囲だけ見ると単射になっている( 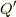 の外では単射になっていなくても良い)」と言う事です.
の外では単射になっていなくても良い)」と言う事です. 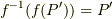 となるのが分かるのではないでしょうか.
となるのが分かるのではないでしょうか.
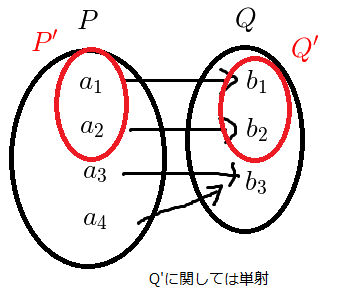
僕は最初,像と逆像の組み合わせがどんな時に恒等写像になって,そうでない時はどういう時かを調べてこの結論に達したのですが,とてもきれいな構造が見られて嬉しかったです.今日はここまで,お疲れさまでした!