この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
非弾性衝突の簡単なモデル
この記事では,完全弾性衝突 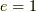 をする球同士の衝突でも,
非弾性衝突を起こしうる簡単な例を論じます.
をする球同士の衝突でも,
非弾性衝突を起こしうる簡単な例を論じます.
設定
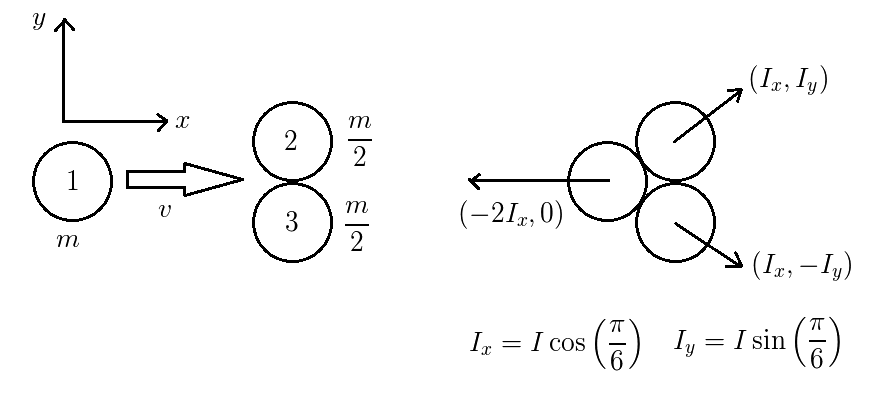
上図の様に完全弾性衝突を行う大きさの等しい球1,2,3を考え,それぞれの質量をm,m/2,m/2とします.
球1はx方向に速度vで運動しています.
球2と球3は自然長 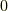 の減衰付きのばねでつながれて静止しているとします.
衝突の際はy軸に対して対称な衝突をし,
1と2の間で力積
の減衰付きのばねでつながれて静止しているとします.
衝突の際はy軸に対して対称な衝突をし,
1と2の間で力積 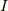 ,1と3との間で力積
,1と3との間で力積 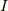 をそれぞれ交換します.
をそれぞれ交換します.
ここで注意することとして,反発係数の式は恐らくは使えません. よって,その代わり運動量保存則と運動エネルギー保存則を用いることを注意しておきます.
力積と運動量
今回は運動方程式ではなく,運動量と力積の関係を用います. 今回は瞬間的に力積を授受するのであって, もし運動方程式を用いるのでは互いに力を与えながら, 有限の距離を進まなければ,運動の変化が起こらないからです. 速度はIの関数として,次の様になります.
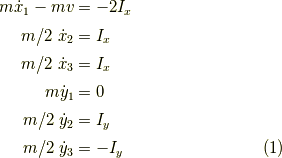
ここで,球の半径が等しいことで衝突の瞬間に正三角形ができますから,
球2,3が受ける力積の絶対値を 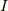 とすると,
とすると,
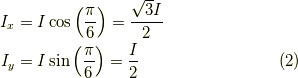
変数 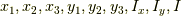 の9個に対し,
方程式が8つしかありません.条件がもう一つ必要です.
の9個に対し,
方程式が8つしかありません.条件がもう一つ必要です.
とりあえずは,速度を求めておきましょう.
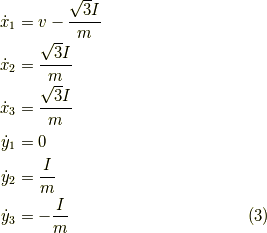
運動エネルギー保存の法則
さて,答えを言うと,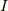 を決めるのに足りない条件は,
衝突直前,直後においての運動エネルギーの保存則から得られます.
を決めるのに足りない条件は,
衝突直前,直後においての運動エネルギーの保存則から得られます.
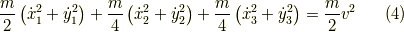
式 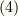 に式
に式 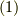 と
と 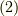 を代入すると,
を代入すると, 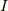 の二次式となります.
の二次式となります.
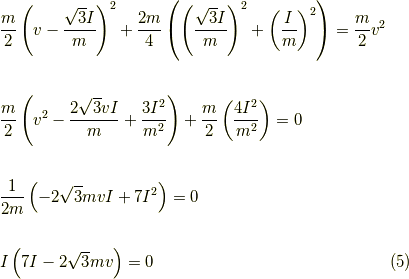
ここで 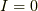 では素通りですので,
では素通りですので,

と決定されました.すると,式 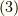 より,運動の全てが決定します.
より,運動の全てが決定します.
反発係数が1にならない
ここで興味があるのは,x軸方向の相対速度変化(反発係数)です.
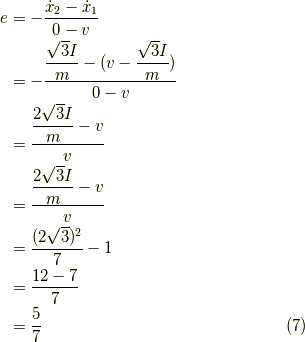
見事,反発係数は 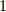 ではなくなりました.
私が思うに,今回はx方向の運動がy方向の運動自由度に逃げたのですが,
他の非弾性衝突も,このように何らかの他のエネルギー自由度に
散らばってしまうため,起こるのだと思います.
減衰付きばねは,得られたy方向の運動をやがて熱に変えます.
このばねは球2,3が飛び去ってしまうのを防ぐ為ですが,本質ではありません.
ではなくなりました.
私が思うに,今回はx方向の運動がy方向の運動自由度に逃げたのですが,
他の非弾性衝突も,このように何らかの他のエネルギー自由度に
散らばってしまうため,起こるのだと思います.
減衰付きばねは,得られたy方向の運動をやがて熱に変えます.
このばねは球2,3が飛び去ってしまうのを防ぐ為ですが,本質ではありません.
今日はここまで,お疲れ様でした.