この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。リンクを正しく張れていないところが存在しますのでご注意ください。正式公開まで、いましばらくお待ちください。
グリーン関数を理解しよう(ファインマンダイアグラム)

これからいくつかの記事を通して，物性物理で扱われる絶対零度におけるグリーン関数の理解を目指します．いくつかの定理などの証明は省略して，要点の俯瞰をする方針で行きます．参考文献として，下に書くMahan先生の本を挙げておきます．このシリーズでは 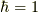$\hbar=1$ とします．前の記事はウィックの定理です．次の記事はダイソン方程式と自己エネルギーです．( 目次 )

基本的対応

この記事ではファインマンダイアグラムを学びます．まず，前回の最後の式を思い出しましょう．再掲すると，

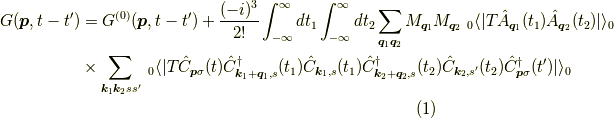
$G(\bm{p},t-t^\prime) &= G^{(0)}(\bm{p},t-t^\prime) + \dfrac{(-i)^3}{2!} \int_{-\infty}^\infty dt_1 \int_{-\infty}^\infty dt_2 \sum_{\bm{q}_1 \bm{q}_2} M_{\bm{q}_1} M_{\bm{q}_2} \ _0 \langle | T \hat{A}_{\bm{q}_1}(t_1) \hat{A}_{\bm{q}_2}(t_2) | \rangle_0 \\&\times \sum_{\bm{k}_1 \bm{k}_2 s s^\prime} \ _0 \langle | T \hat{C}_{\bm{p} \sigma}(t) \hat{C}^\dagger_{\bm{k}_1+\bm{q}_1, s}(t_1) \hat{C}_{\bm{k}_1,s}(t_1) \hat{C}^\dagger_{\bm{k}_2+\bm{q}_2, s}(t_2) \hat{C}_{\bm{k}_2,s^\prime}(t_2) \hat{C}^\dagger_{\bm{p} \sigma}(t^\prime) | \rangle_0\tag{1}$

という，相互作用のあるグリーン関数の自由なグリーン関数の展開の電子部分で，

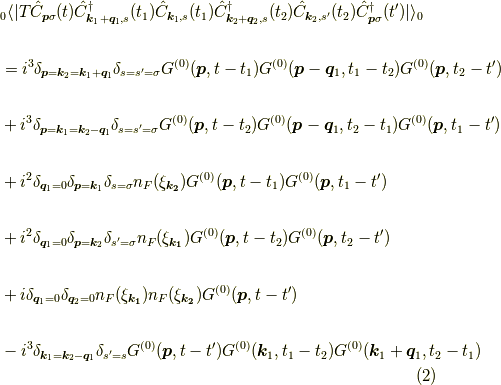
$&_0 \langle | T \hat{C}_{\bm{p} \sigma}(t) \hat{C}^\dagger_{\bm{k}_1+\bm{q}_1, s}(t_1) \hat{C}_{\bm{k}_1,s}(t_1) \hat{C}^\dagger_{\bm{k}_2+\bm{q}_2, s}(t_2) \hat{C}_{\bm{k}_2,s^\prime}(t_2) \hat{C}^\dagger_{\bm{p} \sigma}(t^\prime) | \rangle_0 \\ \\&= i^3 \delta_{\bm{p} = \bm{k}_2 = \bm{k}_1 + \bm{q}_1} \delta_{s=s^\prime=\sigma} G^{(0)}(\bm{p},t - t_1) G^{(0)}(\bm{p} - \bm{q}_1,t_1 - t_2) G^{(0)}(\bm{p},t_2 - t^\prime) \\ \\&+ i^3 \delta_{\bm{p} = \bm{k}_1 = \bm{k}_2 - \bm{q}_1} \delta_{s=s^\prime=\sigma} G^{(0)}(\bm{p},t - t_2) G^{(0)}(\bm{p} - \bm{q}_1,t_2 - t_1) G^{(0)}(\bm{p},t_1 - t^\prime) \\ \\&+ i^2 \delta_{\bm{q}_1 = 0} \delta_{\bm{p} = \bm{k}_1} \delta_{s=\sigma} n_F(\xi_{\bm{k_2}}) G^{(0)}(\bm{p},t - t_1) G^{(0)}(\bm{p},t_1 - t^\prime) \\ \\&+ i^2 \delta_{\bm{q}_1 = 0} \delta_{\bm{p} = \bm{k}_2} \delta_{s^\prime=\sigma} n_F(\xi_{\bm{k_1}}) G^{(0)}(\bm{p},t - t_2) G^{(0)}(\bm{p},t_2 - t^\prime) \\ \\&+ i \delta_{\bm{q}_1 = 0} \delta_{\bm{q}_2 = 0} n_F(\xi_{\bm{k_1}})n_F(\xi_{\bm{k_2}}) G^{(0)}(\bm{p},t - t^\prime) \\ \\&- i^3 \delta_{\bm{k}_1 = \bm{k}_2 - \bm{q}_1} \delta_{s^\prime = s} G^{(0)}(\bm{p},t-t^\prime) G^{(0)}(\bm{k}_1,t_1-t_2) G^{(0)}(\bm{k}_1 + \bm{q}_1,t_2-t_1)\tag{2}$

というものです．ここにさらにフォノンの自由グリーン関数がかかっています．

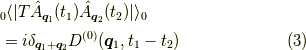
$&_0 \langle | T \hat{A}_{\bm{q}_1}(t_1) \hat{A}_{\bm{q}_2}(t_2) | \rangle_0 \\&= i \delta_{\bm{q}_1+\bm{q}_2} D^{(0)}(\bm{q}_1,t_1-t_2)\tag{3}$

今回はこの式 (2) をダイアグラムで表すことをします．それは，粒子の振る舞いを下図の様に対応させる手法です．

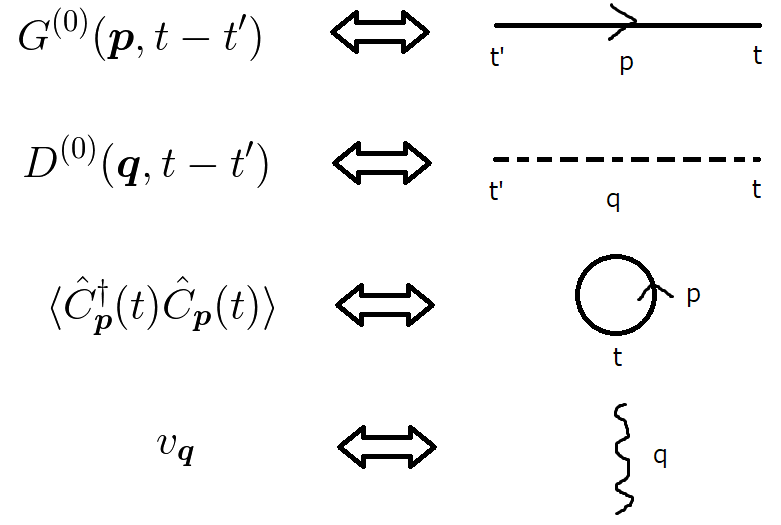
一番上の実線は自由な電子グリーン関数です．矢印が時間の流れ（左から右）へ付いているのは電子，逆行しているのは反粒子である陽電子です．

二番目の点線は自由なフォノングリーン関数です．この 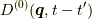$D^{(0)}(\bm{q},t-t^\prime)$ に矢印は付けません．というのは，，

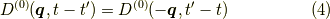
$D^{(0)}(\bm{q},t-t^\prime) = D^{(0)}(-\bm{q},t^\prime-t)\tag{4}$

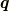と書けるので， $\bm{q}$ の符号は本質でないからです．

三番目は電子線のループです．同時刻の真空期待値 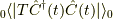$_0 \langle | T \hat{C}^\dagger(t) \hat{C}(t) | \rangle_0$ が粒子数演算子であることと関係があることが言えるはずですが，どうしてループと粒子数が関係するのか私は知りません．

最後はクーロン反発です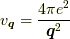． $v_{\bm{q}} = \dfrac{4 \pi e^2}{\bm{q}^2}$ のことですね．これはこの話においては同時刻に放出と吸収が起こるとしています．力が瞬間に伝わるという近似です．

なお，必ずしも 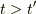$t>t^\prime$ ではありません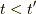． $t<t^\prime$ の時は時間を粒子が逆行する反粒子だと考えます．

個々のダイアグラム対応

以上を式 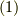(1) に対応させた図を載せていきます．

図1(a)．

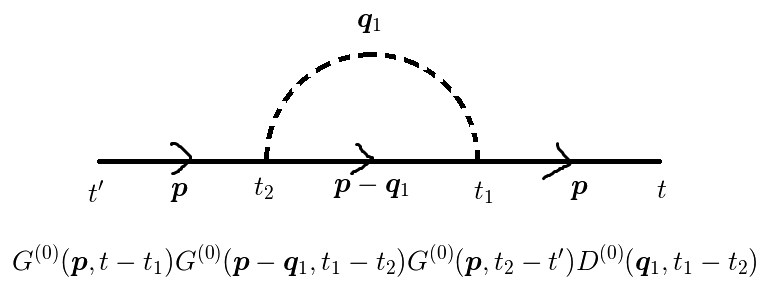
図1(b)

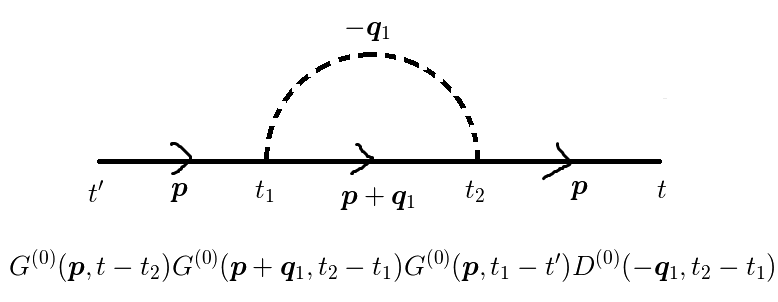
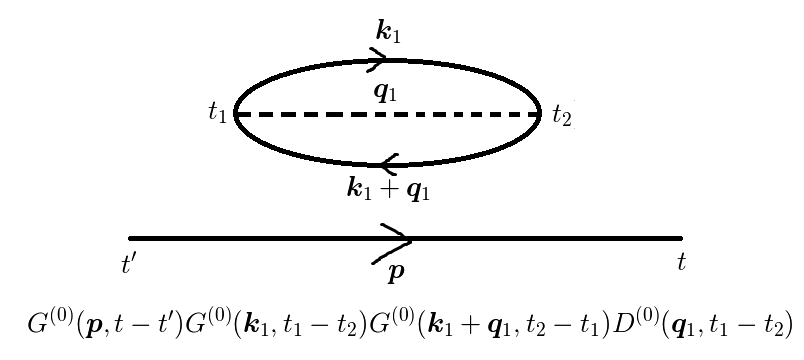
図1(c)

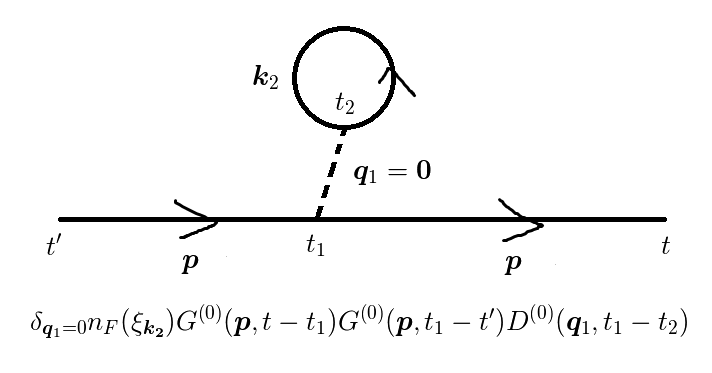
図1(d)

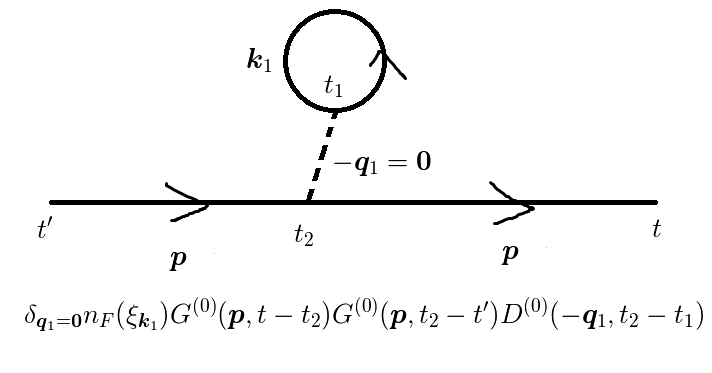
図1(e)

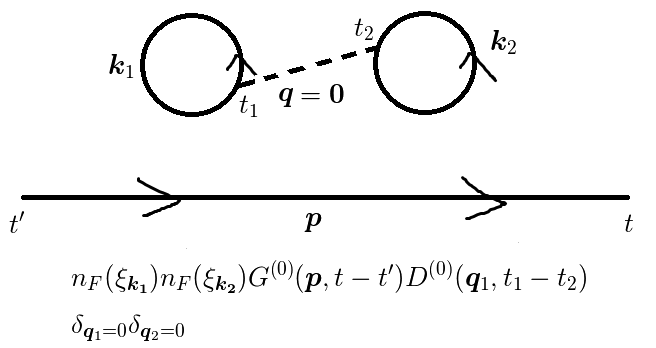
図1(f)

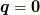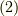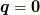さて，図(c),(d),(e)では波数ゼロのフォノンが出てきます．しかし， $\bm{q}=\bm{0}$ のフォノンは存在しません．よって，この項からの寄与はゼロと考えます．しいていえば，結晶の並進や恒久的なストレスのことですが，ハミルトニアンには関係しません．よって，前回の電子-フォノン相互作用の式 (2) の和からは， $\bm{q}=\bm{0}$ は除かれるべきだそうです．その和とは再掲しておくと，

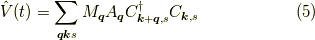
$\hat{V}(t) = \sum_{\bm{q}\bm{k}s} M_{\bm{q}} A_{\bm{q}} C^\dagger_{\bm{k}+\bm{q},s} C_{\bm{k},s}\tag{5}$

のことです．

図(a),(b)はまとめて考えると，

$\dfrac{1}{2!} &\int_{-\infty}^\infty dt_1 \int_{-\infty}^\infty dt_2 \sum_{\bm{q}} |M_{\bm{q}}|^2 D^{(0)}(\bm{q},t_1-t_2) \\&\times[G^{(0)}(\bm{p},t-t_1)G^{(0)}(\bm{p}-\bm{q},t_1-t_2)G^{(0)}(\bm{p},t_2-t^\prime) \\&+G^{(0)}(\bm{p},t-t_2)G^{(0)}(\bm{p}+\bm{q},t_2-t_1)G^{(0)}(\bm{p},t_1-t^\prime) ]\tag{6}$

今，この二つの項はパラメータ 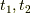t_1,t_2 の入れ替えで移り変わります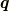． $\bm{q}$ の符号は

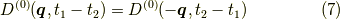
$D^{(0)}(\bm{q},t_1-t_2) = D^{(0)}(-\bm{q},t_2-t_1)\tag{7}$

を考えると，全く同じ寄与だと分かります．つまり，この前の因子 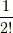$\dfrac{1}{2!}$ が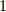に変わります．

図(f)は，

$G^{(0)}(\bm{p},t-t^\prime) F_1\tag{8}$

という寄与になります．ここで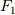， F_1 は

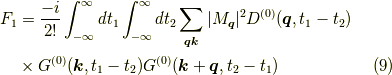
$F_1 &= \dfrac{-i}{2!} \int_{-\infty}^\infty dt_1 \int_{-\infty}^\infty dt_2 \sum_{\bm{q}\bm{k}} |M_{\bm{q}}|^2 D^{(0)}(\bm{q},t_1-t_2) \\&\times G^{(0)}(\bm{k},t_1-t_2) G^{(0)}(\bm{k}+\bm{q},t_2-t_1)\tag{9}$

という（無限大の）定数因子です．

真空偏極項とキャンセル定理

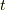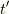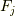この図(f)の様につながっていないグラフを非連結グラフと言います．そして，か $t^\prime$ とつながっている電子線が外線といいます．その閉じたループで外線とつながっていない部分をバブルと言います．もっと高次の非連結グラフ F_j もあります．それらもやはり定数を掛け算する寄与になります．それらをトータルしたものを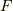とします．ゼロ次の自由なグリーン関数そのものの寄与 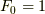F_0 = 1 として，

$F = \sum_{j=0}^\infty F_j\tag{10}$

となります．ここでウィックの定理を思い出しましょう．

相互作用のあるグリーン関数とその分母 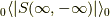$_0\langle |S(\infty,-\infty)| \rangle_0$ を比較してみます．

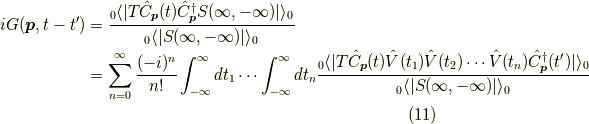
$i G(\bm{p},t-t^\prime) &= \dfrac{_0 \langle | T \hat{C}_{\bm{p}}(t) \hat{C}^\dagger_{\bm{p}} S(\infty,-\infty) | \rangle_0}{_0 \langle | S(\infty,-\infty) | \rangle_0} \\&= \sum_{n=0}^\infty \dfrac{(-i)^{n}}{n!} \int_{-\infty}^\infty dt_1 \cdots \int_{-\infty}^\infty dt_n \dfrac{_0 \langle | T \hat{C}_{\bm{p}}(t) \hat{V}(t_1) \hat{V}(t_2) \cdots \hat{V}(t_n) \hat{C}^\dagger_{\bm{p}}(t^\prime) | \rangle_0}{_0 \langle | S(\infty,-\infty) | \rangle_0}\tag{11}$

と，

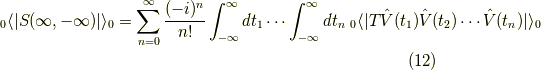
$_0 \langle |S(\infty,-\infty) | \rangle_0 &= \sum_{n=0}^\infty \dfrac{(-i)^{n}}{n!} \int_{-\infty}^\infty dt_1 \cdots \int_{-\infty}^\infty dt_n \ _0 \langle | T \hat{V}(t_1) \hat{V}(t_2) \cdots \hat{V}(t_n) | \rangle_0\tag{12}$

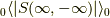です．この $_0 \langle |S(\infty,-\infty) | \rangle_0$ の内容を考えると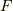に等しいことが分かります．外線の無い（足の無い）相互作用のあるグリーン関数と言えば分かるでしょうか．よくよく考えてみると，グリーン関数の内で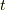を含むものと 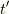$t^\prime$ を含むものは必ずつながっています．なぜなら，電子線に分岐や行き止まりはないからです．すると，残りの部分はバブルになっていると分かります．相互作用のあるグリーン関数 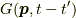$G(\bm{p},t-t^\prime)$ の内で，バブルが無く，かつ，ありうる全てのつながり方を持っている関数を考え，これを連結グリーン関数 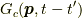$G_c(\bm{p},t-t^\prime)$ とします．またここで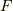，は全てのバブルの寄与でした．

図2

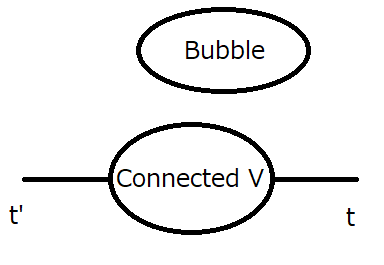
すると，これは図2を見ると，

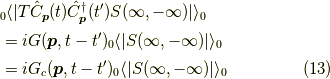
$&_0 \langle | T \hat{C}_{\bm{p}}(t) \hat{C}^\dagger_{\bm{p}}(t^\prime) S(\infty,-\infty) | \rangle_0 \\&=iG(\bm{p},t-t^\prime) _0 \langle | S(\infty,-\infty) | \rangle_0 \\&=iG_c(\bm{p},t-t^\prime) _0 \langle | S(\infty,-\infty) | \rangle_0\tag{13}$

つまり，

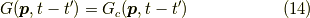
$G(\bm{p},t-t^\prime) = G_c(\bm{p},t-t^\prime) \tag{14}$

がいえることになります．はて，何が嬉しいの？と仰る方もいるかもしれません．いえいえ，これは凄いことです．同じ結果を得るのに，連結なものだけを考えることで良い．と言う事になったからです．こうして，相互作用のあるグリーン関数 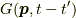$G(\bm{p},t-t^\prime)$ の計算は大幅に簡略化されたことになります．

トポロジー的分類

先ほど図(a),(b)は等しい事が言えましたね．同様に次の連結な摂動はパラメータの置き換えが通りあります．

つまり，

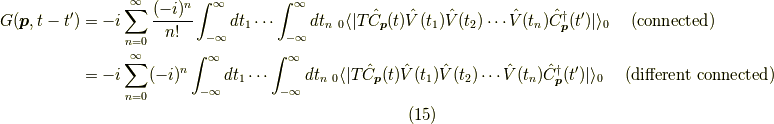
$G(\bm{p},t-t^\prime) &= -i \sum_{n=0}^\infty \dfrac{(-i)^{n}}{n!} \int_{-\infty}^\infty dt_1 \cdots \int_{-\infty}^\infty dt_n \ _0 \langle | T \hat{C}_{\bm{p}}(t) \hat{V}(t_1) \hat{V}(t_2) \cdots \hat{V}(t_n) \hat{C}^\dagger_{\bm{p}}(t^\prime) | \rangle_0 \ \ \ \ (\rm{connected}) \\&= -i \sum_{n=0}^\infty (-i)^{n} \int_{-\infty}^\infty dt_1 \cdots \int_{-\infty}^\infty dt_n \ _0 \langle | T \hat{C}_{\bm{p}}(t) \hat{V}(t_1) \hat{V}(t_2) \cdots \hat{V}(t_n) \hat{C}^\dagger_{\bm{p}}(t^\prime) | \rangle_0 \ \ \ \ (\rm{different \ connected}) \tag{15}$

これもまた計算の手間を簡略化してくれることです．

今日はここまで，お疲れ様でした．

次の記事はダイソン方程式と自己エネルギーです．

参考文献

Gerald D.Mahan著，『 Many-Particle Physics Third Edition (Physics of Solids and Liquids)』（ Springer， 2010， Chap2）

[home] [量子力学] [ページの先頭]