この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
フェルミ面とは
これを読めばフェルミ面がなぜ単純な球とならないかが分かると思います.まず,一次元の議論を手短にして,その後,二次元の議論をします.
ブロッホの定理
ブロッホの定理の要点は,周期 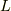 のポテンシャルの波動関数
のポテンシャルの波動関数 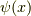 は,周期
は,周期 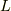 の関数
の関数 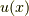 を用いて,
を用いて,
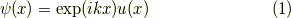
- と書けるという事です.大体
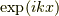 の周期は
の周期は 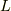 よりもずっと大きいです.
よりもずっと大きいです.
クローニッヒペニーポテンシャル
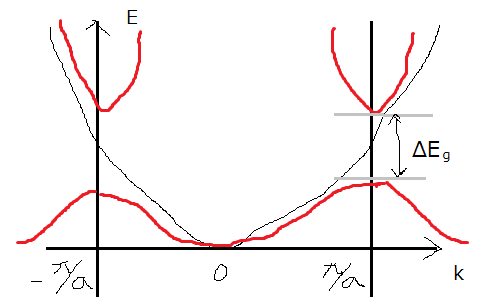
クローニッヒペニーポテンシャルの議論の要点を書きます.周期的なポテンシャルをもつ一次元結晶のブロッホ波 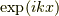 のkとエネルギーEの関係は,自由な電子の放物線型の関係と違い,下図の様に結晶の第一ブリルアンゾーンの端でエネルギー順位が反発を起こし,エネルギーギャップが空くと言うものです.この赤線の書き方を「周期的ゾーン形式」と言います.一般にエネルギー量子数が異なる軌道同士はこの様に反発し,エネルギーギャップが空きます.
のkとエネルギーEの関係は,自由な電子の放物線型の関係と違い,下図の様に結晶の第一ブリルアンゾーンの端でエネルギー順位が反発を起こし,エネルギーギャップが空くと言うものです.この赤線の書き方を「周期的ゾーン形式」と言います.一般にエネルギー量子数が異なる軌道同士はこの様に反発し,エネルギーギャップが空きます.
図1
二次元格子のフェルミ面
さて,ここからが本題です.正方形の格子を考えます.すると,自由電子のエネルギーのグラフは次のような放物面になります.

ここで原点を通るx軸に平行な  軸をもつ断面で,グラフを書くと,やはり反発が起き,先ほどの図の様になります.では,これを
軸をもつ断面で,グラフを書くと,やはり反発が起き,先ほどの図の様になります.では,これを  方向にずらした断面を取るとどうなるでしょう.それは,式(2)より先ほどの図を上方向に平行移動したグラフに大体なります.大体と言ったのは,軌道の反発の形がおそらくは厳密には異なるからです.
方向にずらした断面を取るとどうなるでしょう.それは,式(2)より先ほどの図を上方向に平行移動したグラフに大体なります.大体と言ったのは,軌道の反発の形がおそらくは厳密には異なるからです.
フェルミ面とはなんだったでしょう?それは,軌道の下の順位からパウリの排他律に従い,電子を詰めていったときの,一番上のエネルギーでした.これは全てのグラフにおいて同一の高さになります.よって,
図2
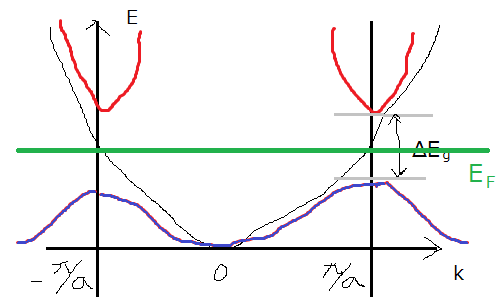
図3
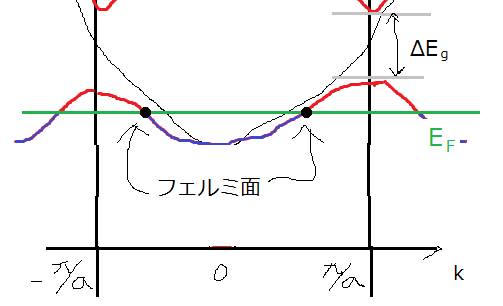
図2と3の様に原点から離れた断面ほどフェルミ面は小さくなります.図2では,フェルミ面は隣のブリルアンゾーンとくっついています.よって,フェルミ面を正方形上に描くと,図4の様に境界がくっついた歪んだ円となります.
図4
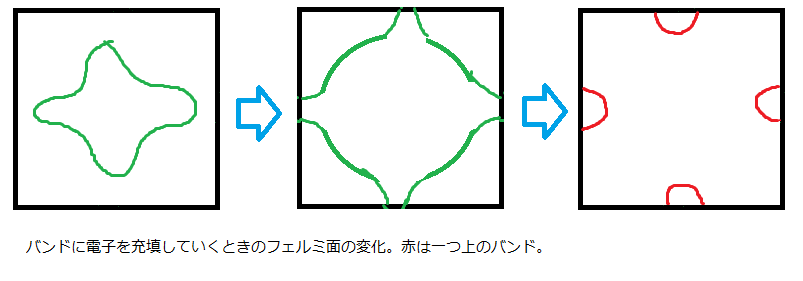
注意したいのは,軌道は電子が有る無いにかかわらず,自由電子のそれである放物面から反発・変形して存在し,そこに一原子あたり1ないし,2,3個等の電子が詰まっていくのです.
思うに,この様に逆格子空間と言うのは,本来なら結晶全体に波として存在している電子の波動関数をフェルミ面として見る事が出来る,まさにそれが固体物理学で逆格子空間を学ぶ意義なんだと思います.
今日はここまで.お疲れ様でした.