この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。リンクを正しく張れていないところが存在しますのでご注意ください。正式公開まで、いましばらくお待ちください。
ホロノーム型の拘束条件

ここでは，解析力学の問題を解くときに重要となってくる拘束条件の処理を機械的に行ってしまう方法(ラグランジュの未定乗数法)を紹介します．ただ，その証明にはいくつかの補題が必要となりますから，この記事では割愛して，技術の習得だけを目的にしたいと思います．

ホロノーム型の拘束条件

力学の問題を使って拘束条件の例を挙げて見ましょう．例えば質量の物体がある道に沿って運動するというのも拘束条件の一つですし，大きさのある物体を剛体で近似することも原子や分子間の相対距離を固定する拘束条件の一種だと考えることができます．

このように，拘束条件は具体的な問題を解く上で避けることはできない関門です．しかし，先ほど挙げた例はいずれも物体の軌跡や粒子間の相対的な位置関係を固定するもので，座標に関する拘束条件でした．多くの場合は拘束条件を一般座標 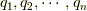$q_1,q_2,\cdots,q_n$ と時間の関数を複数用いて次のように表すことができるでしょう．

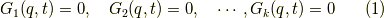
$G_1(q,t)=0,\quad G_2(q,t)=0,\quad\cdots, G_k(q,t)=0 \tag{1}$

例えば，平面内を物体が放物運動するように壁を作って物体を転がしたというような場合は 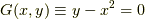$G(x,y)\equiv y-x^2=0$ などというように表すことができます．式(1)のように書ける拘束条件をホロノーム型の拘束条件と言います．

では，式(1)の形ですべての拘束条件を網羅できるかというと，そうではありません．式(1)のように表すことのできないものも存在して，そのような拘束条件を総称して非ホロノーム型の拘束条件と呼びます．

ここでは，ホロノーム型の拘束条件の処理を考えましょう．なんとホロノーム型の拘束条件はラグランジュの未定乗数法を使うと統一的に扱うことができてしまうのです！

ラグランジュの未定乗数法

一般にホロノーム型の拘束条件が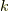個あれば，自由度は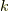だけ減って n-k になります(つまり，独立に動かせる変数が n-k 個になるということです)．

ここで，式(1)で表せる拘束条件を考えてみましょう．この系のラグランジアンをと書くことにすると，今までどおり作用を

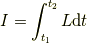
$I=\int_{t_1}^{t_2}L\mathrm{d}t$

と定義できます．この第一変分をとると，これまでと全く同様に計算できて，次のようになります．

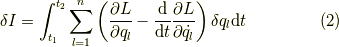
$\delta I=\int_{t_1}^{t_2}\sum_{l=1}^{n}\left({\partial L\over \partial q_l}-{\mathrm{d}\over\mathrm{d}t}{\partial L\over \partial \dot{q}_l}\right)\delta q_l\mathrm{d}t \tag{2}$

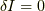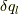さて，ここで困ることになります．確かに変分原理より $\delta I=0$ を要請することになりますが，拘束条件(1)のために各変分 $\delta q_l$ を独立にとることができません！

このままではどうしようもないので，拘束条件をうまく使っていきましょう．まず，拘束条件について変分をとります．式で表すと次のようになるでしょう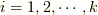． $i=1,2,\cdots,k$ とします．

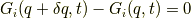
$G_i(q+\delta q,t)-G_i(q,t)=0$

これを，変分について一次の項までとることにしましょう．

$\sum_{l=1}^{n}{\partial G_i\over\partial q_l}\delta q_l=0 \tag{3}$

これで，拘束条件と変分の関係を見ることができるようになりました．ここで，ラグランジュの未定乗数法と呼ばれるものを使うことになります．

アイディアは簡単です．今考えている座標変数のうち独立なものが n-k 個しかなくて困っているわけですから，新しく値が未定の定数を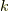個用意して，とにかく新しい定数にに制限を押し付けてしまえば座標変数はすべて独立に取れてしまうのではないか？ということです．

具体的には次のようにします．新しい定数 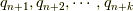$q_{n+1},q_{n+2},\cdots,q_{n+k}$ を導入します．これはラグランジュの未定乗数と呼ばれています．式(2)と式(3)から次の式が成り立つでしょう．

$\int_{t_1}^{t_2}\sum_{l=1}^{n}\left({\partial L\over \partial q_l}-{\mathrm{d}\over\mathrm{d}t}{\partial L\over \partial \dot{q}_l}+\sum_{i=1}^{k}q_{n+i}{\partial G_i\over\partial q_l}\right)\delta q_l\mathrm{d}t=0 \tag{4}$

さて，未定乗数をうまく選べば変分がすべて独立に取れるようになりますから，次の等式が成り立ちます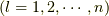． $(l=1,2,\cdots,n)$

${\mathrm{d}\over\mathrm{d}t}{\partial L\over \partial \dot{q}_l}-{\partial L\over \partial q_l}-\sum_{i=1}^{k}q_{n+i}{\partial G_i\over\partial q_l}=0 \tag{5}$

あとは，式(1)で表される拘束条件の式とあわせて解けば，良いことになります．これでラグランジュの未定乗数法は完成です．

式(1)と式(5)をまとめて書くこともできます．新しくラグランジアン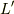を次の式で定義します．

$L'(q,\dot{q},t;q_{n+1},q_{n+2},\cdots,q_{n+k})=L(q,\dot{q},t)+\sum_{i=1}^{k}q_{n+i}G_i(q,t)$

新しいラグランジアン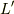について，いつも通りのラグランジュの運動方程式を使うと式(1)と式(5)が全部表せてしまうことを確認してください．

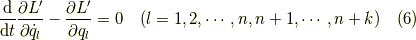
${\mathrm{d}\over\mathrm{d}t}{\partial L'\over \partial \dot{q}_l}-{\partial L'\over \partial q_l}=0 \quad (l=1,2,\cdots,n,n+1,\cdots,n+k) \tag{6}$

つまり，ホロノーム型の拘束条件はラグランジアンに取り込んでしまうことができるのです．この性質は，拘束条件がないとして議論したことはホロノーム型の拘束条件が課されたときも成り立つということを意味しますので，非常に便利ですね．

[home] [解析力学] [ページの先頭]