この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
留数定理の積分路が原点を囲む囲まないかの違いについて
この記事では,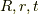 を実数とした時,
を実数とした時, 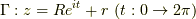 とした時の
とした時の 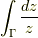 を考えます.工学的な記述であって,あまり数学的厳密性はありません.
を考えます.工学的な記述であって,あまり数学的厳密性はありません.
計算の実行
上に述べたとおりの条件で,積分を行います. 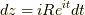 より,
より,
![\int_\Gamma \dfrac{dz}{z} &= \int_{t=0}^{2 \pi} \dfrac{iRe^{it}}{Re^{it} + r} dt \\&= \left[ \rm{log}|Re^{it} + r| \right]_{t=0}^{2 \pi} \\&= \left[ \rm{Log}|Re^{it} + r| + i \phi \right]_{t=0}^{2 \pi} \tag{1}](http://hooktail.maxwell.jp/kagi/0d421d2906a4b53f5da049dd9f70ddda.png)
ここで,実部は 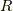 と
と  の値に関わらず,
の値に関わらず,
![\left[ \rm{Log}|Re^{it} + r| \right]_{t=0}^{2 \pi} = 0 \tag{2}](http://hooktail.maxwell.jp/kagi/172006836905a33518dd9d92a0ddffab.png)
です. 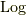 は引数に実数を取り普通の実関数の
は引数に実数を取り普通の実関数の 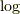 と同じ値を返します.
これを「対数の主値」と言います.一方,
と同じ値を返します.
これを「対数の主値」と言います.一方, 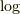 の虚部
の虚部 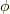 は,
は,
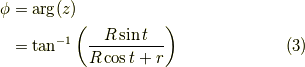
となります.
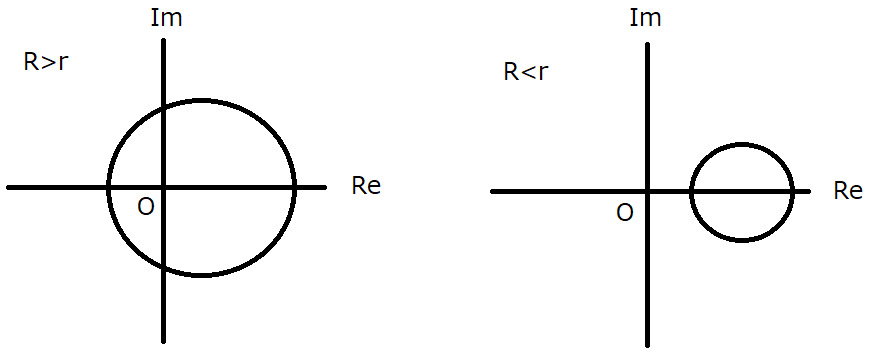
R<rの時
これは,原点から見て 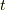 が
が 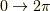 まで動くとき,
まで動くとき, 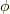 は
は 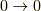 を動きます.
積分路が原点を囲わない為,
を動きます.
積分路が原点を囲わない為, 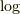 のリーマン面の分枝を跨がない為です.
のリーマン面の分枝を跨がない為です.
よって,

となります.
R>rの時
この時は,注意が必要です.
なぜならば, 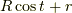 がゼロになる
がゼロになる 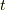 が二つあるからです.これに対応する
が二つあるからです.これに対応する 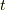 を
を 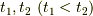 とします.ここで小さな正の実数
とします.ここで小さな正の実数 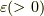 を用意します.
を用意します. 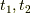 を除いて
を除いて 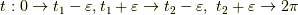 とすればよいようです.この時,
とすればよいようです.この時, 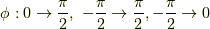 と動きますから,その後で
と動きますから,その後で 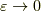 とすればよく,
とすればよく,
![&\left[ i \phi \right]_{t=0}^{t_1 - \varepsilon} + \left[ i \phi \right]_{t=t_1 + \varepsilon}^{t_2 - \varepsilon} + \left[ i \phi \right]_{t=t_2 + \varepsilon}^{2 \pi} \\&\to i(\dfrac{\pi}{2}-0)+i(\dfrac{\pi}{2}-(-\dfrac{\pi}{2}))+i(0-(-\dfrac{\pi}{2})) \\&= 2 \pi i \tag{5}](http://hooktail.maxwell.jp/kagi/f2e31b66d65ca97a7e54055f3e770290.png)
となります.
R=rの時
この場合は,
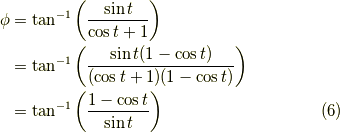
となります.ここで 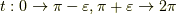 の時,
の時, 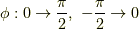 となるので,
となるので,
![&\left[ i \phi \right]_{t=0}^{\pi - \varepsilon} + \left[ i \phi \right]_{t=\pi + \varepsilon}^{2 \pi} \\&\to i(\dfrac{\pi}{2}-0)+i(0-(-\dfrac{\pi}{2})) \\&= \pi i \tag{7}](http://hooktail.maxwell.jp/kagi/ef790a4d4cc6dba6aa14e40b20ade09c.png)
となります.
まとめ
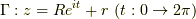 の時,
の時,
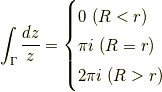
となります.
今日はここまで,お疲れさまでした.