この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
統計力学におけるシャノンのエントロピーの導出
この記事では,シャノンのエントロピー 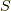 ,つまり,
,つまり,
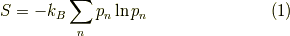
をカノニカル集団(正準集団)の基礎から導出します.
β<E>の書き換え
これはよく知られている公式を用います.つまり,
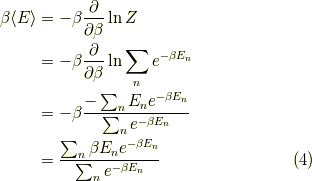
βFの書き換え
統計力学的定義に戻りますと,ヘルムホルツの自由エネルギー 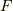 は,
は,
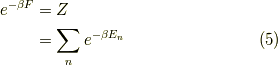
もしくは,

です.ここで,次のボルツマン分布を確認しておきます.
縮退していてもよい,つまり, 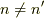 でも,
でも, 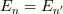 であってよいのです.
エネルギー準位
であってよいのです.
エネルギー準位 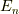 をとる確率
をとる確率 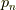 は,
マクスウェル・ボルツマン分布により,
は,
マクスウェル・ボルツマン分布により,
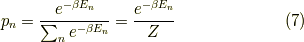
書き換えると,

となります.
式 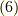 より,
より,
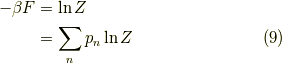
と書いておきます.ここで, 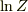 は
は 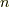 の依存性がないので,式
の依存性がないので,式 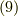 の様に書けるのがポイントです.
なぜなら,
の様に書けるのがポイントです.
なぜなら,

であるからです.
いよいよ導出
式 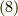 ,式
,式  より,
より,
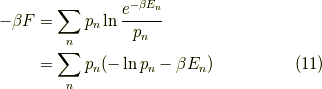
ですね?
少し戻って,式  を書き直すと,
を書き直すと,
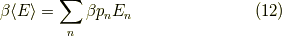
ですから,式 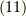 と式
と式 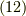 より,
より,
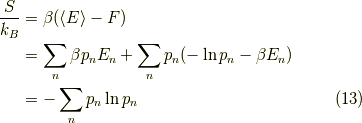
つまり,
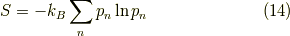
が導けました.
こうしてシャノンエントロピーが導けました.
最初にこれを考えた,ボルツマンやギブスはとてもすごいと思います.
それでは,今日はこの辺で,お疲れさまでした.
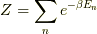 からエネルギー期待値
からエネルギー期待値 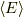 と ヘルムホルツの自由エネルギー
と ヘルムホルツの自由エネルギー 
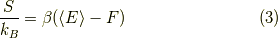
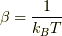 です.
です.