この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
リー微分の導出方法(ベクトルと1形式)
最近,リー微分を勉強していたのですが, ベクトルと一形式の両方を素直な方法で求めている本が無かったので自分で求めてみました. 下に挙げる参考文献 理論物理学のための幾何学とトポロジーI を読みながら, この記事を読むといいと思います.
ベクトルのリー微分
ベクトルのリー微分の定義は,
![\mathcal{L}_X Y = \lim_{\varepsilon \to 0} \dfrac{1}{\varepsilon} \left[ (\sigma_{-\varepsilon})_* Y|_{\sigma_{\varepsilon(x)}} - Y|_x \right] \tag{1}](http://hooktail.maxwell.jp/kagi/562fdd865b8243b7789a20e7debbaf7e.png)
です.
直感的なイメージは,曲面上に滑らかなベクトル場 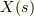 (
(  は位置を表すパラメータ)があって,それをある点
は位置を表すパラメータ)があって,それをある点 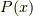 において(
において(  は座標),別のベクトル場について,その点で
は座標),別のベクトル場について,その点で 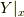 だったとします.
ここで
だったとします.
ここで 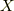 に沿って微小量
に沿って微小量 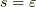 だけ進める操作を
だけ進める操作を 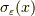 で表し,すると,
で表し,すると, 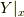 は
は  となります.
ここで,両者の微分を考えるわけです.しかし,ベクトル
となります.
ここで,両者の微分を考えるわけです.しかし,ベクトル 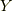 自体が変化するのはもちろん,この二つのベクトルは別の点から出ているので,基底ベクトル
自体が変化するのはもちろん,この二つのベクトルは別の点から出ているので,基底ベクトル 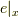 と
と 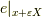 が同じではありません.
よって,その補正を
が同じではありません.
よって,その補正を 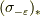 で行う訳です.下についた
で行う訳です.下についた  は,微分写像と言うもので,表示の方法を変えるというイメージを持つといいと思います.
これは簡単に言うと,
は,微分写像と言うもので,表示の方法を変えるというイメージを持つといいと思います.
これは簡単に言うと, 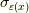 のベクトルを"平行移動"して,
のベクトルを"平行移動"して,  まで運んだ場合に換算したものです.その間,曲がった空間では微妙に基底ベクトル
まで運んだ場合に換算したものです.その間,曲がった空間では微妙に基底ベクトル  は変化します.
それを踏まえて,式
は変化します.
それを踏まえて,式 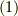 を計算します.
を計算します.
![Y|_{\sigma_\varepsilon(x)} &= Y^\mu (x^\nu + \varepsilon X^\nu ) e_\mu|_{x + \varepsilon X} \\&\simeq \left[ Y^\mu + \varepsilon X^\nu (\partial_\nu Y^\mu ) \right] e|_{x + \varepsilon X} \tag{2}](http://hooktail.maxwell.jp/kagi/7accf503d8f03011d7fa075e3814592a.png)
ここで 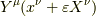 のカッコは引数であって積ではないです.
また
のカッコは引数であって積ではないです.
また 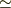 を使いましたが,以降では
を使いましたが,以降では  の二次以上の項を無視してイコールで結ぶことにします.
では,基底ベクトルを変換しましょう.先にある(
の二次以上の項を無視してイコールで結ぶことにします.
では,基底ベクトルを変換しましょう.先にある(  の大きい)基底ベクトルを戻してくる(
の大きい)基底ベクトルを戻してくる(  を小さい方へ動かす)ので
を小さい方へ動かす)ので 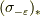 の添え字は,
の添え字は,  ではなく
ではなく 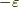 となります.
となります.

式 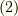 と
と 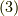 を合わせて,リー微分を求めましょう.
を合わせて,リー微分を求めましょう.
![(\sigma_{-\varepsilon})_* Y|_{\sigma_\varepsilon(x)} &= Y^\mu (x^\nu + \varepsilon X^\nu ) (\sigma_{-\varepsilon})_* e_\mu|_{x + \varepsilon X} \\&= \left[ Y^\mu + \varepsilon X^\nu (\partial_\nu Y^\mu) \right] \left[ \partial_\mu \left( x^\nu - \varepsilon X^\nu \right) \right]e_\nu|_x \\&= \left[ Y^\mu + \varepsilon X^\lambda (\partial_\lambda Y^\mu) \right] \left[ \delta_\mu^\nu - \varepsilon (\partial_\mu X^\nu) \right]e_\nu|_x \\&= Y^\mu e_\mu|_x + \varepsilon \left[ X^\lambda (\partial_\lambda Y^\mu) e_\mu|_x - Y^\mu (\partial_\mu X^\nu) e_\nu|_x \right] \\&= Y^\mu e_\mu|_x + \varepsilon \left[ X^\mu (\partial_\mu Y^\nu) - Y^\mu (\partial_\mu X^\nu) \right] e_\nu|_x \tag{4}](http://hooktail.maxwell.jp/kagi/7382d1684069517e3b6ccdb46be66a13.png)
ですから,
![\mathcal{L}_X Y = \left[ X^\mu (\partial_\mu Y^\nu) - Y^\mu (\partial_\mu X^\nu) \right] e_\nu|_x \tag{5}](http://hooktail.maxwell.jp/kagi/519bd6a16861b0dfdb289ca40c21062d.png)
となります.ちなみに 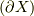 は偏微分がカッコの外には及ばないことを意味しています.ご注意を.
は偏微分がカッコの外には及ばないことを意味しています.ご注意を.
1形式のリー微分
自分が調べた限りでは,多くの文献では内部積と言う概念を用いて,1形式のリー微分を定義しています. 2形式,3形式などへの拡張が容易だからです.参考文献では幾何学的イメージを大切にした導出法が書いてあるのですが,ベクトルについてだけしか書かれていません.一形式についても残しておくべきだと思うので,ここに書きます.
1形式のリー微分の定義は,
![\mathcal{L}_X \omega = \lim_{\varepsilon \to 0} \dfrac{1}{\varepsilon}\left[ (\sigma_\varepsilon)^* \omega|_{\sigma_\varepsilon(x)} - \omega|_x \right] \tag{6}](http://hooktail.maxwell.jp/kagi/cd6fe073360b5d20676168d63570bbdb.png)
です.
引き戻しと言う概念を必要とします.
今回使う形は, 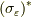 です.微分写像と引き戻しは対になる概念です.
微分写像はベクトルに作用します.一方,引き戻しは1形式に作用します.
"引き戻しの定義"は,
です.微分写像と引き戻しは対になる概念です.
微分写像はベクトルに作用します.一方,引き戻しは1形式に作用します.
"引き戻しの定義"は,
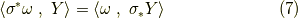
を満たす演算です.ここで, 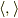 は内積です.
内積は対応する(同一点から伸びる)双対空間のペアで行われるということです.今必要なのは,基底ベクトル同士の関係ですから,
は内積です.
内積は対応する(同一点から伸びる)双対空間のペアで行われるということです.今必要なのは,基底ベクトル同士の関係ですから, 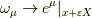 ,
, 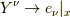 を代入します.すると,式
を代入します.すると,式 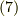 の右辺は,
の右辺は,
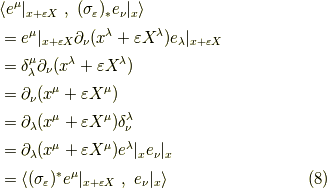
と,式 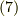 の左辺にたどり着けることが分かります.ここで,
の左辺にたどり着けることが分かります.ここで, 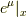 と
と 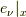 は双対ベクトルであることを使いました.つまり,
は双対ベクトルであることを使いました.つまり, 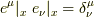 です.最後の
です.最後の 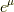 の位置が
の位置が  ではなく
ではなく 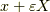 なのはそれが定義だからです.よって,
なのはそれが定義だからです.よって,
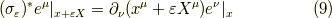
が言えました.リー微分は次の計算から求まります.
![(\sigma_{\varepsilon})^* \omega|_{\sigma_\varepsilon(x)} &= \omega_\mu|_{\sigma_\varepsilon(x)} (\sigma_{\varepsilon})^* e^\mu|_{x + \varepsilon X} \\&= \left[ \omega_\mu + \varepsilon X^\lambda(\partial_\lambda \omega_\mu) \right] \left[ \partial_\nu (x^\mu + \varepsilon X^\mu) \right] e^\nu|_x \\&= \left[ \omega_\mu + \varepsilon X^\lambda(\partial_\lambda \omega_\mu) \right] \left[ \delta_\nu^\mu + \varepsilon (\partial_\nu X^\mu)) \right] e^\nu|_x \\&= \omega_\mu \delta_\nu^\mu e^\nu|_x + \varepsilon X^\lambda(\partial_\lambda \omega_\mu) \delta_\nu^\mu e^\nu|_x + \varepsilon \omega_\mu (\partial_\nu X^\mu) e^\nu|_x \\&= \omega_\mu e^\mu|_x + \varepsilon \left[ X^\nu(\partial_\nu \omega_\mu) + \omega_\nu (\partial_\mu X^\nu) \right] e^\mu|_x \tag{10}](http://hooktail.maxwell.jp/kagi/82fba55b78c876c672feea788455e99f.png)
となることから,
![\mathcal{L}_X \omega = \left[ X^\nu(\partial_\nu \omega_\mu) + \omega_\nu (\partial_\mu X^\nu) \right] e^\mu|_x \tag{11}](http://hooktail.maxwell.jp/kagi/4537dc2318a9b87a64c2a7be46e527eb.png)
となります.
おまけ
ここで使った,ベクトルの変換について,少し補足を書いておきます.
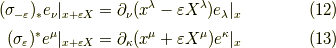
でした.行列として考えるなら, 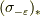 と
と  は逆行列です.
実際,
は逆行列です.
実際,
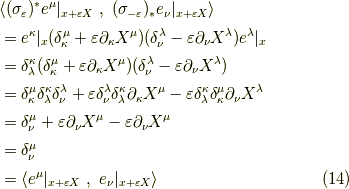
となります.ここでも, 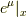 と
と 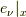 は双対ベクトルであることを使いました.
最初と最後から,
は双対ベクトルであることを使いました.
最初と最後から, 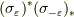 はあっても無くても同じ,つまり,単位行列です.
はあっても無くても同じ,つまり,単位行列です.
今日はここまで.お疲れさまでした.