この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
微分幾何学における流れの具体例
この記事では,リー微分を理解するのに必要な流れの具体例をいくつか見ます.
記法としては,中原幹夫先生の理論物理学のための幾何学とトポロジーIのものを採用します.
以下では二次元平面上の事を考え,ベクトル場を 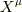 で,積分曲線を
で,積分曲線を 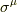 とします.
とします.
すると,

を満たします.
例1
ベクトル場
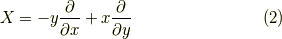
あるいは,同じことですが,
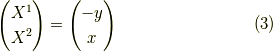
に対して,積分曲線は
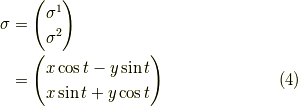
と書けます.
すると,
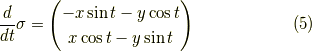
であり,一方,
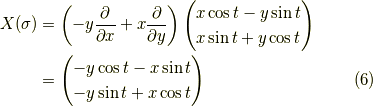
だから,
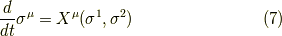
が確かに成り立っています. 与えられた 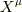 に対する
に対する
 を求めるには,式
を求めるには,式 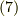 を具体的に書いて,
を具体的に書いて,

で, 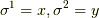 つまり,
つまり, 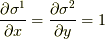 と,
と,  に気が付けば簡単で,
に気が付けば簡単で,
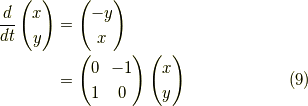
を解けば良いです.
積分曲線は,式 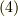 から
から  を消去して,初期位置
を消去して,初期位置 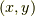 として,
として,
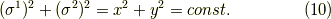
となります.つまり,積分曲線は同心円となります.
例2
例1と同様なので,要点だけ書きます.
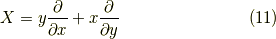

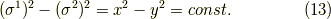
これは双曲線です.
例3
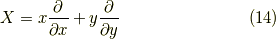

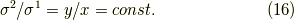
または,

これは原点を通る直線です.
例4
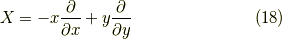

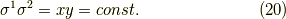
これは双曲線です.
例5

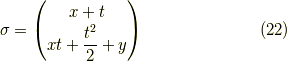
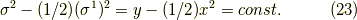
この例は今までのやり方と少し異なる工夫が必要です.
解くべき方程式は,
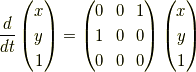
です.ここで,
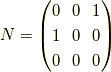
と置きます. すると,解は
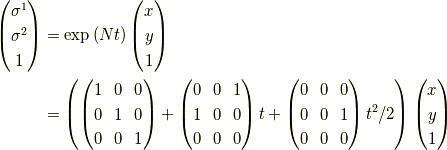
となります.ここで, 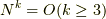 を用いました.
これは放物線です.
を用いました.
これは放物線です.
この記事の内容を踏まえて,次回,リー微分について書こうと思います. 今日はここまで.お疲れさまでした.