この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
整域・整数の剰余類の環
整数の全体が環になることは 環 の例で見ました.整数の環を 整数環 と呼ぶのでした.整数環の勉強には,素因数分解,合同など,整数ならではの知識がどうしても必要になってきます.
この記事の最後に整数の剰余類の環について勉強しますが,そこで,二つの整数 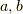 とその最大公約数
とその最大公約数 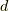 に対し,次の関係式を満たす整数
に対し,次の関係式を満たす整数 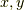 が必ず一組存在することを使います.
が必ず一組存在することを使います.

このような 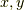 を探す問題はディオファントス方程式と呼ばれ,必ず解が一意的に決まることが知られていますが,ここでは解の存在証明は省略します(ゴメンナサイ (>_<)).
を探す問題はディオファントス方程式と呼ばれ,必ず解が一意的に決まることが知られていますが,ここでは解の存在証明は省略します(ゴメンナサイ (>_<)).
二つの整数 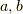 の最大公約数
の最大公約数 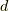 は,
は, 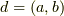 という記号で書くことにします.
という記号で書くことにします. 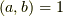 となるとき aとbは互いに素である といい,自分より小さな全ての整数と互いに素になる整数を 素数 と呼びます.
となるとき aとbは互いに素である といい,自分より小さな全ての整数と互いに素になる整数を 素数 と呼びます.
整域
整数環に関係深い概念に 整域 があります.整域の定義は,『可換環で,単位元を持ち,零元以外に零因子を持たない環』です.
整域の例として重要なのは, 整数環 と 多項式環 です.
整数環
整数環とは,普通の整数全体のことです.さきほど見たように,普通の意味で整数の足し算・掛け算を考えることで整数全体は環となります.整数の掛け算は可換です.しかも単位元 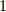 を持ち,零因子はありません.
を持ち,零因子はありません.
ですから,整数環は整域になるわけです.
| [*] | 整域という名前から分かるように,そもそも整域とは,整数の性質を念頭に置いて考え出された概念です. |
多項式環
実数係数の多項式全体は,通常の加法と乗法に関して可換環になります.(これを 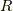 上の多項式環と呼び,以後
上の多項式環と呼び,以後 ![R[x]](http://hooktail.maxwell.jp/kagi/c5b845aa2373916b6d15dbfe5ce5aae3.png) と書きます.
と書きます. 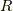 は,実数体の意味です.)
は,実数体の意味です.)
次の二つの多項式に対し,加法と乗法がなりたつことを確認してみてください.
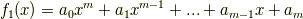
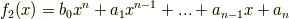
多項式環の単位元は 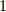 です.また
です.また 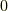 以外に零因子はありません.(もし多項式環に零因子があるならば,
以外に零因子はありません.(もし多項式環に零因子があるならば, 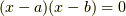 という形に因数分解して方程式を解くことが出来なくなります).
という形に因数分解して方程式を解くことが出来なくなります).
多項式環は整域になります.
体
体では乗法の逆演算として除法が定義されていますので,乗法の零元以外には零因子を持ちません.また,体は単位元を持ち,体の乗法は可換と定義されていました.そこで, 体も整域だ と考えることができます.
整数の剰余類
整数環 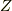 は加法に関しては群になります.この加法群
は加法に関しては群になります.この加法群 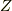 の整数
の整数 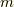 による剰余群を考えます(
による剰余群を考えます( ![[k]](http://hooktail.maxwell.jp/kagi/d67a02e18721ce594223364f961c793e.png) は
は 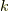 の倍数を含む剰余類という意味です).
の倍数を含む剰余類という意味です).
![Z/[m]= \{[0],[1],...,[m-1]\}](http://hooktail.maxwell.jp/kagi/40910b86884bb48c95ce8c8f97c3aed1.png)
整数 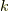 は
は ![[0],[1],...,[m-1]](http://hooktail.maxwell.jp/kagi/2f82eeb4255aefd04f2294743c1d90e9.png) のうちのどれかに属するはずですが,いま仮に
のうちのどれかに属するはずですが,いま仮に 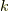 を含む剰余類を
を含む剰余類を 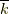 と書くことにすると,すでに 体 の例6で見たように,剰余類の間に加法と乗法を定義できます.
と書くことにすると,すでに 体 の例6で見たように,剰余類の間に加法と乗法を定義できます.
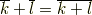
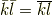
ここで 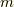 を素数ではないとすると,
を素数ではないとすると, 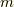 は
は 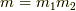 のように素因数分解できるはずです.このとき
のように素因数分解できるはずです.このとき 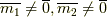 ですが,
ですが, 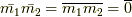 がなりたちますので
がなりたちますので 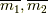 はそれぞれ互いに零因子であり,
はそれぞれ互いに零因子であり, ![Z/[m]](http://hooktail.maxwell.jp/kagi/fa65398190892708e25c3815bd5b2e1b.png) は整域ではなくなります.
は整域ではなくなります.
逆に, 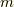 が素数のとき,
が素数のとき, 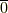 以外の剰余類に属する元
以外の剰余類に属する元  に対して常に
に対して常に 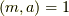 がなりたちます.そこで式
がなりたちます.そこで式 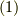 より
より 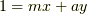 を満たす整数
を満たす整数 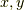 が存在しているはずで,剰余を考えると次式が示されます.
が存在しているはずで,剰余を考えると次式が示されます.
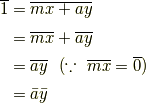
なんとこれは,式中の 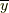 が
が 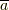 の逆元になっているという主張です.
の逆元になっているという主張です.  は
は 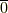 以外の剰余類に属する任意の元でしたので,結局,
以外の剰余類に属する任意の元でしたので,結局, 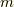 が素数の場合は乗法に逆元も存在することになり,
が素数の場合は乗法に逆元も存在することになり, ![Z/[m]](http://hooktail.maxwell.jp/kagi/fa65398190892708e25c3815bd5b2e1b.png) は体になります.(もちろん
は体になります.(もちろん ![Z/[m]](http://hooktail.maxwell.jp/kagi/fa65398190892708e25c3815bd5b2e1b.png) は整域にもなります.)
は整域にもなります.)
Important
整数の剰余類の環 ![Z/[m]](http://hooktail.maxwell.jp/kagi/fa65398190892708e25c3815bd5b2e1b.png) は,
は, 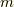 が素数でない場合には零因子が存在し,整域にはならない.(単なる環).
が素数でない場合には零因子が存在し,整域にはならない.(単なる環). 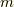 が素数の場合は,整域になり,乗法に逆元が入るので体になる.
が素数の場合は,整域になり,乗法に逆元が入るので体になる.
整数の剰余環は,法とする整数が素数かどうかで,かなり構造が違ってくるんですね.