この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
標準反応エンタルピーと標準エントロピー及び標準反応ギブズエネルギー
私が大学の教養課程において,これが分からず化学系に行くのを断念しました [*] . 同じ轍を踏む人がいないようにこの記事を書きます. これは,熱化学表の見方を勉強しようというものです.
| [*] | そう,ある意味,だから僕は物理系なのよ. |
エンタルピー
エンタルピー 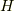 とは,次のような量です.
とは,次のような量です.

ただし 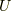 は系の内部エネルギー,
は系の内部エネルギー, 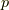 は圧力,
は圧力, 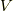 は体積です.
ここで熱力学第一法則を微分形で書くと,
は体積です.
ここで熱力学第一法則を微分形で書くと,

よって,エンタルピーの微分形は,
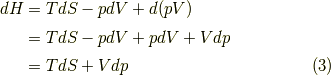
エンタルピーは定圧変化において威力を発揮します.
化学反応が起きて,気体が発生したとしましょう.
内部エネルギー変化 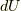 は
は 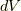 を含むので気体の体積変化を考慮しなければなりません.
を含むので気体の体積変化を考慮しなければなりません.
しかし,エンタルピー変化は定圧条件 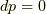 の元では,
エントロピーの微分形の定義,
の元では,
エントロピーの微分形の定義,

つまり [†] ,
| [†] | 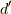 は不完全微分を表すのでした.反応の始点と終点が共通でも,この不完全微分の量は反応経路により,
変わってきます.状態量にはなりえないのです. は不完全微分を表すのでした.反応の始点と終点が共通でも,この不完全微分の量は反応経路により,
変わってきます.状態量にはなりえないのです. |

より,

となり,状態量 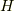 の変化量
の変化量 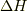 で出入りする熱量
で出入りする熱量 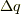 が表現できるのです.
が表現できるのです.
特に反応の始点と終点が共に標準状態(その物質のある温度における圧力 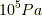 の下での純粋な形で存在する状態です.)
の時に,出入りする熱量を標準反応エンタルピー
の下での純粋な形で存在する状態です.)
の時に,出入りする熱量を標準反応エンタルピー 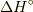 と言います.これは,
高校までの化学において,反応熱と言う概念がありましたが,それの符号を変えたものが標準反応エンタルピー
だと考えて良いと思います.「符号を変える」とは,どういうことかというと,エンタルピーは,メタンなどのようにエネルギーをたくさんもっている物質では高く,二酸化炭素のようにエネルギーをあまりもっていない物質では,低いからです.
メタンが酸素と反応(燃焼)して,どれだけエネルギーを減らしたかが反応エンタルピー(
と言います.これは,
高校までの化学において,反応熱と言う概念がありましたが,それの符号を変えたものが標準反応エンタルピー
だと考えて良いと思います.「符号を変える」とは,どういうことかというと,エンタルピーは,メタンなどのようにエネルギーをたくさんもっている物質では高く,二酸化炭素のようにエネルギーをあまりもっていない物質では,低いからです.
メタンが酸素と反応(燃焼)して,どれだけエネルギーを減らしたかが反応エンタルピー( 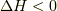 )なのです.
この時,反応熱
)なのです.
この時,反応熱 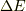 は,どれだけ熱を放出したかでしたので,
は,どれだけ熱を放出したかでしたので, 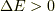 ですね.
この様に,反応熱と反応エンタルピーの符号が反対なのは,よろしいでしょうか?
ちなみにエンタルピーの計算では,反応にかかわる一つの物質
ですね.
この様に,反応熱と反応エンタルピーの符号が反対なのは,よろしいでしょうか?
ちなみにエンタルピーの計算では,反応にかかわる一つの物質 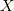 に注目し,それが一モル反応または生成する時のエンタルピーを
用い,標準モルエンタルピー
に注目し,それが一モル反応または生成する時のエンタルピーを
用い,標準モルエンタルピー 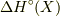 と呼びます.そして,
と呼びます.そして, 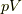 は気体などの生成に際し,圧力をもって外に仕事をする,その仕事まで考えていると言っていいでしょう.
は気体などの生成に際し,圧力をもって外に仕事をする,その仕事まで考えていると言っていいでしょう.
エントロピーとギブズの自由エネルギー
孤立系において,エントロピーは上昇する方向に反応は進行するというのが,熱力学第二法則の言わんとすることでした.
ここで,定圧等温過程を考えます.そして,系 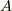 が熱浴
が熱浴 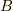 の中に入っている時を考えます.
の中に入っている時を考えます.
エネルギーの保存則から,全体のエンタルピー変化 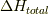 はありませんから,
はありませんから,
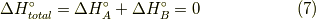
となります. 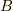 のエントロピー変化は,等温過程なので,
のエントロピー変化は,等温過程なので, 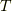 一定より,簡単に計算できて,
一定より,簡単に計算できて,
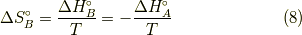
注意して欲しいのは,
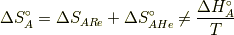
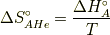
であります.ここで, 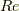 はReactionで反応の,
はReactionで反応の, 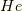 はHeatで,仕事と熱のやり取りのエントロピー変化を
表します.化学反応や混合,相変化などにより,熱のやり取り以上にエントロピーが生成する [‡] のです.
はHeatで,仕事と熱のやり取りのエントロピー変化を
表します.化学反応や混合,相変化などにより,熱のやり取り以上にエントロピーが生成する [‡] のです.
| [‡] | 後の議論を見てもらえれば分かるかと思いますが,エンタルピーの減少する反応や相変化ならば,エントロピーが減少するこ ともあります.例えば,気体同士の反応で,容積が減る反応 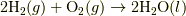 等の反応が挙げられます.熱の移動を含めたエントロピーがトータルで増加する(ギブズエネルギーが減少する)反応が自発的 に起こる反応です. 等の反応が挙げられます.熱の移動を含めたエントロピーがトータルで増加する(ギブズエネルギーが減少する)反応が自発的 に起こる反応です. |
ここで,第二法則よりエントロピーが増える方向にしか反応が進まないので, 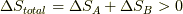 より,
より,
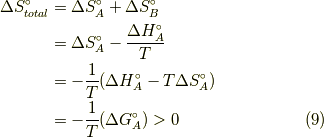
最後の行の 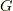 とは,ギブズの自由エネルギー(標準反応ギブズエネルギー)であり,
とは,ギブズの自由エネルギー(標準反応ギブズエネルギー)であり,
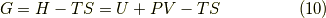
で定義されます.
よって,第二法則より化学反応は,ギブスの自由エネルギーが減少する方向にしか,進まないことが分かりました.
少しこの式の持つ意味を考察してみましょう.低温では, 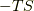 が小さいので反応エンタルピーが反応方向の決定に
大きな影響を及ぼします.逆に高温だと,
が小さいので反応エンタルピーが反応方向の決定に
大きな影響を及ぼします.逆に高温だと, 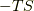 は負の大きな値をもつので,反応のエントロピー変化が,
大きな影響を及ぼすことになります.
は負の大きな値をもつので,反応のエントロピー変化が,
大きな影響を及ぼすことになります.
ちなみに,物質のエントロピーの計算は面倒ですが,熱力学第三法則(絶対零度において物質のエントロピーはゼロに等しい.) を利用して計算するようです.
以上で,熱化学表を読むことができるようになるための, 基礎論を終了します.今日は,ここまで.お疲れ様でした.