この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
実格子と逆格子の対応
ここでは物性物理をされている方の大半が悩むものであろう実格子(直接格子)と 逆格子の対応について考えていきます.単刀直入に言って, この二つは点と面の対応(二次元なら点と線の対応)だったのです. 点と点の対応を探しても分からないはずです. では,見ていきましょう.
実格子とは
実格子ベクトル 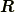 は結晶の基本並進ベクトル
は結晶の基本並進ベクトル 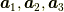 と整数
と整数 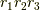 に対して,
に対して,
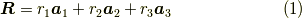
で定義されます.実際の空間中に点が規則正しく並んでいるイメージです.
ここで,全ての実格子の点の集合を  とおきます.
とおきます.
つまり,
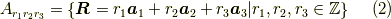
です.また,今後の展開の為,係数  を実数化したものを
を実数化したものを  とします.
とします.
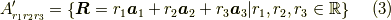
という事です.
逆格子とは
今度は逆格子です.どう定義されるかと言うと,
式 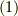 で定義される全ての実格子ベクトルに対して以下が成立するベクトルの事です.
で定義される全ての実格子ベクトルに対して以下が成立するベクトルの事です.

これを求めるには,基本並進ベクトルを用いて以下の基本逆格子ベクトル  を考えます.
を考えます.
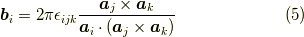
ここで, 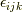 は完全反対称テンソル(エディントンのイプシロン)です.
すると,クロネッカーのデルタ
は完全反対称テンソル(エディントンのイプシロン)です.
すると,クロネッカーのデルタ 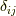 を用いて,
を用いて,

という関係が成立します.
すると,逆格子ベクトルは,整数 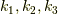 を用いて以下の様に定義されます.
を用いて以下の様に定義されます.
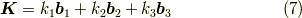
式  同様に,逆格子の全ての点の集合を
同様に,逆格子の全ての点の集合を 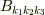 とします.つまり,
とします.つまり,
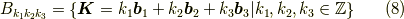
です.また,係数 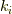 を実数化したものを
を実数化したものを 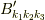 とします.
とします.

という事です.
逆格子の点と実格子の直線群の対応の具体例
ここから,簡単の為二次元に話を制限しましょう.
これは式 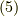 に於いて,
に於いて,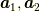 をxy平面内の
ベクトル,
をxy平面内の
ベクトル, 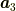 を
を  方向を向いたベクトル
方向を向いたベクトル 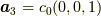 として,
考えれば良いです.ここで,実格子ベクトルの次元(m:メートル)を考慮して,
格子定数
として,
考えれば良いです.ここで,実格子ベクトルの次元(m:メートル)を考慮して,
格子定数 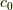 を設定してあります.
を設定してあります.
ここでは具体的な逆格子空間中の点を一つ選んで,実格子のどの直線に当たるかを考えます.
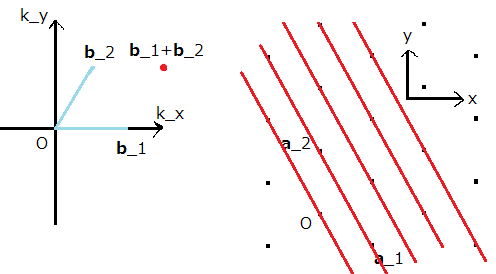
まず,六方格子を考え実格子空間を以下の様に定めます. 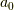 も長さの次元を持つ定数です.
も長さの次元を持つ定数です.
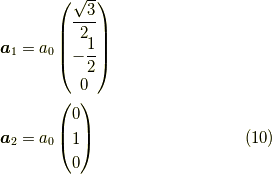
とします.
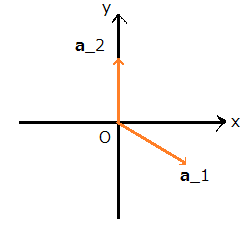
すると,基本逆格子ベクトルは以下の様になります.
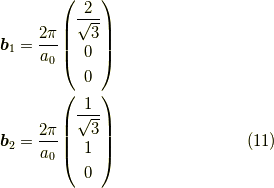
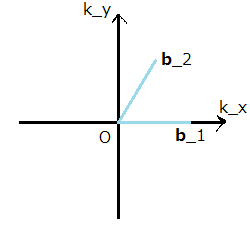
対応1
ここで,点 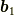 に対応する面を見てみましょう.
に対応する面を見てみましょう.
式 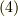 の再掲をして,
の再掲をして,

これの意味するところは,整数  として,
として,

となります.式 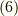 からこの左辺は簡単に求まり,
からこの左辺は簡単に求まり,
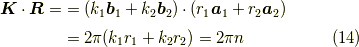
となります.今, 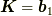 つまり
つまり 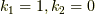 が対応する実空間の部分を求めたいのです.
それは,
が対応する実空間の部分を求めたいのです.
それは,
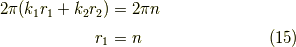
ここで,  は任意の整数でしたから,これは直線群
は任意の整数でしたから,これは直線群 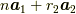 です.
ここで,
です.
ここで, 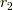 は任意の実数です.図にすると以下の様になります.
は任意の実数です.図にすると以下の様になります.
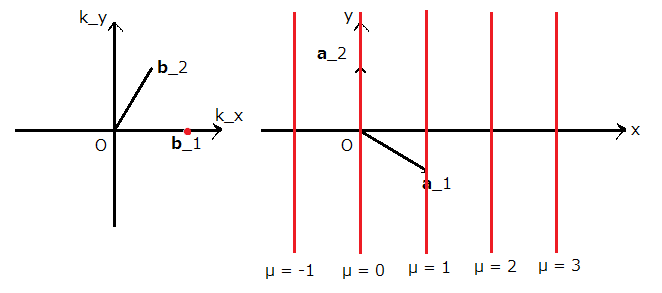
対応2
また,今度はその一つ隣の 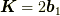 つまり
つまり  を考えましょう.
を考えましょう.
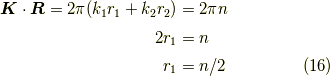
となるので,今度はさっきの直線群の間隔が半分になったものです.
対応3
今度は 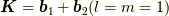 の対応する直線群を求めましょう.
の対応する直線群を求めましょう.

これは直線群
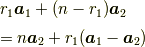
です.これは 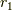 が任意の実数なので,
が任意の実数なので, 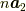 を
通り
を
通り  に平行な直線群です.
に平行な直線群です.
対応4(逆格子空間の逆格子点以外の点)
ここまでは逆格子空間の逆格子点と実空間の対応を見てきました. 更には,逆格子空間の逆格子点以外の点も対応がある事にお気づきでしょうか?
例えば, 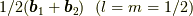 の時は,
の時は,

もう図は書きませんが,これは 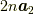 を
通り
を
通り  に平行な直線群です.
間隔が対応3の時の倍の実空間の直線群となりますね.
に平行な直線群です.
間隔が対応3の時の倍の実空間の直線群となりますね.
完全な対応(格子点の集合と集合の対応)
ここまでは逆格子の点と平面群の対応の話でした.
しかし,逆「格子」と言うからには,
一定の規則を持って整列した点の集合の対応物こそが,
重要な意味を持っているはずです.それを見てみます.
実はこの為に 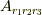 や
や 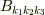 を用意したのです.
を用意したのです.
ここで逆格子の点 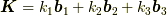 に対して,
対応する実格子の平面群を以下の様に名づけます.
に対して,
対応する実格子の平面群を以下の様に名づけます.
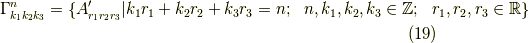
例えば, 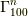 ならば,対応1で求めた直線群を三次元に拡張した
ならば,対応1で求めた直線群を三次元に拡張した 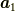 に
垂直な平面群です.
に
垂直な平面群です. 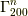 ならば,対応2で求めた直線群を三次元に拡張した,
先ほどの半分の周期の
ならば,対応2で求めた直線群を三次元に拡張した,
先ほどの半分の周期の 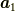 に垂直な平面群です.
に垂直な平面群です.
僕が主張したいことは,
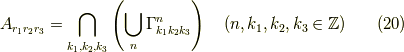
ではないかという事です.
つまり,言葉で表現すると,
まず特定の 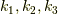 を持つ
を持つ  が異なる平面の集合を一つの図形
が異なる平面の集合を一つの図形 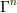 と考えます.
(今,
と考えます.
(今, 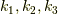 を固定しているので添え字を省略した.)
そして,その後異なる
を固定しているので添え字を省略した.)
そして,その後異なる 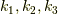 に対して,その
に対して,その 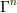 の共通部分を求めると,
実格子の格子点となっているだろうという事です.
の共通部分を求めると,
実格子の格子点となっているだろうという事です.
すみませんが,式 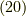 は証明はできていません.
しかし,今まで具体的に見てきたように,
は証明はできていません.
しかし,今まで具体的に見てきたように, 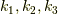 が整数の組だった場合,実格子の上を
平面群
が整数の組だった場合,実格子の上を
平面群 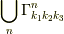 が漏らさず通る事から,
ほぼ確実に成立するだろうと思います.
が漏らさず通る事から,
ほぼ確実に成立するだろうと思います.
さらに言えば,
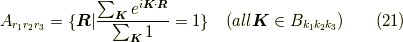
も成立するでしょう.なぜなら,格子点では 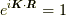 が成立するので,式
が成立するので,式  の分数の値は
の分数の値は 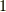 となります.しかし,それ以外の点では,複素数の指数関数の位相がゼロではなくなり,その
となります.しかし,それ以外の点では,複素数の指数関数の位相がゼロではなくなり,その  倍周期を足していくことによって,ゼロになるはずです.
倍周期を足していくことによって,ゼロになるはずです.
それでは今日はこの辺で,お疲れ様でした.