この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
gradの積分形による定義
はじめに, 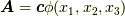 という形のベクトル場を考えてみます.ここで
という形のベクトル場を考えてみます.ここで  は任意の定ベクトル,
は任意の定ベクトル, 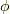 は適当な
は適当な  級のスカラー関数であるとします.このベクトル場に対して,ガウスの発散定理を使ってみましょう.
級のスカラー関数であるとします.このベクトル場に対して,ガウスの発散定理を使ってみましょう.

ただし,式中, 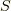 はある閉曲面,
はある閉曲面,  は
は 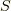 によって囲まれる領域とし,
によって囲まれる領域とし, 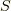 には外向きを正とする向きが与えられており,その単位法線ベクトルを
には外向きを正とする向きが与えられており,その単位法線ベクトルを 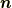 としています.(
としています.( 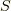 は向きを定義できる曲面だとしています.)
は向きを定義できる曲面だとしています.) 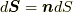 として,式
として,式 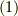 を次のように変形します.
を次のように変形します.
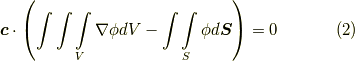
式  で
で  は任意のベクトルなので,
は任意のベクトルなので,  に関わらず,式
に関わらず,式  が成り立つためには,括弧部分
が成り立つためには,括弧部分  となることが要請されます.
となることが要請されます.
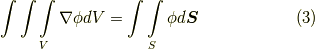
ここで,左辺の中身は 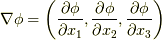 ですが,例えばこの第一成分の積分だけに注目してみましょう.
ですが,例えばこの第一成分の積分だけに注目してみましょう.

ここで,式  の積分について中間値の定理を用いると,領域
の積分について中間値の定理を用いると,領域  内のどこかに,次式を満たす点
内のどこかに,次式を満たす点  が存在することが保証されます.(右辺の括弧の下に
が存在することが保証されます.(右辺の括弧の下に 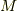 とあるのは,『点
とあるのは,『点 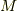 における値』という意味です.)
における値』という意味です.)
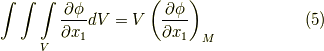
| [*] | 中間値の定理に馴れていない人のために補足説明しておきます.領域  内の各点で 内の各点で 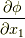 は色々な値を取ります.大きい値や小さい値など色々ですが,その平均値の大きさは,必ず最大値と最小値の間に来ることでしょう.ですから, は色々な値を取ります.大きい値や小さい値など色々ですが,その平均値の大きさは,必ず最大値と最小値の間に来ることでしょう.ですから, 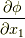 の変化が連続ならば,色々な の変化が連続ならば,色々な 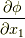 の値の平均値を与えるような点が,必ず の値の平均値を与えるような点が,必ず  の中のどこかに存在するはずだと考えられます.体積分とは,一般に場所によって値の異なる関数 の中のどこかに存在するはずだと考えられます.体積分とは,一般に場所によって値の異なる関数 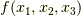 に対し, に対し, 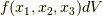 の形を全体で足し合わせた量ですが,これは『 の形を全体で足し合わせた量ですが,これは『 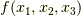 の平均値 の平均値  』に等しくなるはずです.(それが平均値の定義だからです.)式 』に等しくなるはずです.(それが平均値の定義だからです.)式  の変形は,そんな意味です. の変形は,そんな意味です. |
式  を 式
を 式 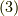 の左辺に代入すると,第一成分について次式を得ます.
の左辺に代入すると,第一成分について次式を得ます.
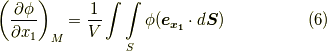
次に,  内の任意の一点
内の任意の一点 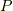 を考えます.一般に
を考えます.一般に 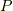 と
と 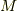 は異なる点ですが,
は異なる点ですが,  を
を 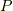 に向けて縮めていくと,それにつられて
に向けて縮めていくと,それにつられて 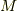 も
も 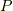 に近づいてくるはずです.(というのは,領域
に近づいてくるはずです.(というのは,領域  において
において 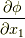 は連続だと仮定しているからです.)
は連続だと仮定しているからです.)

領域を一点 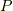 に狭めていけば,平均値を与える点
に狭めていけば,平均値を与える点 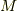 も
も 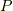 に近づいていく.
に近づいていく.
そこで,  内の任意の一点
内の任意の一点 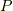 に対して,次式が成り立ちます.
に対して,次式が成り立ちます.
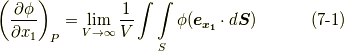
同様にして, 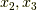 成分についても次式が成り立ちます.
成分についても次式が成り立ちます.
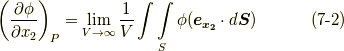
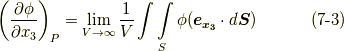
式  を足すことで,次式を得ます.これが,積分形による勾配(
を足すことで,次式を得ます.これが,積分形による勾配(  )の表現です.領域
)の表現です.領域  内の点ならば,どこでもこの形で勾配を表現できますので,わざわざ
内の点ならば,どこでもこの形で勾配を表現できますので,わざわざ  と書くのはやめます.
と書くのはやめます.
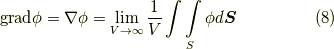
右辺の極値が本当に存在するかどうかについて,細かな議論をしませんでしたが,領域が単連結で, 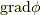 が連続であるならば右辺は収束すると考えて良いでしょう.( 単連結 でなければ,任意の点に領域全体を収束させることは出来ません.)この形をじっと見ていると,右辺が一切座標系の取り方と関係ない形になっていることに気づきます.つまり,
が連続であるならば右辺は収束すると考えて良いでしょう.( 単連結 でなければ,任意の点に領域全体を収束させることは出来ません.)この形をじっと見ていると,右辺が一切座標系の取り方と関係ない形になっていることに気づきます.つまり, 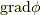 は座標系の取り方に寄らない表現だということです.
は座標系の取り方に寄らない表現だということです.
Important
勾配 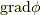 は,座標系の取り方によらない.
は,座標系の取り方によらない.
これは非常に素敵な性質です♪ もし,何かの関係式(例えば物理法則)が 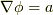 (
(  はスカラー関数)のような形で表現されるとすれば,この式はどんな座標系でも成り立ってしまうということです.
はスカラー関数)のような形で表現されるとすれば,この式はどんな座標系でも成り立ってしまうということです.
| [†] | ただし,式自体はどの座標系でも成り立ちますが,それは定式化を座標系と無関係に行ったという意味であって,実際に  を微分演算子とみて,各成分毎に微分しようと思えば,やはり何か座標系を決めなければなりません. を微分演算子とみて,各成分毎に微分しようと思えば,やはり何か座標系を決めなければなりません.  という形は,いわば『お好きな座標系をお選び下さい』と言っているようなもので,ひとたび座標系を決めれば,その表現が座標変換に対して不変になっているという意味ではありません.( ベクトルの関数 や 積分定理のまとめと展望 にも類似した註を書いたので,参考にして下さい.) という形は,いわば『お好きな座標系をお選び下さい』と言っているようなもので,ひとたび座標系を決めれば,その表現が座標変換に対して不変になっているという意味ではありません.( ベクトルの関数 や 積分定理のまとめと展望 にも類似した註を書いたので,参考にして下さい.) |
電磁気学や流体力学には  を使って表現した物理法則がたくさん出てきますが,このように書いておけば,どんな座標系にも適用できる普遍的な表現になる,というのがセールスポイントです.
を使って表現した物理法則がたくさん出てきますが,このように書いておけば,どんな座標系にも適用できる普遍的な表現になる,というのがセールスポイントです.