この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。 リンクを正しく張れていないところが存在しますのでご注意ください。 正式公開まで、いましばらくお待ちください。
全角運動量

剛体の回転シーリズ第４弾です． 前の記事は 角運動量を持つ系の例 です． 次の記事は 慣性モーメント です．

全角運動量の時間依存性

多くの質点からなる系 [*] を考えます． この系に含まれる質点全体がもつ運動量の合計を求めます． それぞれの質点の持つ角運動量は，ベクトル量なので足し合わせることができます． 質点の位置を 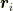\bm{r}_i とし，ある点 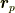\bm{r}_p の周りの角運動量を考えれば全角運動量は，

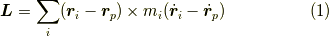
\bm{L}&=\sum_i(\bm{r}_i-\bm{r}_p)\times m_i (\dot{\bm{r}}_i-\dot{\bm{r}}_p) \tag{1}

となります．

[*]余談ですが，私がはじめ数学で系という単語を聞いた時，何のことなのかよく分かりませんでした．でも英語でsystemというとなんとなくわかったような気になりませんか？言いたかったのはこれだけです．今現在までそれ以上の理解はしていませんでした．しかし，思い切って広辞苑で調べてみました．数学でいう「系」という言葉の意味は，「ある定理からたやすく推定しうる命題」のことだそうです．結局，systemと言い換えても得られるものは何もないというオチでした．分らないことは調べましょうというのが教訓でしょうか．

今この量の時間変化を考えたいので，式 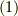(1) の時間微分をとると，

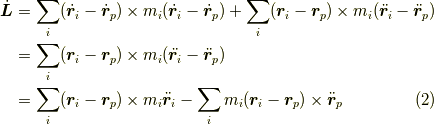
\dot{\bm{L}}&=\sum_i(\dot{\bm{r}}_i-\dot{\bm{r}}_p)\times m_i(\dot{\bm{r}}_i-\dot{\bm{r}}_p)+\sum_i(\bm{r}_i-\bm{r}_p)\times m_i(\ddot{\bm{r}}_i-\ddot{\bm{r}}_p) \\&= \sum_i(\bm{r}_i-\bm{r}_p)\times m_i(\ddot{\bm{r}}_i-\ddot{\bm{r}}_p) \\&= \sum_i(\bm{r}_i-\bm{r}_p)\times m_i\ddot{\bm{r}}_i - \sum_im_i(\bm{r}_i-\bm{r}_p) \times \ddot{\bm{r}}_p \tag{2}

となります．

ここで，式 (2) の第一項に質点iに働く外力を \bm{F}_i^{\rm{\rm{ext}}} ，内力を \bm{F}_i^{\rm{int}} と表した運動方程式

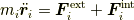
m_i \ddot{\bm{r}}_i =\bm{F}_i^{\rm{ext}} + \bm{F}_i^{\rm{int}}

を用いれば，

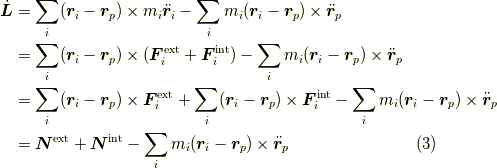
\dot{\bm{L}} &= \sum_i(\bm{r}_i-\bm{r}_p)\times m_i\ddot{\bm{r}}_i - \sum_im_i(\bm{r}_i-\bm{r}_p) \times \ddot{\bm{r}}_p \\&= \sum_i(\bm{r}_i-\bm{r}_p)\times (\bm{F}_i^{\rm{ext}} + \bm{F}_i^{\rm{int}}) - \sum_im_i(\bm{r}_i-\bm{r}_p) \times \ddot{\bm{r}}_p \\&= \sum_i(\bm{r}_i-\bm{r}_p)\times \bm{F}_i^{\rm{ext}} + \sum_i(\bm{r}_i-\bm{r}_p)\times \bm{F}_i^{\rm{int}} - \sum_im_i(\bm{r}_i-\bm{r}_p) \times \ddot{\bm{r}}_p \\&= \bm{N}^{\rm{ext}} + \bm{N}^{\rm{int}} - \sum_im_i(\bm{r}_i-\bm{r}_p) \times \ddot{\bm{r}}_p \tag{3}

今度は，

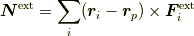
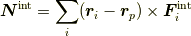
\bm{N}^{\rm{ext}} = \sum_i(\bm{r}_i-\bm{r}_p)\times \bm{F}_i^{\rm{ext}} \bm{N}^{\rm{int}} = \sum_i(\bm{r}_i-\bm{r}_p)\times \bm{F}_i^{\rm{int}}

は，それぞれpの周りの全外力，全内力によるトルクです．

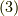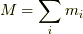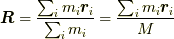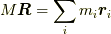それから，式 (3) の第二項も変形していきます．全質量 M=\sum_i m_i ， 重心 \bm{R}= \frac{\sum_i m_i \bm{r}_i}{\sum_i m_i} = \frac{\sum_i m_i \bm{r}_i}{M} を用いて， M\bm{R}= \sum_i m_i \bm{r}_i ですから，

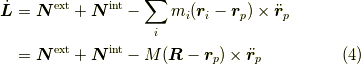
\dot{\bm{L}}&= \bm{N}^{\rm{ext}} + \bm{N}^{\rm{int}} - \sum_i m_i(\bm{r}_i-\bm{r}_p) \times \ddot{\bm{r}}_p \\&= \bm{N}^{\rm{ext}} + \bm{N}^{\rm{int}} - M(\bm{R}- \bm{r}_p) \times \ddot{\bm{r}}_p \tag{4}

だいぶ，すっきりしてきました． さて，ここで多くの質点の中の二点，質点aと質点bに働く内力について考えてみます． 質点bが質点aに及ぼす力を \bm{F}_a^{[ b ]} と書くことにすると， ニュートン第三法則により，

\bm{F}_b^{[ a ]} = - \bm{F}_a^{[ b ]}

が成立します．

そこで，この二点からの全トルク 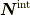\bm{N}^{\rm{int}} への寄与 \bm{N}^{[ a,b ]} を考えてやると，

\bm{N}^{[ a,b ]} &= (\bm{r}_a-\bm{r}_p) \times \bm{F}_a^{[ b ]}+ (\bm{r}_b-\bm{r}_p) \times \bm{F}_b^{[ a ]} \\&= (\bm{r}_a-\bm{r}_p) \times \bm{F}_a^{[ b ]}- (\bm{r}_b-\bm{r}_p) \times \bm{F}_a^{[ b ]} \\&= (\bm{r}_a-\bm{r}_p) \times \bm{F}_a^{[ b ]}+ (\bm{r}_p-\bm{r}_b) \times \bm{F}_a^{[ b ]} \\&= (\bm{r}_a-\bm{r}_b) \times \bm{F}_a^{[ b ]}

となります．この値についてよく考えると， 現在までに見つかっている粒子の力の及ぼし方は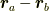， \bm{r}_a-\bm{r}_b と \bm{F}_a^{[ b ]} が 平行なものしかありませんから [†] ，これは平行なベクトル同士の外積ということになり，二粒子間の内力の寄与はゼロになります． よって，すべての二点間の内力について成り立ちますから，結局，内力の全角運動量への寄与はゼロです．

[†]これは十分正しい仮定だといえます．なぜなら粒子が及ぼす力が二点を始点，終点とするベクトルに平行でないとき，空間の一方だけが特別な意味を持ってしまいますよね．粒子の対称性を考えるとこんな事はありえません．方向が対称でない双極子などでも分解した単極子同士の関係に持ち込めますから，結局はこの仮定に帰着できることになります．（そういえば，磁気双極子は磁気単極子に分解できませんよね．正直言うと，はたしてこの仮定が成り立つのかどうかわかりませんでした．でも双極子同士の関係は電気でも磁気でも同じなので，やはり仮定は成り立つのだろうというのが僕の一応の結論です．）

さて，

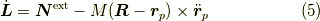
\dot{\bm{L}}&= \bm{N}^{\rm{ext}} - M(\bm{R}- \bm{r}_p) \times \ddot{\bm{r}}_p \tag{5}

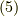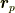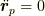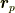という所まで，変形出来ました． 式 (5) の第二項は， \bm{r}_p が一定の速度で移動する点の時（ \ddot{\bm{r}}_p=0 の時）や \bm{r}_p が重心に一致するとき等のように 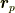\bm{r}_p の取り方として常識的な取り方をした時に，

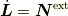
\dot{\bm{L}}&= \bm{N}^{\rm{ext}}

となることが分りました．

つまり全角運動量の変化は，外力によるトルクのみを考えればいいのです． そして，これから書くことは重要なので覚えておいてください．

特に外力がないときは，ある慣性系内の固定点からみた系の全角運動量，または，重心からみた系の全角運動量は保存するわけです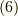． \tag{6}

実例としては，ひとつ前の記事で書いた二つの例を考えてみてください．（元々，前の記事の例を説明するためにこの記事を書いたのでした．） まず一つ目の自由に空間を移動する一粒子の例ですが，一粒子なので重心からみても何も起こらずつまりませんね． 確かに，角運動量は保存します． 次に，ある慣性系内の一点から見てみると，粒子の 速度が変わるわけです．どんな速度でも角運動量は保存しましたから（もちろん，みる慣性系によって初期値は変わってきますが），確かに 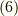(6) は成り立ちます．

そして次の二粒子がたがいに回転し合っている例ですが，重心から見た場合，重心の周りをずっと二粒子が回転し続けることになります． 角運動量が保存されることが分ります．次にある慣性系内の固定点から見た時ですが，これは重心の初速度を変化させることで， 再現できます．これも角運動量が保存されることがわかります．

残念ながらこれ以上例をあげようとしても，三粒子になると多体問題になってしまい解析的には解けませんので，この辺で勘弁してください (^^;

全運動量と全角運動量

全運動量と全角運動量には興味深い違いがあります． 系にかかる外力がゼロの時，全運動量や全角運動量は保存されるわけです． このとき系の内力や内部運動がどうあろうとも，重心は固定されていれば （全運動量がゼロなら），その後重心の位置は変化しません． しかし，全角運動量はゼロであっても，体系は任意の向きを向くことが可能です．

たとえば両手におもりを持って自由に回転できるイスに座ります． 最初は手を降ろしています．次に 手を広げておもりを中心が自分にあり床に平行な円上を反時計方向に回します． すると全角運動量は保存しますから，自分自身は時計方向に回ります． そこで手を降ろすと最初の状態に戻るわけです． これを繰り返せば任意の方向を向くことができます．

続きは， こちら