この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
数体の階層
実数は有理数と無理数に分けられますから,有理数体 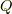 が実数体
が実数体 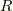 の部分体になっていることは直観的に明らかでしょう.また,実数は複素数の虚部が零である特別な場合ですから,実数体
の部分体になっていることは直観的に明らかでしょう.また,実数は複素数の虚部が零である特別な場合ですから,実数体 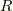 が複素数体
が複素数体 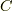 の部分体になっていることも明らかだと思います.
の部分体になっていることも明らかだと思います.
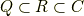
この記事では,このような体の包含関係をもう少し詳しく考えてみます.
代数的数と超越数
すでに 代数的数と超越数 の記事でも触れましたが,有理係数の,つまり 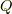 上の代数方程式
上の代数方程式 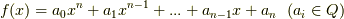 の解として得られる数を 代数的数 と呼び,逆に,絶対に
の解として得られる数を 代数的数 と呼び,逆に,絶対に 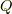 上の代数方程式の解にはならない数を 超越数 と呼びます.
上の代数方程式の解にはならない数を 超越数 と呼びます.
ある数が代数的数であることを示すのは比較的簡単です.たとえば 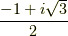 は
は  の解ですから代数的数ですが,このように代数方程式を示せば良いわけです.何度か累乗したり足し引きしたりすれば,意外と簡単に代数方程式を得ることが出来ます.一方,ある数が超越数であることを示すのはとても難しいそうです.
の解ですから代数的数ですが,このように代数方程式を示せば良いわけです.何度か累乗したり足し引きしたりすれば,意外と簡単に代数方程式を得ることが出来ます.一方,ある数が超越数であることを示すのはとても難しいそうです.
有名な超越数には 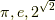 などがあります.方程式論の視点から見ると,このように代数的数と超越数という分類がとても重要です.
などがあります.方程式論の視点から見ると,このように代数的数と超越数という分類がとても重要です.
代数的数の体
代数的数は体になっています.つまり,代数的数で四則演算をすると,その結果も代数的数になるということです.これは非常に感動的な結果ですが,直観的に明らかというわけではないので証明が必要です.証明は少し長くて難しいので,初めてこの記事を読む人は,結果だけを覚えておくだけでも十分だと思います.
theorem
代数的数は体をなします.
proof
代数的数全体の集合を 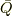 とします.つまり
とします.つまり 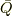 に含まれる数は,何か有理係数代数多項式の零点になっているということです.
に含まれる数は,何か有理係数代数多項式の零点になっているということです. 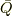 に
に 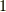 と
と 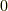 が含まれるのは明らかでしょう(加法と乗法の単位元).また
が含まれるのは明らかでしょう(加法と乗法の単位元).また 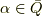 が ある方程式に対して
が ある方程式に対して  を満たすなら
を満たすなら 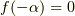 も言えますので,加法の逆元は常に存在することが言えます.また
も言えますので,加法の逆元は常に存在することが言えます.また 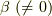 が
が 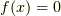 の解であるならば,
の解であるならば, 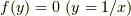 の解は
の解は 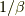 のはずですから,乗法の逆元も存在することが示せました.最後に示すべきことは,代数的数同士の加法と乗法が閉じていることです.そのことの証明を次に述べます(証明の前半).
のはずですから,乗法の逆元も存在することが示せました.最後に示すべきことは,代数的数同士の加法と乗法が閉じていることです.そのことの証明を次に述べます(証明の前半).
proof
いま 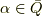 が
が  次方程式
次方程式 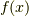 の解であるとき,
の解であるとき, 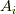 を
を 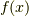 の係数として
の係数として 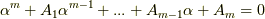 が成り立ちますので,適当な係数
が成り立ちますので,適当な係数 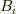 を使って
を使って 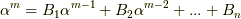 と表わせます.つまり
と表わせます.つまり  の
の  次以上の冪は,常に
次以上の冪は,常に 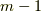 次以下の冪で表わせるということです.同様に,
次以下の冪で表わせるということです.同様に, 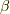 をある
をある  次方程式の解とし,
次方程式の解とし, 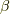 の
の  乗以上の冪は
乗以上の冪は 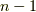 乗以下の冪で表現できるとします.これを使って
乗以下の冪で表現できるとします.これを使って 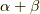 が代数的数になることを示します.
が代数的数になることを示します. 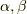 の冪はそれぞれ
の冪はそれぞれ 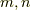 次以下の冪だけで表わされることを使うと,一般に
次以下の冪だけで表わされることを使うと,一般に 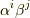 の形は本質的には
の形は本質的には 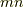 種類しかないと言えます.ここで
種類しかないと言えます.ここで  と考え,
と考え, 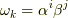 と置くと,一般に
と置くと,一般に 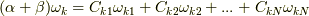 のように表現できるはずです.左辺が右辺のように表わせることは,
のように表現できるはずです.左辺が右辺のように表わせることは, 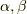 の冪がそれぞれ
の冪がそれぞれ 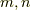 次以下の冪だけで表わされることを再び利用しています.
次以下の冪だけで表わされることを再び利用しています. 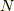 個の
個の 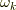 に対してこの方程式を連立すると,行列
に対してこの方程式を連立すると,行列 ![C=[c_{ij}]](http://hooktail.maxwell.jp/kagi/04f94d72da401e91a52ddbc21cf239aa.png) ,ベクトル
,ベクトル 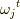 を使い,
を使い, 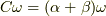 という固有値問題に帰着します.係数
という固有値問題に帰着します.係数 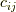 が全て零でないならば,
が全て零でないならば, 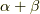 は代数方程式
は代数方程式 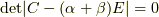 の解になるはずですから,
の解になるはずですから, 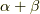 も代数的数だと言えます.全く同じようにして,
も代数的数だと言えます.全く同じようにして, 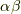 が代数的数であることも示せます.■
が代数的数であることも示せます.■
超越数
一方,超越数の方は,体をなしません.例えば  は超越数ですが,
は超越数ですが,  や
や 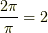 といった計算を考えれば,
といった計算を考えれば,  や
や 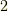 は代数的数ですので,計算が超越数だけで閉じていないことがすぐに示せます.
は代数的数ですので,計算が超越数だけで閉じていないことがすぐに示せます.
また,超越数の超越数乗が,代数的数になる場合もあります.オイラーの公式はその例です.
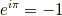
このように,超越数は体にも環にもならず,なかなか計算や証明が素直に行かないため,非常に難しい分野となっているわけです.超越数を,定規とコンパスだけで作図することは出来ません. ギリシャの三大作図問題3 で示したように,作図可能数体は全て有理数体の代数的拡大体になっているからです.
体の包含関係
数の体を,方程式論の立場から,次のように分類してみます.
- 有理数体
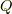
- 作図可能数体
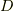
- 有理数体に有理数の
 乗根(無理数)を添加した拡大体
乗根(無理数)を添加した拡大体 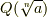
- 代数的数の体
- 複素数体
これらの体の間には,次のような包含関係があることが分かります.
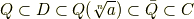
個々の包含関係は,本当なら証明が必要ですがここでは省略します.この包含関係を,しばし眺めて御堪能下さい.拡大体の話がたくさん出てきましたから,一度頭の中でこのような階層構造を整理してみると良いと思います.