この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
空間曲線と接線の方程式
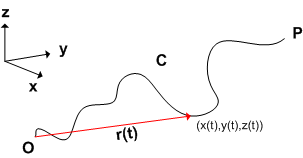
三次元ユークリッド空間内に,一つの曲線 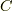 が与えられており,一つの端点を
が与えられており,一つの端点を 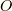 ,もう一端を
,もう一端を 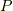 とします.
とします. 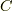 に沿って
に沿って  から
から  に至る曲線の位置ベクトルは,あるパラメーター
に至る曲線の位置ベクトルは,あるパラメーター  を使って式
を使って式  のように表わすことが出来るでしょう.
のように表わすことが出来るでしょう.
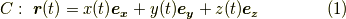
パラメータ  の定義域は適当に調節してやれば,
の定義域は適当に調節してやれば, 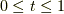 と決めることができます.
と決めることができます. 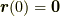 ,
,  となります.
となります.
| [*] | 曲線は一本道ですから,どんなに曲がりくねっていようと曲線上に拘束された点の運動は前へ進むか後ろへ下がるかの二択で,これは一次元的な運動です.これを一つのパラメーターで表現できることが当然と思える人はそれで良いです.しかし,次のような疑問を持つ人もいるかも知れません.『もしも,この曲線が無限の長さを持ち,完全に平面をくまなく埋め尽くしたら,もしくは,くまなく空間を埋め尽くしたら, 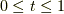 というパラメーターだけで平面や空間の一点を指定できることになってしまう.線分 というパラメーターだけで平面や空間の一点を指定できることになってしまう.線分 ![[0,1]](http://hooktail.maxwell.jp/kagi/ccfcd347d0bf65dc77afe01a3306a96b.png) よりも,平面や空間はずっと"大きい"ような気がするが,はたしてそんな一対一対応は成り立つのだろうか?』こういうことが気になる人は ペアノ曲線 を参照してください. よりも,平面や空間はずっと"大きい"ような気がするが,はたしてそんな一対一対応は成り立つのだろうか?』こういうことが気になる人は ペアノ曲線 を参照してください. |
いま,  を時間と考えれば,
を時間と考えれば, 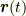 の時間微分は速度を表わすことになります.
の時間微分は速度を表わすことになります.
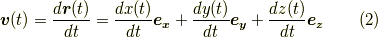
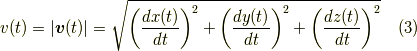
| [†] | パラメーター  は,単なる変数であって,何ら物理的意味を伴う必要はありませんが,力学を連想する文脈で時間だと考えると理解しやすい場合にはそう考えても良いと思います. は,単なる変数であって,何ら物理的意味を伴う必要はありませんが,力学を連想する文脈で時間だと考えると理解しやすい場合にはそう考えても良いと思います.  を時間と考えなければ,式 を時間と考えなければ,式 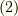 は単に は単に 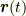 を を  で微分したもの,という味気ないものですが, で微分したもの,という味気ないものですが, 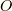 から から 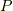 へ移動していく点の運動をイメージしたほうが分かりやすくないでしょうか.実際,力学からの連想でこの関数をしばしば( へ移動していく点の運動をイメージしたほうが分かりやすくないでしょうか.実際,力学からの連想でこの関数をしばしば(  が時間じゃなくても)『速度』と呼ぶことがあります. が時間じゃなくても)『速度』と呼ぶことがあります. |
弧長
空間曲線を表わすパラメーターとして,もう一つ 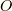 からの移動距離
からの移動距離  を用いる方法があります.動点が
を用いる方法があります.動点が 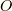 から
から 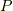 へ移動していく様子をイメージすると,動点が途中で止まったり向きを変えたりしなければ(そのため
へ移動していく様子をイメージすると,動点が途中で止まったり向きを変えたりしなければ(そのため  は単調増加だとします.),
は単調増加だとします.),  と
と  に一対一の対応がつくことが分かると思います.
に一対一の対応がつくことが分かると思います.

力学的に見れば,式 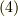 は『速度を時間で積分したら距離になる』という当たり前のことを主張しているだけですが,これを
は『速度を時間で積分したら距離になる』という当たり前のことを主張しているだけですが,これを 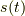 の定義としておきます.今後,曲線を
の定義としておきます.今後,曲線を  ではなく
ではなく  をパラメーターにして考えることも多く,
をパラメーターにして考えることも多く,  を 弧長パラメーター もしくは 標準パラメーター と呼びます.
を 弧長パラメーター もしくは 標準パラメーター と呼びます.
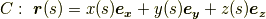
また,微分の略記号も,  による微分に
による微分に  (ダッシュ)を用い,
(ダッシュ)を用い,  による微分には
による微分には  (ドット)を用いて区別することにします.ドットの記号もやはり,
(ドット)を用いて区別することにします.ドットの記号もやはり,  が時間を連想させることに起因する力学からの借用ですね.
が時間を連想させることに起因する力学からの借用ですね.
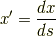

接線の方程式
パラメーターを  から
から  に変更すると嬉しいのは,曲線上の動点の速度が,表面上問題にならなくなるからです.それはどういうことかと言うと,もしも
に変更すると嬉しいのは,曲線上の動点の速度が,表面上問題にならなくなるからです.それはどういうことかと言うと,もしも 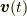 が一定でないと,『
が一定でないと,『 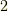 秒進んだときの距離が,
秒進んだときの距離が, 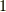 秒進んだときの距離の二倍とは限らない』というような事態が起こってきます.点の運動を考えたいなら,そのような速度の変化にも興味がありますが,曲線の形という幾何学的性質そのものを調べたい場合,どれくらい時間がかかろうと曲線にそって動いてくれれば良いのであって,動点の速度に煩わされたくありません.実際,次のような計算ができます.
秒進んだときの距離の二倍とは限らない』というような事態が起こってきます.点の運動を考えたいなら,そのような速度の変化にも興味がありますが,曲線の形という幾何学的性質そのものを調べたい場合,どれくらい時間がかかろうと曲線にそって動いてくれれば良いのであって,動点の速度に煩わされたくありません.実際,次のような計算ができます.
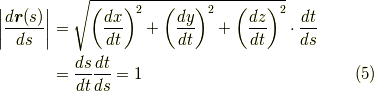
この結果が何を主張しているかというと『  が
が 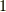 大きくなれば,
大きくなれば, 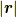 も
も 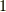 大きくなる』ということです.そもそも
大きくなる』ということです.そもそも  の弧長を
の弧長を  と定義したのですから,これは定義上自明なのですが,とにかく弧長をパラーメーターに取る限り,弧長の変化に対する曲線の変化は常に一定に出来るということです.このあたりに,力学者と幾何学者の興味の微妙なズレがありますね.
と定義したのですから,これは定義上自明なのですが,とにかく弧長をパラーメーターに取る限り,弧長の変化に対する曲線の変化は常に一定に出来るということです.このあたりに,力学者と幾何学者の興味の微妙なズレがありますね.
| [‡] | いま考えているように,曲線や曲面の性質を調べるのに微積分の知識を使う分野を,微分幾何と呼びます.微分幾何の分野では,弧長パラメーターを使って曲線の方程式を考えることが多くなります. |
式 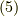 より,
より,  は単位ベクトルだと言えましたので,これを特に
は単位ベクトルだと言えましたので,これを特に 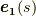 と書くことにします.
と書くことにします. 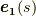 の向きは,曲線が伸びていく方向のはずですから,
の向きは,曲線が伸びていく方向のはずですから, 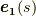 は曲線の 接線ベクトル になります.
は曲線の 接線ベクトル になります.

点 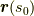 における接線の方程式は,
における接線の方程式は, 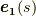 を使って次のように書けることが分かります.
を使って次のように書けることが分かります.
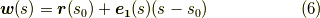
| [§] | 点 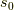 において において  を冪級数展開すると, を冪級数展開すると, 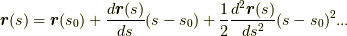 のように書けます.式 のように書けます.式 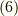 は,この二次以上の項を切り捨てた近似式だと見ることもできます.こう見ると,接線の意味がより明確になるかも知れません. は,この二次以上の項を切り捨てた近似式だと見ることもできます.こう見ると,接線の意味がより明確になるかも知れません. |
以上,ベクトル関数の微分に関係する話題として,空間曲線の接線を取り上げました.