この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
解析力学(ラグランジュ方程式の導出まで)
始めに
みなさんが高校物理で学んだ力学では,自由落下やバネの運動,惑星の運動など様々な運動が運動方程式で語ることができ,自然界の原理のあり方に触れることができました.しかし,現実で起こる現象は運動方程式で解くには難しいものばかりです.そこで登場するのが「解析力学」という考え方です.数式をみると嫌悪感を示す人が多いですが,運動方程式では解くことが難しかった問題も,簡単に扱うことができるという利点があります.この記事では,主にラグランジュ方程式の導出を目標としていきたいと思います.
ラグランジュ方程式とは,下のように表される式のことです.先ほど申し上げたように見た目は運動方程式よりも複雑ですが,現実的な問題を解く際には,ものすごい威力を発揮してくれます.
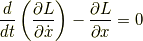
今回の記事では,ラグランジュ方程式の導出までやりたいと思います.初心者向けというよりは,1度自分で勉強した人が見るレベルになっていると思います.また,ハミルトニアンや正準変数等は出てきませんのよろしくお願いします.
1. 解析力学の歴史
まずは,解析力学の歴史からです.幾何光学の分野では, 反射の法則と屈折の法則をまとめ, さらに媒質が連続的に変化している場合にまで拡張した法則として「フェルマーの原理」というものがあります.これは, 「一定点から出て他の一定点に達する光の経路は, 両端を固定したまま途中を連続的に微小変化して得られるすべての経路に比べて, 光がそれを通過するときに要する時間が極小(または極大)になるようなものである」というものです.
要は,光の直進姓を言っています.光は最短距離を進むということです.また, このような法則を一般的に「変分原理」と呼びます.変分原理による力学の定式化は「自然界における現象はその現象が関係する“何かある積分”が極大または極小になるような経路で起こる」という原理で,すべてを説明しようという試みの一環です.
特にこの“何かある積分”を「作用積分」と言います.
簡単に言うと,「フェルマーの原理」で言っている光の直進性を力学分野でも考えてみましょう!という話です.
2. 汎関数
解析力学において,特に変分原理を用いて式を表そうとするとき汎関数の知識が必要になってきます.汎関数とは(2 1)式の様に表される関数であり 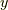 =
=  (
(  )の関数形がどのようなものであるかによって違ってくるものです.
)の関数形がどのようなものであるかによって違ってくるものです.
この時, 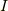 は関数
は関数 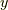 =
=  (
(  )の汎関数であると言い, 一般に
)の汎関数であると言い, 一般に 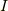 [
[ 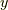 ]という形で表します.関数との違いは,
]という形で表します.関数との違いは,  がある値をとった時に
がある値をとった時に 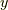 がある値をとるものが関数であるのに対して,
がある値をとるものが関数であるのに対して, 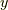 の関数形によって
の関数形によって 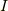 が異なる値をとるものが汎関数であるということです.
が異なる値をとるものが汎関数であるということです.
少し分かりにくいので例を示します. 下図のような曲線の長さを求めることを考えます.

長さは,  から
から  までとして, 三角形の縦と横はそれぞれ
までとして, 三角形の縦と横はそれぞれ 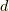
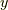 ,
, 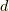
 とします.そして曲線の長さを
とします.そして曲線の長さを  とします.すると三平方の定理より
とします.すると三平方の定理より

両辺を 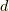
 で割ると
で割ると
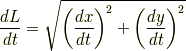
よって, =
=  とおいて
とおいて

と表すことができます.特に
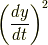
をよく 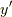 と表現されることを覚えておきましょう.曲線の長さ
と表現されることを覚えておきましょう.曲線の長さ  は関数
は関数 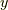 (グラフ)によって変化するものです.
(グラフ)によって変化するものです.
様々な変化がある中で  の最大・最小を考える手法が「変分法」と呼ばれる,数学的な技です.また,微分法との対応から
の最大・最小を考える手法が「変分法」と呼ばれる,数学的な技です.また,微分法との対応から  が停留値をとるとき
が停留値をとるとき 
 = 0 となります.
= 0 となります.
Important
汎関数  は最小値をとるものだと考えます.最小値をとった
は最小値をとるものだと考えます.最小値をとった  の変分
の変分 
 は
は 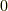 になります.
になります.
3.オイラーの方程式
上記の例から,  を(
を( 
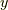
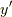 )の関数と考え,汎関数
)の関数と考え,汎関数  が次の形で表されると考えます.
が次の形で表されると考えます.
![L [y] = \int^b_a f(x,y,y')dx \tag{3.1}](http://hooktail.maxwell.jp/kagi/1c3ba865cb7a99cd41e91051642ec706.png)
ここで,下図のように終始の定点は固定し,経路を少しだけずらしたものを考えます.
青線を  [
[ 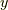 ],赤線を
],赤線を  [
[ 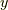 +
+ 
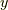 ]とおきます.
]とおきます. 
 =
=  [
[ 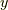 +
+ 
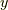 ] -
] -  [
[ 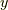 ]と表すことができるので,(3,1)を用いて
]と表すことができるので,(3,1)を用いて

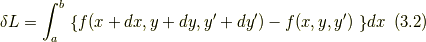
ここで,カッコの中身は微分方程式の形と考えることができるので,全微分してみます.
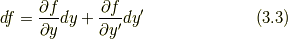
(3.2)と(3.3)より
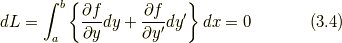
ここで,部分積分の公式を用いて
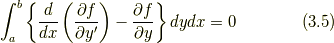
(3.5)の恒等式が成り立つためには,中括弧の中身が 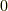 である必要があります.以上のことより
である必要があります.以上のことより
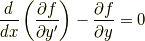
が成り立ちます.この式をオイラー方程式といいます.
見方によっては,オイラー方程式は位置を固定したバージョンのラグランジュ方程式と言うこともできます.
3.ラグランジュ方程式
さて,いよいよラグランジュ方程式の導出に入っていきます.最後は,上記のオイラー方程式を導く方法が必要になってきます.頑張っていきましょう.
余談ですが,今主流になっているラグランジュ方程式は,位置ではなく時間を固定した式になっています.イメージの話ですが,ある地点  から
から  まで物体を放ったとします.このとき,時間は
まで物体を放ったとします.このとき,時間は 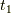 から
から 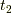 だけかかったとします.初期条件が決まっているとき,地点
だけかかったとします.初期条件が決まっているとき,地点  から
から  までは最小の距離を移動するようになっています.当たり前のように思う方がいるかもしれませんが,この考え方が重要になってきます.もしわかりにくいと言う方がいましたらこの余談は無視してください.
までは最小の距離を移動するようになっています.当たり前のように思う方がいるかもしれませんが,この考え方が重要になってきます.もしわかりにくいと言う方がいましたらこの余談は無視してください.
物体が静止しているとき,全体として力は,はたらいていないと考えることができます.また,様々な力がはたらいているもののそれらの力がつり合っている場合も考えることができます.このつり合いの状態を表すために,これらの力がはたらいている質点の位置  を仮想的に
を仮想的に 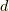
 だけ動かしてみることとします.すると,この時にされる仕事
だけ動かしてみることとします.すると,この時にされる仕事 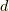
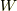 は(3.1)のように表すことができます.
は(3.1)のように表すことができます.
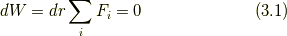
つまり,つり合いの状態では任意の微小な変位に対して仕事が 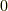 になると言うことができます.これを「仮想仕事の原理」といいます.仮想仕事の原理は便利な手法ではありますが,力のつり合いが成り立つ場合しか使うことができません.これを補うのが「ダランベールの原理」です.ダランベールの原理により,加速度運動している質点に対しても,仮想仕事の原理が適用できるようになるのです.
ここで,ニュートンの運動方程式を考えてみましょう.ニュートンの運動方程式は,(3.2)のような形をしています.
になると言うことができます.これを「仮想仕事の原理」といいます.仮想仕事の原理は便利な手法ではありますが,力のつり合いが成り立つ場合しか使うことができません.これを補うのが「ダランベールの原理」です.ダランベールの原理により,加速度運動している質点に対しても,仮想仕事の原理が適用できるようになるのです.
ここで,ニュートンの運動方程式を考えてみましょう.ニュートンの運動方程式は,(3.2)のような形をしています.

(3.2)は見方を変えれば(3.3)のようになりますね.
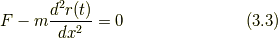
これは,見かけ上,力がつり合っているとみなすことができます.よって,仮想仕事の原理と同様の方法で(3.4)を導くことができます.
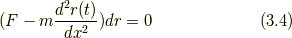
次に(3.1)の仮想仕事の原理を用いて,最初にハミルトンの変分原理(最小作用の原理のことです)を導きます.

この左辺と中辺の作用積分を積分区間[ 
 ]での時刻
]での時刻  による積分を
による積分を 
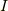 とおくと
とおくと
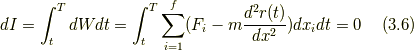
(3.6)式のようにできるのは,オイラー方程式を導く際に汎関数  が最小値をとる時,
が最小値をとる時, の変分
の変分 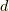
 は0にならないということが言えるからです(数学における変分原理を力学にも適用しようと試みたと考えることができます).(3.5)式のように仮想仕事の原理における式の形は
は0にならないということが言えるからです(数学における変分原理を力学にも適用しようと試みたと考えることができます).(3.5)式のように仮想仕事の原理における式の形は 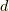
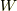 = 0となっており,変分が0であると考え,中辺を変形することで力学におけるオイラー方程式を導くことができます.
= 0となっており,変分が0であると考え,中辺を変形することで力学におけるオイラー方程式を導くことができます.
以下で(3.6)式の中辺を変形していきます.第1項と第2項をそれぞれ,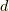
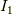 ,
, 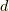
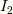 とおくと以下の式で表される.
とおくと以下の式で表される.

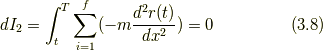
dI 1について
外力  が保存力であるとすると,ポテンシャル
が保存力であるとすると,ポテンシャル 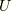 とおいて
とおいて
となります.これを(3.7)に代入して
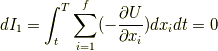
カッコの中はポテンシャル 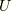 の全微分となっているので
の全微分となっているので
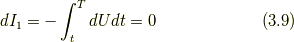
dI 2について
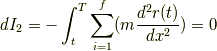
部分積分の公式を用いて
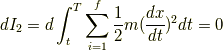
ここで,
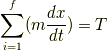
とおくと
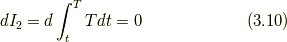

なので(3.9), (3.10)より
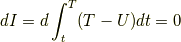
ここで

とおきます.
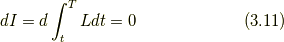
はい,ここまで長々と式変形をやってきました.結構大変でしたね.ここで出てきた  が力学における「ラグランジアン」と呼ばれるものです.(3.11)からはオイラー方程式を導く手順でラグランジュ方程式(3.12)を導くことができます.
が力学における「ラグランジアン」と呼ばれるものです.(3.11)からはオイラー方程式を導く手順でラグランジュ方程式(3.12)を導くことができます.
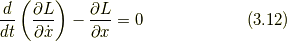
ちなみにラグランジアン  は,位置・速度・時間の関数で表されます.また,(3.11)はハミルトンの原理(最小作用の原理)と呼ばれています.
は,位置・速度・時間の関数で表されます.また,(3.11)はハミルトンの原理(最小作用の原理)と呼ばれています.
あとがき
以上,ラグランジュ方程式を導くところまでやってみました.解析力学の歴史を調べてみると,定式化に違いがあるみたいです.イメージとしては派閥みたいなものでしょうかね?今回追ってきたハミルトンの原理では, 位置を固定しているオイラー方程式とは違い, 時間を固定した方程式となっています.しかし, 歴史的には到達時間を固定しない形での定式化(モーペルチュイの最小原理)もされているみたいです.それでも
(1)ニュートンの運動方程式とすっきりとした対応関係があること
(2)有用な変分原理は時間を固定するものであること
以上2つの理由から, ハミルトンの原理が現在では使われています.私もあまり詳しくは調べていないので,興味のある方は調べてみてください.この考え方は, 力学だけでなく, 電磁気学や量子力学の分野でも用いられるものであります.力学分野ではラグランジュ方程式の導出過程から
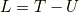
という関係式が導かれましたが, 電磁気学や量子力学,熱・統計力学,相対性理論など多岐にわたる分野で,ラグランジアンの関係式を見つけることで, さらに深い考察ができるようになります.解析力学って,数式ばかりであまり好きではありませんでしたが,こうして勉強してみると面白いですよ.時間があるときに,そちらの記事も書いてみようと思います.
今回は以上です.お疲れ様でした.