この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
グリーン関数を理解しよう(相互作用表示とS行列)
これからいくつかの記事を通して,
物性物理で扱われる絶対零度におけるグリーン関数の理解を目指します.
いくつかの定理などの証明は省略して,要点の俯瞰をする方針で行きます.
参考文献として,下に書くMahan先生の本を挙げて
おきます.このシリーズでは 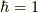 とします.
次の記事は 相関関数の計算 です.( 目次 )
とします.
次の記事は 相関関数の計算 です.( 目次 )
相互作用表示
まず,解が厳密には解けないハミルトニアンを 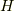 とします.
そして,非摂動ハミルトニアン(厳密に解ける)を
とします.
そして,非摂動ハミルトニアン(厳密に解ける)を 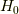 とします.
その差を
とします.
その差を 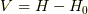 とします.ここで
とします.ここで  と書くと,
ポテンシャルを想像してしまうかと思いますが,
必ずしもポテンシャルではありません.
むしろ,(第二量子化演算子で表される)相互作用と言った方が適切です.
と書くと,
ポテンシャルを想像してしまうかと思いますが,
必ずしもポテンシャルではありません.
むしろ,(第二量子化演算子で表される)相互作用と言った方が適切です.
相互作用表示では演算子は 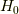 に従って時間発展します.
この表示の演算子をキャレット
に従って時間発展します.
この表示の演算子をキャレット  を付けて表します.
を付けて表します.
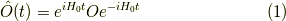
波動関数は以下の様な時間発展をします.
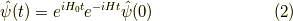
ここで, ![[H_0,V] \neq 0](http://hooktail.maxwell.jp/kagi/bdb6ce098b810beed48d17c7268d25fd.png) なので,
なので,
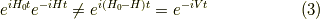
であることにご注意ください. 物理量の値の時間発展は,
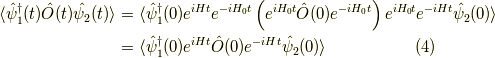
となり,シュレーディンガー表示やハイゼンベルク表示と同じであることが分かります.
さて,波動関数を時間微分してみましょう.

となります. ![[H_0, e^{iH_0t}] = 0, [H, e^{iHt}] = 0](http://hooktail.maxwell.jp/kagi/e54c4d5c81d9550ac320168d011e5d99.png) に気を付けて下さい.
よって,
に気を付けて下さい.
よって,
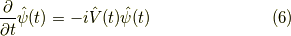
となります.
ここで 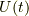 なる演算子を導入します.
なる演算子を導入します.

です.これは,波動関数の時間発展を表しますが,
EMANさんの記事の 時間発展演算子 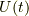 とは,
この記事の
とは,
この記事の 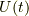 は相互作用表示を扱う点で異なります.
は相互作用表示を扱う点で異なります.
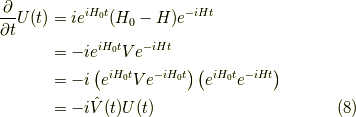
と言う,式 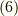 から時間依存性を抽出したような微分方程式を満たします.
ここで
から時間依存性を抽出したような微分方程式を満たします.
ここで 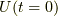 は全く時間が経っていない波動関数を返しますから,恒等演算子
は全く時間が経っていない波動関数を返しますから,恒等演算子 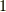 です.
です.
式 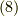 を
を 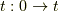 で積分すると,
で積分すると,
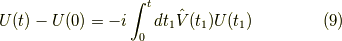
つまり,
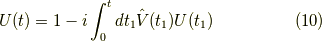
となります.ここで,右辺の 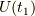 は左辺の
は左辺の 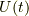 と同じ関数ですから,
と同じ関数ですから, 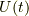 を
を 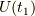 に代入することで,
逐次展開が出来て(この辺は発散とか考えない辺り物理学的ですね.結合定数が大きくこの級数が
に代入することで,
逐次展開が出来て(この辺は発散とか考えない辺り物理学的ですね.結合定数が大きくこの級数が  の増加と共に減りにくい時は扱いにくいという欠点があります.つまり,強い力等のことです.),
の増加と共に減りにくい時は扱いにくいという欠点があります.つまり,強い力等のことです.),
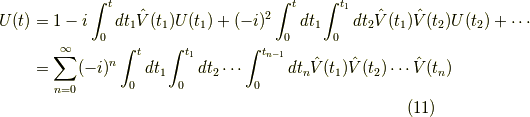
詳細は省きますが,時間順序演算子  なるものを使うと,この式は
なるものを使うと,この式は
![U(t) = T \exp \left[ -i \int_0^t dt_1 \hat{V}(t_1) \right] \tag{12}](http://hooktail.maxwell.jp/kagi/a97e43b2d1dc6ba3545f3ae8fe6d38e1.png)
と簡潔に表せます.時間順序演算子の意義はこの様に表記を簡潔に表せると言う事です. 決して,新しい計算方法で計算を簡単に出来るような代物ではありません. 簡潔な表記の裏には,泥臭い計算があるのです.
S行列
ここで,S行列なるものを考えます.行列とは言うものの演算子の仲間です. これも時間発展に関わります.
定義は,
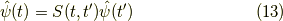
となる演算子です.ここで,

を使うと,
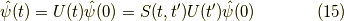
が言えるので,

と分かります.この演算子の性質を挙げていきます.
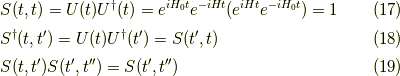
また,  での偏微分に対して,
での偏微分に対して, 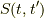 は
は 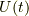 と同じ微分方程式を満たします.
と同じ微分方程式を満たします.
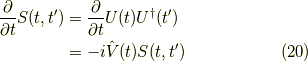
よって,
![S(t,t^\prime) &= U(t)U^\dagger(t^\prime) \\&= T \left( \exp \left[ -i \int_0^t dt_1 \hat{V}(t_1) \right] \exp \left[ i \int_0^{t^\prime} dt_1 \hat{V}(t_1) \right] \right) \\&= T \exp \left[ -i \int_{t^\prime}^t dt_1 \hat{V}(t_1) \right]\tag{21}](http://hooktail.maxwell.jp/kagi/133361a75c3f0edc90e8cc03b7924691.png)
と分かります.
ここで, 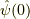 はシュレーディンガー表示の
はシュレーディンガー表示の 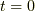 における波動関数
における波動関数 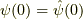 と同じです.
よって,
と同じです.
よって,

が言えます.今,絶対零度の振る舞いに興味があるので基底状態を知りたいです.
グリーン関数を決定するには 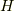 の厳密な基底状態の波動関数
の厳密な基底状態の波動関数 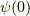 が必要です.
が必要です.
ここで,ゲルマン・ロウの定理というものがあります.(証明は書きません)
ハミルトニアンの解ける部分 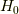 の基底状態を
の基底状態を 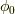 とすると,
その定理を使うことで,
とすると,
その定理を使うことで,
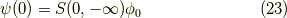
が言えます.一方,

より,
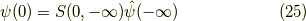
式 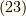 と比較することで,
と比較することで,

が分かります. 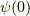 は
は  の存在下での正しい最低エネルギー固有状態になっています.
ちなみに
の存在下での正しい最低エネルギー固有状態になっています.
ちなみに
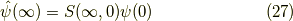
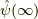 は
は 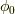 と位相因子
と位相因子 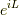 を通して関係します.
を通して関係します.

今日はこの辺りで一旦切りましょう.お疲れさまでした. 続きは 相関関数の計算 です.