この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。 リンクを正しく張れていないところが存在しますのでご注意ください。 正式公開まで、いましばらくお待ちください。
格子欠陥の統計力学とフェルミ分布

金属結晶を考えます．できるにはエネルギー 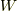W を必要とする，格子欠陥（格子以外の場所に割り込んだ同種の金属原子）を起こしている原子数を 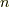n 個，格子を作っている原子数を 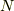N とすると，フェルミ分布関数から，

n = \dfrac{N}{e^{\beta W}+1} \tag{1}

と考えられます．この式を導出してみます．ただし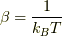， \beta = \dfrac{1}{k_B T} ，つまり逆温度です．

自由エネルギー

金属結晶は体積がほとんど変わらないので，膨張によるエネルギーは無視でき，ヘルムホルツの自由エネルギー 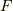F を考えれば良いでしょう．

F = E -TS \tag{2}
が基本です．ここで，格子欠陥ができる前のエネルギーを 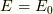E = E_0 とすると，
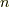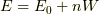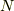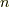n 個の欠陥ができた後は， E = E_0+ n W となります．また，およそ N 個の場所に n 個の欠陥原子が割り込んでいると，考えられますから，組み合わせの数は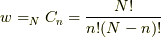， w=_NC_n=\dfrac{N!}{n!(N-n)!} となります．よって，エントロピーは，ボルツマンの関係式より，スターリングの公式 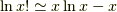\ln x! \simeq x \ln x - x を用いて，
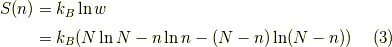
S(n) &= k_B \ln w \\&= k_B ( N \ln N - n \ln n -(N-n) \ln (N-n) ) \tag{3}

ですから，自由エネルギー 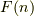F(n) は，

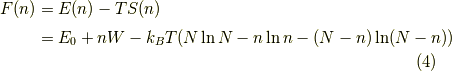
F(n) &= E(n) -TS(n) \\&= E_0 + n W - k_B T ( N \ln N - n \ln n -(N-n) \ln (N-n) ) \tag{4}

となります．さて，実現されるのは自由エネルギーが最小となる 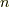n の値ですので，式 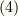(4) を微分してゼロに等しくなる 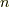n が実現される 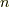n となります．

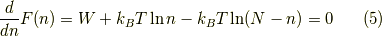
\dfrac{d}{d n} F(n) = W + k_B T \ln n - k_B T \ln (N-n) = 0 \tag{5}

よって，

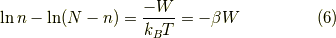
\ln n - \ln (N-n) = \dfrac{-W}{k_B T} = - \beta W \tag{6} \dfrac{n}{N-n} = e^{- \beta W} \tag{7} n = \dfrac{N}{e^{\beta W}+1} \tag{8}

が導けました．つまり，これはフェルミ分布した欠陥粒子数の期待値となります．これは，一つの欠陥サイトには一つしか原子が入れないと考えた為，フェルミオンの計算になったと考えられます．今日はこの辺で．お疲れ様でした．