この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
計量テンソルとヤコビアン
物の長さを測るには,物差しが必要です.数学的には『そもそも長さの概念は定義されてるの?』という部分も重要ですが,たとえ長さの概念が存在しても,それをどう測るかはまた別の話です.例えば長さの単位をどう決めるか,という問題があります.
一般に,座標系 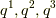 を決めると,この空間における曲線の微小な長さ
を決めると,この空間における曲線の微小な長さ 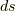 は,座標系
は,座標系 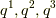 に沿った変化
に沿った変化 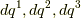 を使って表現できるはずです.
を使って表現できるはずです.
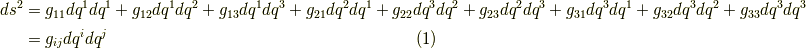
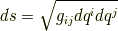
| [*] | よく見慣れているデカルト座標系では,微小長さ 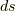 をピタゴラスの定理を使って をピタゴラスの定理を使って 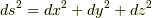 と表わせます.デカルト座標系には と表わせます.デカルト座標系には 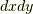 や や 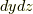 のような項は出てきませんが,これはよく考えてみれば,ピタゴラスの定理が成り立つ,という前提の上に物の長さを測っているということです. 球面三角形の角度 で少し触れましたが,曲率のある平面上に座標系を取る場合にはピタゴラスの定理がそのままでは成り立ちませんので,式 のような項は出てきませんが,これはよく考えてみれば,ピタゴラスの定理が成り立つ,という前提の上に物の長さを測っているということです. 球面三角形の角度 で少し触れましたが,曲率のある平面上に座標系を取る場合にはピタゴラスの定理がそのままでは成り立ちませんので,式 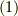 のような,より一般的な表式が必要です. のような,より一般的な表式が必要です. |
式 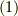 に出てくる
に出てくる  は 計量テンソル で,次のように定義されるのでした.
は 計量テンソル で,次のように定義されるのでした.
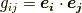
ここまでは既に勉強した内容ですが,忘れてしまった人は 計量テンソル を復習してください.
| [†] | 式 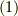 を満たす を満たす  で符号が正のものをリーマン計量と呼ぶことがあります.三次元ユークリッド空間内の曲面に距離の概念を付け足したものをリーマン空間と呼び,その曲面上での幾何学をリーマン幾何と呼びますが,そんな分野の用語です.現在の数学では,多様体や多様体上の点の接ベクトル等の概念から,リーマン空間やリーマン計量という言葉の意味はもう少し敷衍されていますが,基本的には曲面上で距離を測る話だと考えておいて間違いはありません.興味のある人は,リーマン幾何,微分幾何,多様体論などをキーワードに勉強してみてください.相対性理論にはミンコフスキー空間という,時間と空間を一緒にした四次元空間で出てきますが,ミンコフスキー空間に定義する計量は擬リーマン計量と呼ばれる,符号が負のものになります.違う空間に行けば『長さ』の概念も違うということですね. で符号が正のものをリーマン計量と呼ぶことがあります.三次元ユークリッド空間内の曲面に距離の概念を付け足したものをリーマン空間と呼び,その曲面上での幾何学をリーマン幾何と呼びますが,そんな分野の用語です.現在の数学では,多様体や多様体上の点の接ベクトル等の概念から,リーマン空間やリーマン計量という言葉の意味はもう少し敷衍されていますが,基本的には曲面上で距離を測る話だと考えておいて間違いはありません.興味のある人は,リーマン幾何,微分幾何,多様体論などをキーワードに勉強してみてください.相対性理論にはミンコフスキー空間という,時間と空間を一緒にした四次元空間で出てきますが,ミンコフスキー空間に定義する計量は擬リーマン計量と呼ばれる,符号が負のものになります.違う空間に行けば『長さ』の概念も違うということですね. |
微小面積と微小体積
また, 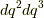 によって張られる微小面積は基底ベクトルの外積を使って次のように表現されます.デカルト座標系と違って微小面積は長方形にはならず,菱形で近似していることに注意してください.
によって張られる微小面積は基底ベクトルの外積を使って次のように表現されます.デカルト座標系と違って微小面積は長方形にはならず,菱形で近似していることに注意してください.
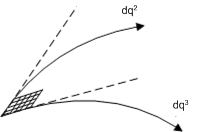
| [‡] | 曲線の微小部分を直線(図中の点線)で近似できるという考え方は積分計算の基本になっていました.これはよく考えるとそれほど自明ではないかも知れませんが,厳密な議論は解析学に譲ります.曲線の微小部分を直線で近似するという考え方自体は,読者の多くの方が微積分を習って以来,何度も目にしてきたと思いますし,ここではそのまま了解することにします.しかし,どんなに微小な長さを取っても,曲線の交わる角度を直角で近似することは出来ません.その結果,微小面積は上図のように菱形で表わされることになるわけです. |
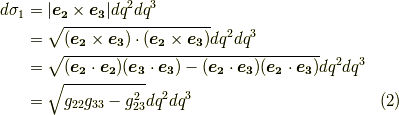
同様に,  や
や 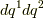 の張る微小面積は次のように表わせます.
の張る微小面積は次のように表わせます.

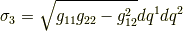
既に 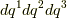 の張る微小体積
の張る微小体積 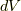 は 計量テンソル で勉強しました.忘れてしまった人は復習してみて下さい.
は 計量テンソル で勉強しました.忘れてしまった人は復習してみて下さい.

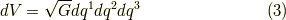
式 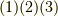 により,三次元の一般のアフィン座標系で,微小長さ
により,三次元の一般のアフィン座標系で,微小長さ 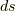 ,微小面積
,微小面積 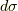 ,微小体積
,微小体積 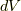 を表現することができました.式
を表現することができました.式 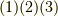 さえあれば,微積分をする準備はバッチリですね.
さえあれば,微積分をする準備はバッチリですね.
補足:直交座標系の場合
直交座標では  のうち
のうち  成分が全て零になりますから,大幅に式を簡単化することができます.(なぜ零になるのか忘れてしまった人は 直交座標系 を復習して下さい.)式
成分が全て零になりますから,大幅に式を簡単化することができます.(なぜ零になるのか忘れてしまった人は 直交座標系 を復習して下さい.)式 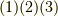 で,
で,  と置くと,式
と置くと,式 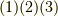 は次の式
は次の式 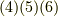 に帰着します.
に帰着します.
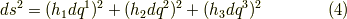



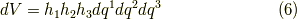
実際の計算では直交座標系を利用することが多いと思いますので,式  は重要です.
は重要です.
ヤコビアンとの関係
さきほど考えていた座標系 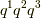 は,一般的な三次元のアフィン座標系だとします.この
は,一般的な三次元のアフィン座標系だとします.この 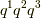 におけるベクトル成分を,一番便利な正規直交デカルト座標系
におけるベクトル成分を,一番便利な正規直交デカルト座標系 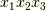 で表現し直してみましょう.
で表現し直してみましょう. 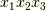 も独立な三次元の座標系ですから,各
も独立な三次元の座標系ですから,各  を
を 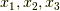 と関係づけることが可能なはずです.そこで,各
と関係づけることが可能なはずです.そこで,各  を
を 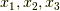 の関数だと考えます.
の関数だと考えます.



このとき,ヤコビ行列  は次のように定義されます.
は次のように定義されます.
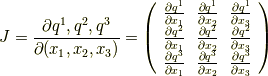
ヤコビアン 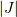 はヤコビ行列の行列式として次のように書けます.
はヤコビ行列の行列式として次のように書けます.
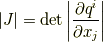
| [§] | ヤコビ行列そのものをヤコビアンと呼ぶ人もいれば,行列式の方をヤコビアンと呼ぶ人もいます.どうも用語が混乱しているようです.混乱を避けるため,この記事では  と と 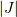 という記号を使い分けることにしました.海外の教科書でも用語は統一されていないようなので,注意してください. という記号を使い分けることにしました.海外の教科書でも用語は統一されていないようなので,注意してください. |
逆に, 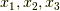 を
を 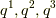 の関数として表わすことも出来るはずです.
の関数として表わすことも出来るはずです.



式 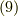 より,ヤコビアン
より,ヤコビアン 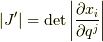 を考えることが出来ますが,このヤコビ行列は先ほどの
を考えることが出来ますが,このヤコビ行列は先ほどの  のちょうど逆行列になっています.
のちょうど逆行列になっています.
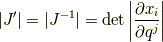
| [¶] |  から から 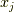 , , 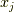 から から  と変数変換を二回繰り返せば元に戻りますから,この二つのヤコビアンが互いに逆行列の関係になっていることは当然だと言えます.偏導関数に関して と変数変換を二回繰り返せば元に戻りますから,この二つのヤコビアンが互いに逆行列の関係になっていることは当然だと言えます.偏導関数に関して  が成り立つことからも確認できます.また, が成り立つことからも確認できます.また,  と と 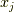 はどちらも独立な基底の組であることを前提にしていますが,このことは式 はどちらも独立な基底の組であることを前提にしていますが,このことは式  のような表現が可能であることと同値であると言えます.つまり変数の一意的な変換には必ず逆変換が存在し,このときヤコビアンは正則な行列(逆行列がある)になるはずなのです. のような表現が可能であることと同値であると言えます.つまり変数の一意的な変換には必ず逆変換が存在し,このときヤコビアンは正則な行列(逆行列がある)になるはずなのです. |
ヤコビアンは座標変換に関係する量ですから,いかにも計量テンソルと関係がありそうだという気がします.計量テンソルを考えるために,まず微小長さ 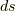 をベクトル表記で
をベクトル表記で 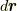 と表わしてみましょう.
と表わしてみましょう.
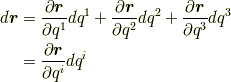
これより,次式が成り立ちます.

一方,式 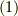 より
より 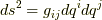 ですから,式
ですから,式 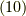 と比べて次式が言えます.
と比べて次式が言えます.
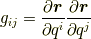
ここで 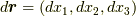 を代入すれば,次のように書き換えることができます.
を代入すれば,次のように書き換えることができます.

蛇足ですが,定義より計量テンソルは 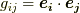 であって,式
であって,式 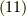 と見比べて次の関係式も言えます.
と見比べて次の関係式も言えます.
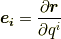

さて,ヤコビアン ![J'= \left[ \frac{\partial x_{i}}{\partial q^{j}} \right]](http://hooktail.maxwell.jp/kagi/91e8b5b4da90d63a8a2299eb48c345e9.png) と計量テンソル
と計量テンソル  を比べてみましょう.どちらも
を比べてみましょう.どちらも 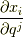 の形の項から成り立っており,明らかに仲間という感じがしますが,そのまま同一というわけではありません.計量テンソルは二つの偏微分の積の形になっていますが,ヤコビアンを二つ掛け合わせて計量テンソルを表わせないでしょうか.
の形の項から成り立っており,明らかに仲間という感じがしますが,そのまま同一というわけではありません.計量テンソルは二つの偏微分の積の形になっていますが,ヤコビアンを二つ掛け合わせて計量テンソルを表わせないでしょうか.
少し考えてみると,次の関係式が分かると思います.  は
は 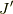 の転置行列の意味とし,
の転置行列の意味とし,  を成分とする行列を
を成分とする行列を ![[g_{ij}]](http://hooktail.maxwell.jp/kagi/d581215a94277a312354bf461cea928e.png) と書いています.
と書いています.
![[g_{ij}] &= {}^{t}{J'} J' \\ &= \left( \begin{array}{ccc}\frac{\partial x^1}{\partial q_{1}} & \frac{\partial x^2}{\partial q_{1}} & \frac{\partial x^3}{\partial q_{1}} \\\frac{\partial x^1}{\partial q_{2}} & \frac{\partial x^2}{\partial q_{2}} & \frac{\partial x^3}{\partial q_{2}} \\\frac{\partial x^1}{\partial q_{3}} & \frac{\partial x^2}{\partial q_{3}} & \frac{\partial x^3}{\partial q_{3}} \\ \end{array} \right) \left( \begin{array}{ccc}\frac{\partial x^1}{\partial q_{1}} & \frac{\partial x^1}{\partial q_{2}} & \frac{\partial x^1}{\partial q_{3}} \\\frac{\partial x^2}{\partial q_{1}} & \frac{\partial x^2}{\partial q_{2}} & \frac{\partial x^2}{\partial q_{3}} \\\frac{\partial x^3}{\partial q_{1}} & \frac{\partial x^3}{\partial q_{2}} & \frac{\partial x^3}{\partial q_{3}} \\ \end{array} \right) \\&=\left( \begin{array}{ccc}\left( \frac{\partial x^1}{\partial q_{1}} \right)^2 + \left( \frac{\partial x^2}{\partial q_{1}} \right)^2 +\left( \frac{\partial x^3}{\partial q_{1}} \right)^2 &\frac{\partial x^1}{\partial q_{1}}\frac{\partial x^1}{\partial q_{2}} + \frac{\partial x^2}{\partial q_{1}}\frac{\partial x^2}{\partial q_{2}} + \frac{\partial x^3}{\partial q_{1}}\frac{\partial x^3}{\partial q_{2}} & \frac{\partial x^1}{\partial q_{1}}\frac{\partial x^1}{\partial q_{3}} + \frac{\partial x^2}{\partial q_{1}}\frac{\partial x^2}{\partial q_{3}} + \frac{\partial x^3}{\partial q_{1}}\frac{\partial x^3}{\partial q_{3}} \\ \frac{\partial x^1}{\partial q_{2}}\frac{\partial x^1}{\partial q_{1}} + \frac{\partial x^2}{\partial q_{2}}\frac{\partial x^2}{\partial q_{1}} + \frac{\partial x^3}{\partial q_{2}}\frac{\partial x^3}{\partial q_{1}} & \left( \frac{\partial x^1}{\partial q_{2}} \right)^2 + \left( \frac{\partial x^2}{\partial q_{2}} \right)^2 +\left( \frac{\partial x^3}{\partial q_{3}} \right)^2 &\frac{\partial x^1}{\partial q_{2}}\frac{\partial x^1}{\partial q_{3}} + \frac{\partial x^2}{\partial q_{2}}\frac{\partial x^2}{\partial q_{3}} + \frac{\partial x^3}{\partial q_{2}}\frac{\partial x^3}{\partial q_{3}} \\ \frac{\partial x^1}{\partial q_{3}}\frac{\partial x^1}{\partial q_{1}} + \frac{\partial x^2}{\partial q_{3}}\frac{\partial x^2}{\partial q_{1}} + \frac{\partial x^3}{\partial q_{3}}\frac{\partial x^3}{\partial q_{1}} & \frac{\partial x^1}{\partial q_{3}}\frac{\partial x^1}{\partial q_{2}} + \frac{\partial x^2}{\partial q_{3}}\frac{\partial x^2}{\partial q_{2}} + \frac{\partial x^3}{\partial q_{3}}\frac{\partial x^3}{\partial q_{2}} & \left( \frac{\partial x^1}{\partial q_{3}} \right)^2 + \left( \frac{\partial x^2}{\partial q_{3}} \right)^2 +\left( \frac{\partial x^3}{\partial q_{3}} \right)^2 \\ \end{array} \right) \tag{11}](http://hooktail.maxwell.jp/kagi/e9018e32195f1e28c0a8a3e409247eb0.png)
右辺の係数を縮約を使ってまとめると,一般に次のように書けるでしょう.  は行列
は行列  の
の 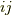 成分という意味です.
成分という意味です.

式 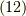 と式
と式 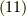 が等しいことを確認してください.
が等しいことを確認してください.