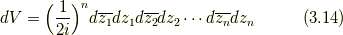この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
三次元対象物の複素積分表現(事例紹介)
本記事では, 複素解析の教科書ではあまり見られない,三次元対象物の複素積分による表現をいくつかの事例で紹介します. 従来と少し異なる視点を提供することにより, 複素解析を学ばれる方々の刺激になることを期待しています.
1. 基本的な式
ここでは, コーシーの積分公式を含む複素解析の基本的な式を取り上げる. 詳しい定義や導出等は複素解析の教科書をご参照願いたい.
さて, 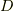 は複素平面上の単連結領域(穴が開いていない領域)とし,
は複素平面上の単連結領域(穴が開いていない領域)とし, 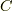 はそれを囲うある長さを持つ単純閉曲線(自身と交わらない閉じた曲線)とする.
はそれを囲うある長さを持つ単純閉曲線(自身と交わらない閉じた曲線)とする. 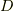 の任意の一点
の任意の一点  において, 以下のコーシー・ポンペイウの公式(Cauchy-Pompeiu Formula)が成り立つ.
において, 以下のコーシー・ポンペイウの公式(Cauchy-Pompeiu Formula)が成り立つ.
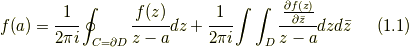
ここで,  は, 複素数
は, 複素数  の複素共役(complex conjugate)である. また,
の複素共役(complex conjugate)である. また,

であることから, 式(1.1)は二項目を書き変えて,
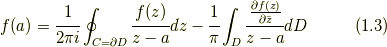
とも表せる.
さて, 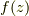 が
が 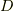 上の正則関数(holomorphic function)であるとき,
上の正則関数(holomorphic function)であるとき,  であるので, 式(1.1)あるいは式(1.3)は,
であるので, 式(1.1)あるいは式(1.3)は,
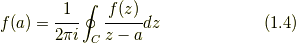
となる. これがコーシーの積分公式(Cauchy Integral Formula)と呼ばれるものである. また, 式(1.4)の特別な場合 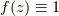 として, いわゆるコーシーの積分定理(Cauchy Integral Theorem)が成り立つ.
として, いわゆるコーシーの積分定理(Cauchy Integral Theorem)が成り立つ.
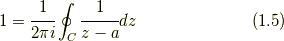
そして, 式(1.4)と式(1.5)から次が成り立つ.
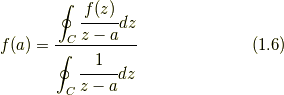
なお, 式(1.1)において, 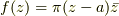 (これは正則関数ではない)とおけば,
(これは正則関数ではない)とおけば,

という  に関する基本的な関係式が得られる.
に関する基本的な関係式が得られる.
2. コーシーの積分公式の幾何学的解釈
三次元対象物の複素積分による表現に入る前に, 複素積分自体の幾何学的意味を見るために, ある変数変換により式(1.6)を書き換え, コーシーの積分公式の幾何学的な解釈を行ってみよう.
2.1 変数変換
以下の変数変換を考える.

ここで, 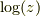 は自然対数である. 複素関数の対数は一般に多価性があるが, 本稿では1価に制限されているものとする.
は自然対数である. 複素関数の対数は一般に多価性があるが, 本稿では1価に制限されているものとする.
ここで,  ,
,  とすると, この変数変換に伴い
とすると, この変数変換に伴い 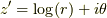 ,
, 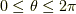 になり, 単純閉曲線
になり, 単純閉曲線 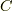 は, 開いた曲線
は, 開いた曲線  になる.
になる.
2.2 幾何学的解釈
式(1.6)は, 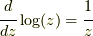 及び変数変換(2.1)を用いると, 以下のように書き換えられる.
及び変数変換(2.1)を用いると, 以下のように書き換えられる.
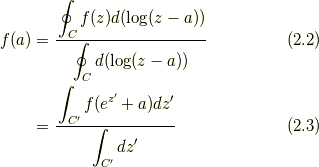
式(2.3)によれば, 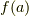 は, (開いた)曲線
は, (開いた)曲線  に沿って
に沿って 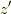 が動いた時の関数
が動いた時の関数 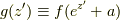 の平均値(あるいは重心)を与えていると解釈できる. それゆえ, 式(2.3)は, 平均値の定理(mean-value theorem)と呼ばれる.
の平均値(あるいは重心)を与えていると解釈できる. それゆえ, 式(2.3)は, 平均値の定理(mean-value theorem)と呼ばれる.
2.3 解釈の整合性
実は, 上記の議論で,
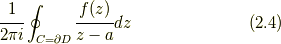
という積分は, 変数変換(2.1)を行わなくてもそのまま, 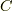 上を
上を 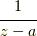 という関数について
という関数について  で積分するとき,
で積分するとき, 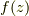 という重みを与えて平均化している, とも解釈でき, しかもこの解釈自体は
という重みを与えて平均化している, とも解釈でき, しかもこの解釈自体は 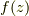 が正則か否かには関係ない. そのため, たとえば, 式(1.1)の右辺第一項にもこの解釈を適用可能である.
が正則か否かには関係ない. そのため, たとえば, 式(1.1)の右辺第一項にもこの解釈を適用可能である.
さて, 平均値(2.4)は, 平均値(2.4)自体を関数 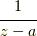 で
で 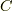 にそって
にそって  で積分する合計値と一致するはずである. すなわち,
で積分する合計値と一致するはずである. すなわち,
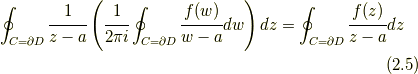
実際, ここで, 左辺の括弧内に式(1.1)を用いれば,
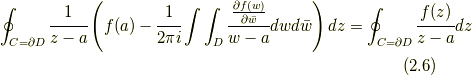
であり, 左辺は,
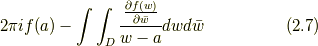
であることから, 両辺を 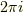 で割れば, コーシー・ポンペイウの公式が再現され, この公式と整合していることが確認される.
で割れば, コーシー・ポンペイウの公式が再現され, この公式と整合していることが確認される.
3. 三次元的な対象物を複素積分で表現する
筆者は, 中学の終わりごろから, 独学で微分積分学を学び, ついでベクトル解析を学び,  次元球などの一般次元の空間の対象物を取り扱えるようになったあとで, 複素解析を学び始めた途端, 空間が突如二次元の世界に限定されてしまったような印象を持った. たとえば, せっかく習得したストークスの定理(Stokes' Theorem)などはどこへ行ってしまったのか, と思ったりした.
次元球などの一般次元の空間の対象物を取り扱えるようになったあとで, 複素解析を学び始めた途端, 空間が突如二次元の世界に限定されてしまったような印象を持った. たとえば, せっかく習得したストークスの定理(Stokes' Theorem)などはどこへ行ってしまったのか, と思ったりした.
しかし, もちろん, 複素解析には本来そのような限定はない. 三次元以上の空間の対象と結び付けることが可能である. ここでは, 簡単な事例を挙げてそのことを示したい.
3.1 立体の体積
式(1.2)(または, 式(1.7))から,
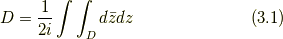
である. ここで, 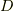 が時間的に変化する(つまり
が時間的に変化する(つまり 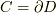 が時間的に変化する)としよう. すなわち, 各時点
が時間的に変化する)としよう. すなわち, 各時点  での複素平面というものを考えることにする.
での複素平面というものを考えることにする.

立体の体積を複素積分で表現するために, 立体を一方向に平面でスライスしていく. このとき各平面が各時点の複素平面であるようにする. すると, 時刻 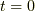 から 時刻
から 時刻 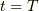 までかけて
までかけて 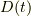 は点から立体の断面になり, 立体の体積
は点から立体の断面になり, 立体の体積  は, 以下のように表せる.
は, 以下のように表せる.
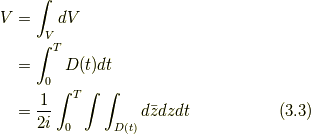
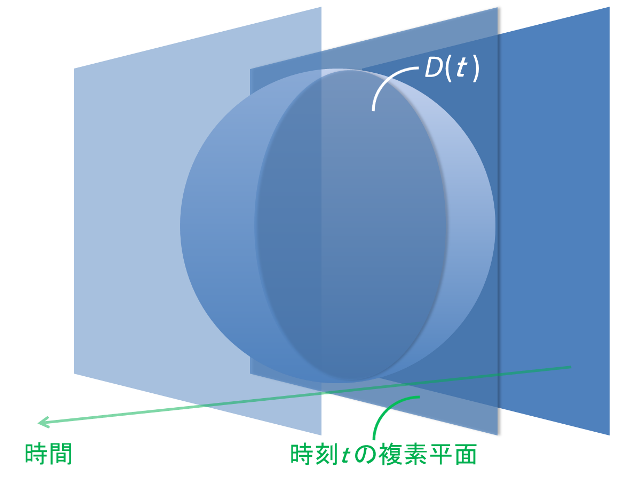
3.2 球の体積
ここで, 具体的な例として, 3次元の球を対象に考えてみよう. 球をある直径に沿って刻々とスライスしていく断面  を考える.時刻
を考える.時刻  から 時刻
から 時刻 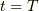 までかけて
までかけて 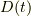 は点から半径
は点から半径 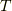 の円盤になり, 時刻
の円盤になり, 時刻 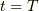 から 時刻
から 時刻 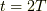 までかけて
までかけて 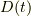 は再び点になるとする. 時刻
は再び点になるとする. 時刻  のときの
のときの 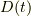 は,
は,
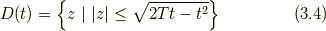
となり, 時刻 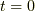 から 時刻
から 時刻 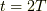 まで厚み
まで厚み 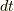 の円盤
の円盤 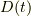 を積分する形で球の体積が求まり,
を積分する形で球の体積が求まり,
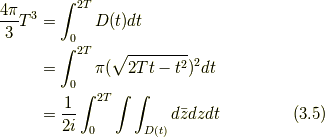
- という関係が得られる.
ところで, 式(3.5)では, 時刻  の円盤(つまり2次元球)
の円盤(つまり2次元球) 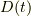 を足し上げて三次元球の体積を求めたわけだが, 同様にして三次元球を足し上げることで, 四次元球の体積を求めることができる. 時刻
を足し上げて三次元球の体積を求めたわけだが, 同様にして三次元球を足し上げることで, 四次元球の体積を求めることができる. 時刻  のときの三次元球の体積
のときの三次元球の体積 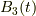 は,
は,
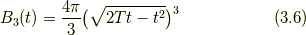
であり, 四次元球の体積は,
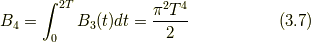
となる. このことを踏まえ, 時刻をもう一つ増やして, 式(3.5)に類似した形で 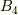 について複素積分で表すと,
について複素積分で表すと,
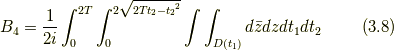
となる. このようにして, 複素積分を一般次元の球の体積と結び付けられる. なお, ここで,  である.
である.
3.3 ストークスの定理
3.1項と同様に, 各時点の複素平面を考えることで三次元的な空間を作る. 座標としては, 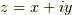 と
と  を使って, 位置ベクトル
を使って, 位置ベクトル 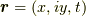 を考える. すると, 線素は
を考える. すると, 線素は 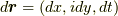 , 面積要素は
, 面積要素は 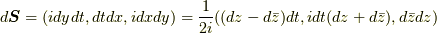 になる. ただし, ここで,
になる. ただし, ここで, 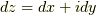 ,
, 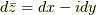 である.
である.
このような複素数を含んだベクトル表示における二つのベクトル 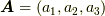 ,
, 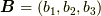 の内積及び外積を次のように定義することとする.
の内積及び外積を次のように定義することとする.
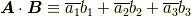

これらはそれぞれ成分が実数の場合の定義を包含している. なお,このとき,ベクトル 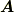 の大きさ(ノルム)は, 成分が実数の場合と同様に
の大きさ(ノルム)は, 成分が実数の場合と同様に  で与えられる.
で与えられる.
さて, ベクトル場 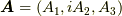 に対し, 同三次元空間の単純閉曲線
に対し, 同三次元空間の単純閉曲線  とそれを縁とする曲面
とそれを縁とする曲面 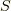 について,
について,

であり, 実数解析のストークスの定理を利用することで, そのままストークスの定理(Stokes' Theorem)が成り立つ.
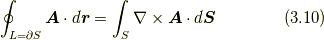
ただし, ここで,  である.
である.
ガウスの定理(Gauss' Theorem)については,三次元空間のベクトル場 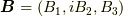 を考えれば, 同三次元空間の単純閉曲面
を考えれば, 同三次元空間の単純閉曲面 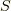 とそれを縁とする体積
とそれを縁とする体積  について,
について,

であり, 実数解析のガウスの定理を利用することで, そのままガウスの定理が成り立つ.
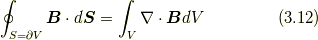
同様にして, ベクトル解析の諸公式を複素積分で表現することができる. ここでは詳しく展開できないが, 当然のことながら, 三次元の流体力学等を複素積分で表現することも可能である.
3.4 パップスの定理
3.3項で導入した 位置ベクトル  , 線素
, 線素 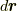 及び面積要素
及び面積要素 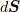 の表式を用いれば, 幾何学のパップス・ギュルダンの定理(Pappus-Guldinus theorem)(以下, パップスの定理)を複素積分で表現できる.
の表式を用いれば, 幾何学のパップス・ギュルダンの定理(Pappus-Guldinus theorem)(以下, パップスの定理)を複素積分で表現できる.
パップスの定理では, 断面上のすべての点が断面に垂直になるように(すなわち 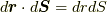 となるように)断面
となるように)断面 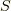 を動かし, それが掃する体積
を動かし, それが掃する体積  が
が 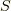 の重心の動いた道のり
の重心の動いた道のり  と面積
と面積 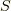 の積になる. 3.2項では, 直線方向に時点の異なる複素平面が並んだが, この並び方は回転してもいい. このようなことを利用して, たとえば, 半円盤を直径の周りに回転させて球を作り, その体積から半円盤の重心の位置を求めたり, これを高次化して, 半球を直径断面の周りに回転させて四次元球を作り, その体積から半球の重心の位置を求めたりすることができる. 重心の軌道のパラメータを
の積になる. 3.2項では, 直線方向に時点の異なる複素平面が並んだが, この並び方は回転してもいい. このようなことを利用して, たとえば, 半円盤を直径の周りに回転させて球を作り, その体積から半円盤の重心の位置を求めたり, これを高次化して, 半球を直径断面の周りに回転させて四次元球を作り, その体積から半球の重心の位置を求めたりすることができる. 重心の軌道のパラメータを 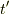 とすると, パップスの定理は一般式としては,
とすると, パップスの定理は一般式としては,
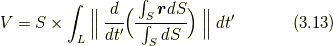
と表すことができる. ただし, 上で,  ,
, 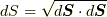 である.
(パップスの定理について, 詳しくは本記事末の関連メモをご覧いただきたい.)
である.
(パップスの定理について, 詳しくは本記事末の関連メモをご覧いただきたい.)
3.5 補足
多変数複素解析では, 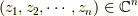 を用いて,
を用いて,  次元の空間
次元の空間 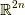 内の体積を扱うことができる.
内の体積を扱うことができる.