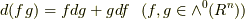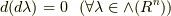この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
微分形式の張る空間と座標変換
この記事の内容は,今まで勉強してきた内容の,代数的なおさらいです.多少,言い忘れた事柄も補足しますが,特に目新しい話はありませんので,もし何か引っかかる部分があれば,今のうちに復習しておいて下さい.
微分形式の張る空間
ベクトル空間 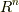 上で定義される微分形式の全体
上で定義される微分形式の全体  は,
は,  次以下の外積空間の直和として,次のように書けるでしょう.
次以下の外積空間の直和として,次のように書けるでしょう.
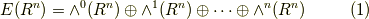
ここで 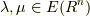 とすると,
とすると,  と
と 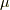 の間には
の間には  内で次のような結合を考えることが出来ます.
内で次のような結合を考えることが出来ます.
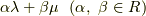
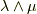
 (
( 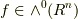 は関数)
は関数)
一番目の線形結合は,  と
と 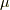 が同じ次数の微分形式でなければ意味がありません.(次数の異なる微分形式に,和は定義できません.)また,これらの演算とは別に
が同じ次数の微分形式でなければ意味がありません.(次数の異なる微分形式に,和は定義できません.)また,これらの演算とは別に  には外微分と呼ばれる写像
には外微分と呼ばれる写像 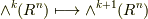 が定義されていました.外微分には,次のような性質がありました.詳しくは, 外微分 , ポアンカレの補題 , 外微分の座標不変性 を復習してください.
が定義されていました.外微分には,次のような性質がありました.詳しくは, 外微分 , ポアンカレの補題 , 外微分の座標不変性 を復習してください.
| [*] | 外積代数の記号である 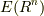 や や 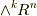 を使って微分形式の張るベクトル空間を表現しましたが,外積代数そのものには,外微分は定義されていなくても良く,微分形式には外微分が必須ですので,微分形式の張る空間には,『外微分が入った構造だよ』ということを明示的に示すために何か他の記号を使った方が良かったかも知れません.一般に,積や和といった代数構造と,微分や積分といった操作は別なのです.あまり色々出て来ると面倒なので,横着しました. を使って微分形式の張るベクトル空間を表現しましたが,外積代数そのものには,外微分は定義されていなくても良く,微分形式には外微分が必須ですので,微分形式の張る空間には,『外微分が入った構造だよ』ということを明示的に示すために何か他の記号を使った方が良かったかも知れません.一般に,積や和といった代数構造と,微分や積分といった操作は別なのです.あまり色々出て来ると面倒なので,横着しました. |
微分形式の座標変換
このセクションでは,微分形式の座標変換を考えてみます.すでに,関数 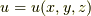 等の 全微分として知っていた公式は,一次微分形式の座標変換の式だと読むこともできます.
等の 全微分として知っていた公式は,一次微分形式の座標変換の式だと読むこともできます.
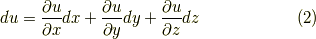
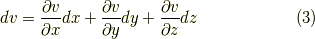
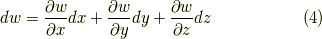
式  をあわせれば,
をあわせれば, 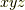 座標系から
座標系から  座標系への座標変換が表わされていることが分かると思います.二次微分形式の基底は次のように変換されます.ヤコビアンがたくさん出てきます.( 面積素と微分形式 も参考にしてみて下さい.)
座標系への座標変換が表わされていることが分かると思います.二次微分形式の基底は次のように変換されます.ヤコビアンがたくさん出てきます.( 面積素と微分形式 も参考にしてみて下さい.)
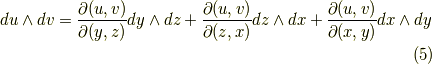
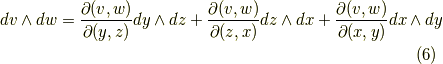
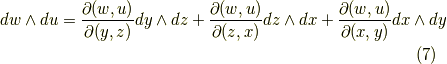
三次微分形式の変換は(一次元なので)もっと単純で,次のようになります.
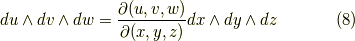
ヤコビアンの符号は,空間の向きを保つ変換の場合には正,向きを逆にする変換の場合には負になる点にも注意して下さい.これらの変換公式の意味は,重積分の際の積分変数の変換公式 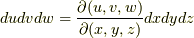 等の拡張になっています.
等の拡張になっています.
Important
微分形式の座標変換は,重積分の積分変数の変換公式のパワーアップ版です.
何度も強調しているように『積分の向き』『面積分の向き』『座標系が右手系か左手系か』といった情報を織り込めるという点で,ただの重積分の変数変換よりも,微分形式は多くの情報を含んでいます.これは,変数変換のヤコビアンの性質が,うまく組み込まれているからです.
| [†] | 積分計算と変数変換の論理を一貫させたために,形式的に『負の面積』『負の体積』といった量が出てきました.これらに物理的な応用を見つけることは出来ますが,原始的な直観としては,負の体積などは受け容れがたい概念でしょう.論理を美しく簡潔に整理していくと,原始的な直観だけでは太刀打ちできなくなってきます.それを,視野がより広がったと見るか,論理の整合性のための犠牲と見るかは,受け手の感情によるのでしょう. |
ヤコビアン
以前, 面積素と微分形式 で説明したように,ウェッジ積の性質(交代性)は,ヤコビアンの性質(行や列を入れ替えると符号が変わる)と見事に一致するため,重積分の積分変数を微分形式で表わすと,曲面の向きや空間の向きを保つのに非常に都合が良いことを見ました.これは復習事項です.
もう一つ,微分形式と変数変換について,変数変換に際して,変数の次数が変わっても構わないという点に注意して下さい.次元が変わる場合の変換の公式は次式のようになります.
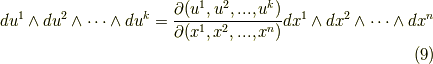
ここでヤコビアン 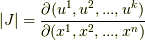 は,
は, 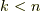 ならば横長の,
ならば横長の, 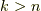 ならば縦長の行列式になります.いずれにせよ,ヤコビ行列の各成分
ならば縦長の行列式になります.いずれにせよ,ヤコビ行列の各成分 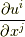 が非零な滑らかな関数であることが条件で,この場合,ヤコビアンの次数は縮退しません.つまり
が非零な滑らかな関数であることが条件で,この場合,ヤコビアンの次数は縮退しません.つまり 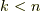 ならば
ならば 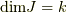 ,
, 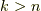 ならば
ならば  が要請されます.(これは線形代数の問題なので,ここでは証明はしません.)
が要請されます.(これは線形代数の問題なので,ここでは証明はしません.)
| [‡] | 外積代数は交代形式のテンソル解析だと見ることが出来ましたので,微分形式の理論もテンソル解析の一分野に過ぎない,という考えの人もいるかも知れません.しかし,古典的なテンソル解析では,変数の変換で次数が変わることはあまりありませんでしたので,この点に関しては微分形式の方がずっと自由だと言えます(むしろ古典的なテンソル解析で主に考えたのは,直交変換という,非常に特殊な変換でした.).変数の次数が減る,というのは,例えば射影のように,ふくらみのある立体をつぶしてしまう,というような場合(射影)が当てはまります.逆に,変数の次数を増やすというのは,つぶれた図形を膨らませるような変数変換だということです.特に,膨らますという操作には少し違和感を覚えるかも知れませんが, 微分形式の引き戻し という操作で,この話を重点的に考えます.こんな話題があったことを,頭の片隅に引っ掛けておいて下さい. |
テンソルとしてみた場合の微分形式
このセクションでは,テンソル解析の手法に戻って,久しぶりに添字を使った表記を考えてみたいと思います.ウェッジ積は交代形式のテンソル積だと考えることが出来ますから(そして外積代数は交代形式のテンソル代数),微分形式をテンソルとして表現することも出来るわけです.実際,昔風の教科書の中には,微分形式の理論をテンソル解析の一分野として扱っているものもあります.今さら,テンソルの添字計算に戻るメリットはあまりありませんが,テンソル解析との関係をすっきり理解しておくことは有意義でしょう.ウェッジ積 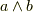 は,テンソル積を使えば次のように書くことが出来ます.
は,テンソル積を使えば次のように書くことが出来ます.
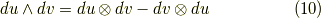
成分表記すれば, 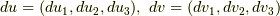 として,式
として,式 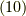 右辺のテンソル積は次のように表わせます.
右辺のテンソル積は次のように表わせます.
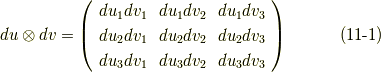
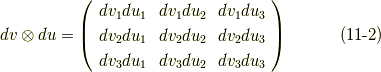
式  より,次式が言えます.
より,次式が言えます.
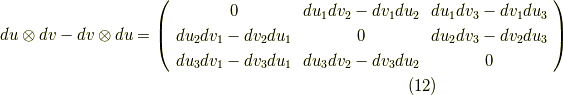
これは反対称行列で,これを行列 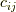 と名づければ,成分の添字表記で
と名づければ,成分の添字表記で ![c_{ij}=[du_{i}dv_{j}-dv_{i}du_{j}]](http://hooktail.maxwell.jp/kagi/3604183b5548f89c56e5e2b274e14a06.png) のように簡単に書けるでしょう.ウェッジ積
のように簡単に書けるでしょう.ウェッジ積 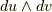 はこのような行列と同じだと考えても良いということになります.(ウェッジ積の交代性
はこのような行列と同じだと考えても良いということになります.(ウェッジ積の交代性 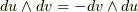 が確かに満たされることを確認して下さい.)
が確かに満たされることを確認して下さい.)  の反対称行列は実質的に三成分なので,三次元ベクトルと同型だと見ることが出来ました.
の反対称行列は実質的に三成分なので,三次元ベクトルと同型だと見ることが出来ました.
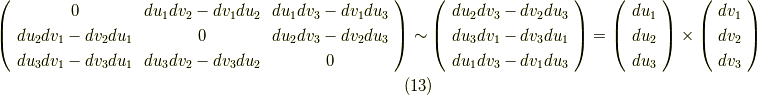
式 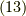 の右辺の絶対値は,ベクトルの外積の定義より,ベクトル
の右辺の絶対値は,ベクトルの外積の定義より,ベクトル 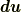 と
と 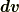 の張る微小な平行四辺形になります.ベクトル形で見れば,
の張る微小な平行四辺形になります.ベクトル形で見れば, 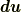 から
から 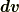 へ反時計回りに回るときに間に来る面積を正とする向きつき面積と見ることが出来ますから,これをそのままウェッジ積
へ反時計回りに回るときに間に来る面積を正とする向きつき面積と見ることが出来ますから,これをそのままウェッジ積 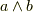 の幾何学的意味として採用すれば,意味が分かりやすいでしょう.
の幾何学的意味として採用すれば,意味が分かりやすいでしょう.
| [§] | 式 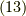 で,反対称行列とベクトルを対応させた同型写像 で,反対称行列とベクトルを対応させた同型写像 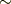 にはある程度の任意性があります.たとえば,中辺のベクトルに にはある程度の任意性があります.たとえば,中辺のベクトルに 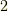 を掛けた形の同型写像も作れます.この場合, を掛けた形の同型写像も作れます.この場合, 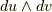 は『 は『 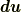 と と 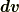 の張る微小な平行四辺形の向きつき面積の の張る微小な平行四辺形の向きつき面積の 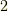 倍』と定義されるわけです.そんな定義は素直ではないので,採用しないだけです.それにしても, 面積素と微分形式 では,単にウェッジ積の性質と向きつき面積の性質(つまりはヤコビアンの性質)を比べて,ウェッジ積は向きつき面積だと考えることが出来る,と(代数的な性質だけから)決めてしまいましたが,上述のようにテンソルとして見ることで,もう少しこのような見方の根拠が明確になったと思います. 倍』と定義されるわけです.そんな定義は素直ではないので,採用しないだけです.それにしても, 面積素と微分形式 では,単にウェッジ積の性質と向きつき面積の性質(つまりはヤコビアンの性質)を比べて,ウェッジ積は向きつき面積だと考えることが出来る,と(代数的な性質だけから)決めてしまいましたが,上述のようにテンソルとして見ることで,もう少しこのような見方の根拠が明確になったと思います. |
さて,一次微分形式の基底とも言うべき微小量 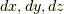 などは,重積分の変数変換の公式と同じように変換されるのでした.式
などは,重積分の変数変換の公式と同じように変換されるのでした.式  を再掲します.
を再掲します.
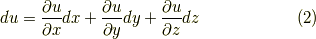
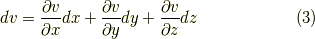
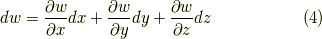
ここで, 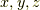 を
を 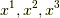 ,
, 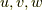 を
を 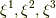 のように名前を付け直せば(座標変数の添字は右上に書くのが慣用でしたね),式
のように名前を付け直せば(座標変数の添字は右上に書くのが慣用でしたね),式  はまとめて次のように書けます.
はまとめて次のように書けます.

ここで 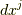 と
と  をベクトルと見れば, 共変ベクトルと反変ベクトル で考えたように,
をベクトルと見れば, 共変ベクトルと反変ベクトル で考えたように, 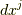 や
や  は 反変ベクトル だと考えることが出来ます.より高次の微分形式の基底(式
は 反変ベクトル だと考えることが出来ます.より高次の微分形式の基底(式 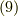 を見てください)も,やはり反変的に変換されることが分かります.さて,一般に
を見てください)も,やはり反変的に変換されることが分かります.さて,一般に 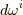 を
を 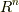 上の
上の 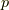 次微分形式の基底とすると(
次微分形式の基底とすると( 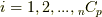 ),一般の
),一般の 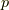 次微分形式
次微分形式 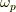 はこれらの線形結合として,次のように書けるでしょう.
はこれらの線形結合として,次のように書けるでしょう.

右辺は縮約になっており, 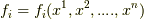 は関数です.ここで,ベクトル
は関数です.ここで,ベクトル  に着目すれば,
に着目すれば, 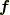 は共変ベクトルだと言えます.
は共変ベクトルだと言えます. 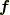 の各成分は
の各成分は 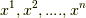 の関数で,場所によって値が変わりますから,より正確に言えば
の関数で,場所によって値が変わりますから,より正確に言えば 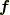 は 共変ベクトル場 です.もっと高次の微分形式は
は 共変ベクトル場 です.もっと高次の微分形式は 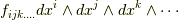 のように書けますが,それでもやはり
のように書けますが,それでもやはり 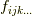 は 共変テンソル場 だと見ることが出来ます.このように,微分形式は共変テンソル場を表現する道具になっていることが分かりました.
は 共変テンソル場 だと見ることが出来ます.このように,微分形式は共変テンソル場を表現する道具になっていることが分かりました.
| [¶] | テンソルで最も本質的な性質と言えば,多重線形性ですが( 参考 ),微分形式ももちろん多重線形性を持ちます.微分形式の多重線形性は,微分形式をテンソルの一種と見れば明らかですし,ヤコビアン(より一般には行列式)の持つ多重線形性から考えても当然だと言えます.色々な見方が大事です. |