この記事は現在、プロジェクトメンバーによる査読中のものです。草稿段階ですので、内容・表現の正確さについて責任を負いかねます。
リンクを正しく張れていないところが存在しますのでご注意ください。
正式公開まで、いましばらくお待ちください。
複雑な回転を基本的な回転で表す方法
この記事では,座標系の回転に関する重要な定理を証明します.
今回の話から分かる事
ここに 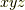 デカルト直交座標系(カーテシアン座標系とも言います)
と回転軸
デカルト直交座標系(カーテシアン座標系とも言います)
と回転軸 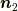 が有ったとします.それを別のある軸
が有ったとします.それを別のある軸  の周りに回転対象の点と座標軸を共に
の周りに回転対象の点と座標軸を共に 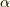 ラジアンだけ回転(この回転を
ラジアンだけ回転(この回転を  と書く事にします.)して,
と書く事にします.)して, 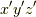 座標系の座標軸に移り
,
座標系の座標軸に移り
, 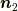 が
が 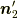 に移ったとします.
これと
に移ったとします.
これと 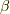 ラジアンの回転をする時,
ラジアンの回転をする時, 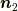 周りの回転
周りの回転 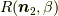 と,
と, 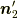 周りの回転
周りの回転 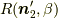 では結果は当然違いますが,
そこに単純なある関係があると言うものです.J.J.Sakuraiの『現代の量子力学(上)』(吉岡書店)に
この特別な場合が載っていますが,今回私はこの結果を拡張しました.
この記事でこれから扱うのは,座標系の中の点の「能動的回転」 [*] です.
ベクトル
では結果は当然違いますが,
そこに単純なある関係があると言うものです.J.J.Sakuraiの『現代の量子力学(上)』(吉岡書店)に
この特別な場合が載っていますが,今回私はこの結果を拡張しました.
この記事でこれから扱うのは,座標系の中の点の「能動的回転」 [*] です.
ベクトル  に回転
に回転  を作用させた結果を,
を作用させた結果を, 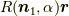 と書くと,
と書くと,
| [*] | : この回転は複素数平面での積をイメージして頂くのが一番です.  で実際に座標平面の上で点 で実際に座標平面の上で点 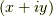 は回転します.「能動的回転」の対義語が「受動的回転」です.これは座標系とその中の点を考えた時,点は動かさないで,座標系の方を動かしてその座標を測りなおすと言うものです. は回転します.「能動的回転」の対義語が「受動的回転」です.これは座標系とその中の点を考えた時,点は動かさないで,座標系の方を動かしてその座標を測りなおすと言うものです. |
その定理とは,
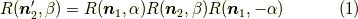
若しくは,
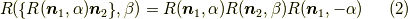
と言うものです.これが分かると,例えば以下の様なオイラー角の回転を直ぐに書き下せるようになります.
つまり, 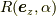 を行って
を行って 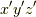 座標に移り,
次に
座標に移り,
次に 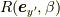 を行って
を行って 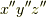 座標に移ります.
最後に
座標に移ります.
最後に 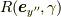 だけ回転します.これを
だけ回転します.これを 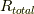 とします.
その時,回転は一番右から順に作用させるとすると,
とします.
その時,回転は一番右から順に作用させるとすると,
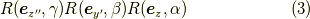
となりますが,回転後の軸周りの回転は煩わしいです. そんな時,この定理が使えて,
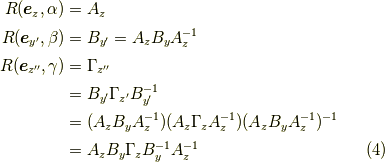
であります.
ここで 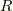 の逆回転を
の逆回転を 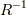 としました.
連続回転
としました.
連続回転 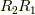 の逆は
の逆は 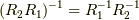 つまり,一つ目の回転をした後,
二つ目の回転を行った時,元に戻すには,二つ目の回転を逆に行い,一つ目の逆をすれば良いという事です.
よって,
つまり,一つ目の回転をした後,
二つ目の回転を行った時,元に戻すには,二つ目の回転を逆に行い,一つ目の逆をすれば良いという事です.
よって, 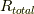 は
は
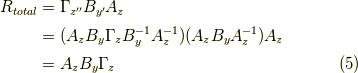
という結果が得られます.ここで, 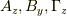 ならば簡単に書き下す事が出来て,
ならば簡単に書き下す事が出来て,

となります.今回の話のご利益はこんな感じです.では,式 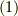 の証明に入りましょう.
の証明に入りましょう.
式(1)の証明
最初に回転軸 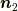 と
と 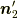 とは次の関係があります [†] .
とは次の関係があります [†] .
| [†] | : 回転の略記のRですが,ここまでの純粋に回転を表す記号から,以降では回転の行列を表しているとお考えください.この行列は直交行列であり,転置を 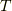 で表すと, で表すと,  であり, であり, 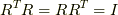 ( ( 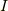 は単位行列)が成立します.つまり, は単位行列)が成立します.つまり, 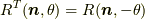 となります. となります. |

肝心の任意の回転軸周りの回転行列は,例えば
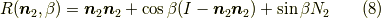
等となります.ここで  はダイアドであり,
はダイアドであり, 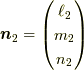 として,
として, 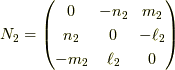 であり,任意の
であり,任意の  に掛かると,
に掛かると, 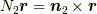 の様に外積に変化します.ちなみに,この記事で出てくる回転軸
の様に外積に変化します.ちなみに,この記事で出てくる回転軸 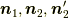 は全て長さが1です.(
は全て長さが1です.( 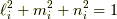 )また,ダイアドは,
)また,ダイアドは,  に対して,単なる行列積
に対して,単なる行列積 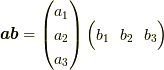 と言う行列だと思っておけば間違いが有りません.
と言う行列だと思っておけば間違いが有りません.
式 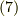 を使えば,
を使えば, 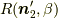 は変形できて,
は変形できて,
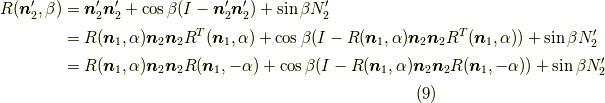
となります.ここで,
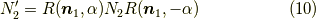
が示せれば,無事に
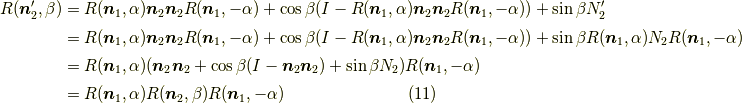
となります.よって,式 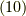 を示せば証明完了です.今回の話が成立すると確信を持った計算があります.
それは,次の必要条件を導いた計算です.式
を示せば証明完了です.今回の話が成立すると確信を持った計算があります.
それは,次の必要条件を導いた計算です.式 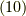 を辺々二乗したのです.
すると,
を辺々二乗したのです.
すると, 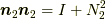 より,
より,

となり,矛盾しないからです.もちろん,  から
から  のみを導けないので,然るべき計算をこれから行います.
のみを導けないので,然るべき計算をこれから行います.
式(10)の証明
さて,  は
は 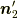 の成分を並べ替える事で手に入ります.
よって,まずは
の成分を並べ替える事で手に入ります.
よって,まずは 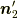 を求めましょう.式
を求めましょう.式 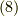 の添え字を
の添え字を 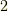 から
から 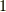 に変えたものを使って,
に変えたものを使って,
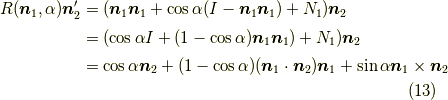
よって,この要素を並べ替えて出来る  は
は
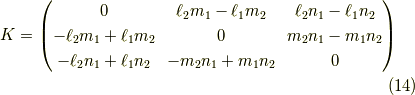
と言う行列 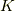 を使って,
を使って,

となります.ちなみに,
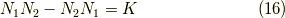
となっています.よって,我々は
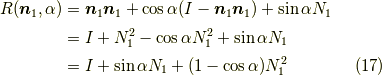
より,
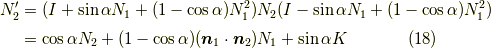
を示せばよいです.式(18)の中辺の計算を 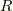 と置きます.
すると,
と置きます.
すると,

ここで,
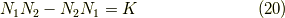
更に,

とすると,計算の後に

が分かります.また,

となります.ここから,
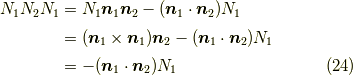
であります.

も言えます.
さて,これらを用いて式 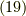 を変形していきます.
を変形していきます.
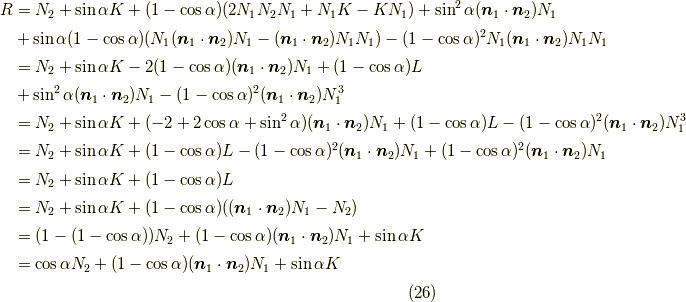
よって,無事に式  を示せました.
お疲れ様でした.それでは,今日はこの辺で.
を示せました.
お疲れ様でした.それでは,今日はこの辺で.